भौतिकी के मौलिक नियतांक भौतिकी में बहुत नियतांक ऐसे हैं, जिनके बारे में वैज्ञानिकों का ऐसा विश्वास है कि समय के साथ साथ उनमें कोई परिवर्तन नहीं होता। इन नियंताकों को भौतिकी के मौलिक नियतांक कहते हैं। हमारी चुनी हुई मौलिक इकाइयों के अनुसार इनका मान जो कुछ है, सर्वदा वही रहेगा। ऐसे नियतांकों के कुछ उदाहरण ये हैं: प्रकाश का वेग, अर्थात् वह वेग जिससे प्रकाश की तरंगों का संचरण शून्याकाश में होता है; इलेक्ट्रॉन का आवेश; सर्वव्यापी गुरूत्वाकर्षण का नियतांक, अर्थात् वह बल जिससे एक सेंटीमीटर की दूरी पर रखे एक ग्राम के दो पिंड एक दूसरे को आकर्षित करते हैं; ऊष्मागतिकी पैमाने पर बर्फ विंदु, अर्थात् बर्फ के पिघलने का ताप आदि।

इन नियतांकों का ठीक मान ज्ञात करने का प्रयत्न बहुत से वैज्ञानिक काफी दिनों से कर रहे हैं। सन् १९२९ के पहले प्रत्येक नियतांक को एक पृथक समस्या के रूप में ज्ञात किया जा रहा था। परंतु इन नियतांकों में आपस में संबंध होते हैं, जिनकी सहायता से इस बात की जाँच की जा सकती है कि इन नियतांकों के मानों में आपस में कोई असंगति दोष तो नहीं हैं। उदाहरणत:, प्रोटॉन का चुंबकीय आघूर्ण ^pP प्रयोगों द्वारा मापा जा सकता है। यह चुंबकीय आघूर्ण दूसरे नियतांकों द्वारा भी प्रकट किया जा सकता है, जिसका सूत्र है^श् pp =e h/p m_p C इसमें e, h, m_p तथा c, क्रमश: इलेक्ट्रॉन का आवेश, प्लांक नियतांक, प्रोटॉन की संहित एवं प्रकाश का वेग हैं। इन नियतांकों का मान भी प्रयोग द्वारा ज्ञात किया जा सकता है। चूँकि मापने में थोड़ी बहुत त्रुटि की संभावना है, इसलिये यह हो सकता है कि सूत्र में e, h, m_P तथा c का मान रखने पर जो संख्या प्राप्त हो, वह प्रयोग द्वारा ज्ञात किए गए pr के मान के बराबर न हो। इसलिये इन सभी नियतांकों का मान इस तरह निश्चित किया जाना चाहिए कि यह अंतर कम से कम हो। यहाँ पर इस आपसी संबंध का केवल एक उदाहरण दिया गया है। इसी तरह इन नियतांकों में और भी संबंध होते हैं।

इन परस्पर संबंधित नियतांकों में सबसे बड़ा समूह परमाणवीय नियतांकों का है। कुछ को छोड़कर लगभग सभी नियतांक इन्हीं नियतांकों द्वारा प्रकट किए जा सकते हैं। सबसे महत्वपूर्ण नियतांक, जो इनके द्वारा प्रकट नहीं किया जा सकता, गुरूत्वाकर्षण का नियतांक है। इन नियतांकों में से कुछ ऐसे मुख्य नियतांक चुने जाते हैं, जिनके द्वारा दूसरे नियतांकों को प्रकट किया जा सकता है। मान लीजिए ऐसे मुख्य नियतांकों की संख्या 'य' है। अब कुछ ऐसी मात्राएँ चुनी जाती हैं जिनका मान प्रयोग द्वारा बड़ी यथार्थता से मापा जा सकता है और जिन्हें इन चुने हुए मुख्य नियतांकों द्वारा प्रकट किया जा सकता है। ऐसी एक मात्रा का उदाहरण प्रोटॉन का चुंबकीय आघूर्ण हैं, जिसका जिक्र ऊपर किया गया है। इन चुनी हुई मात्राओं की संख्या कम से कम 'य' होनी चाहिए। पर यदि ऐसी चुनी हुई मात्राओं की संख्या 'य' से अधिक हो, तो हमारे पास इन नियतांकों का मान प्राप्त करने के लिये आवश्यकता से अधिक समीकरण होंगे। ऐसी दशा में यदि हम हिन्हीं 'य' समीकरणों में इनको रखें, तो हम देखेंगे कि गणना द्वाराश् प्राप्त किए गए मानों एवं प्रयोग द्वारा प्राप्त किए गए मानों में अंतर है। इसलिये हमें इन नियतांकों का वह मान ज्ञात करना चाहिए कि इन चुनी हुई मात्राओं के 'गणित मानों' एवं 'प्रायोगिक मानों' में न्यूनतम असंगति हो। इसके लिये इन नियतांकों के मान का निर्धारण 'न्यूनतम-वर्ग-रीति' द्वारा किया जाता है, तथा इसकी जाँच के लिये कि असंगति दोष न्यूनतम है, X¹ जाँच का उपयोग किया जाता है।

इन नियतांकों के मानों का विस्तृत विवेचन सबसे पहले बर्ज ने सन् १९२९ में किया। सन् १९३९ में डनिंगटन द्वारा किए गए अध्ययन के बाद से प्रति दूसरे अथवा तीसरे साल ऐसा अध्ययन किया जाता है। इन अध्ययनों में सबसे अच्छी बात यह हुई है कि इन नियतांकों का मान न केवल उत्तरोत्तर शुद्धता से ज्ञात किया जा सका है, अपितु यह भी हुआ है कि इनके नवीन मान पुराने निर्धारित मानों की त्रुटियों के अंतर्गत ही प्राप्त हुए हैं।

आगे ग्रामअणु, अथवा ग्रामतुल्यांक, के नियतांकों के मान भौतिकीय पैमाने में दिए हुए हैं। इस पैमाने में ऑक्सीजन के औ१६ (O^१६) समस्थानिक का परमाणवीय भार ठीक १६.०००००० माना जाता है। केवल इसी पैमाने में किसी संदेह की गुंजाइश नहीं होती। रासायनिक पैमाने में ऑक्सीजन के समस्थानिकों को लेकर,श् प्रकृति में पाए जाने वाले उनके अनुपात के अनुसार उनका औसत परमाणवीय भार निकाला जाता है और इस औसत भार को १६.०००० मानकर दूसरे नियतांक निर्धारित किए जाते हैं। परंतु नीर तथा दूसरों ने भारानुक्रमलेखी द्वारा जो बहुत ठीक ठीक प्रयोग किए हैं, उनसे यह असंदिग्ध रूप से निश्चित हो गया है कि ऐसा कोई अनुपात नहीं है जिसमें ऑक्सीजन के समस्थानिक प्रकृति में पाए जाते हैं। ऑक्सीजन का आ^ै१८ (O^१८) समस्थानिक के अनुपात का ४ प्रतिशत है।श् सन् १९५२ में फ्रेडरिक रोसिनी ने यह प्रस्ताव किया कि यह निश्चित हो जाना चाहिए कि भौतिकीय पैमाने के परमाणुभार में तथा रासायनिक पैमाने के परमाणुभार में क्या अनुपात है। सन् १९५२ में बर्ज ने यह मानकर कि प्रकृति में ऑक्सीजन के औ^१६ (O^१६) औ^१८ (O^१८)एवं औ^१७ (O^१७) समस्थानिक क्रमश: (५०६±१०),१ तथा (०.२०४ ± ०.००८) के अनुपात में पाए जाते हैं, यह निकाला था कि परिवर्तक गुणक (अर्थात् रासायनिक पैमाने के परमाणुभारों को जिस संख्या से गुणा करने पर भौतिकीय पैमाने के परमाणुभार ज्ञात होंगे) का मान १.०००२७२±०.०००००५ हैं, परंतु नीर ने यह दिखलाया कि इस गुणक का मान इस बात पर निर्भर करता है कि ऑक्सीजन किस स्रोत से प्राप्त किया गया है। नीर के अनुसार वायुमंडल के ऑक्सीजन के लिये इस गुणक का मान १.०००२७८श् तथा पानी के ऑक्सीजन के लिये इसका मान १.०००२६८ हैं। अब इसको १.०००२७५ मानने का प्रस्ताव है।

नीचे विद्युतीय राशियों को निरपेक्ष मानकों में दिखलाया गया है। निरपेक्ष स्थिरवैद्युत् मात्रकों के लिये e. s. u. एवं निरपेक्ष विद्युच्चुंबकीय मात्रकों के लिये e. m. u.लिखा गया है। e v इलेक्ट्रॉन वोल्ट का द्योतक है। यह इलेक्ट्रॉन की वह गतिज ऊर्जा है, जो उसे एक वोल्ट के विभव में चलने से प्राप्त होती है।

१.      सहायक नियतांक- ये वे नियतांक हैं जिनके मान स्वतंत्र प्रयोगों द्वारा इतनी शुद्धता से ज्ञात है कि इनका मान न्यूनतम वर्ग रीति द्वारा निर्धारित नहीं किया जाता है, पर इनका उपयोग दूसरे नियतांकों का मान निर्धारित करने के लिये किया जाता है। प्रत्येक संख्या के बाद ± चिन्हों के साथ जो राशि लिखी गई है, वह मानों में प्रामाणिक त्रुटि है

रिडवर्ग संख्या (अनंत संहति के लिये):

R_¥= (१०९७३७.३०९± ०.०१२) सेंमी-^१।

न्यूट्रॉन की परमाण्वीय संहति:

श्n=१.००८९८२± ०.०००००३(भौतिकीय पैमाना)।

हाईड्रोजन की परमाणवीय संहति:

H=१.००८१४२ ± ०.०००००३ (भौतिकीय पैमाना)।

डयूटीरियम की परमाणवीय संहति:

D = २.०१४७३५±०.०००००६ (भौतिकीय पैमाना)।

हीलियम^४ की परमाणवीय संहति:

He = ४.००३८७३± ०.००००१५ (भौतिक पैमाना)।

गैसनियतांक (प्रतिमोल-भौतकीय पैमाना):

R₀ = (८.३१६९६±०.०००३४).१०^८ अर्ग मोल-^१ डिग्री-^१ (भौतिक पैमाना)।

आदर्श गैस का प्रामाणिक आयतन (भौतिकीय पैमाना):

V₀ = (२२४२०.७±०.६) सेंमी^३ वायुमंडल प्रति मोल (भौतिकीय पैमाना)।

गुरूत्वाकर्षण नियतांक:

G = (६.६७०±०.००५) x १०^-८ श्डाइन सेंमी^२ ग्राम-^२।

प्रामाणिक वायुमंडल (परिभाषा):

A₀ =१.०१३२५०.०० डाइन सेंमी^-२ वायुमंडल^-९।

हिमबिंदु:

T0 =२७३ १५०० ± ०.०००२^० परम

जूल तुल्यांक (परिभाषा):

J = ४.१८४० जूल प्रति ऊष्मागतिकीय कैलोरी।

जूल तुल्यांक (प्रायोगिक १५^० कैलोरी):

J_१५ = ४.१८५५ ± ०.०००४ जूल प्रति १५^० कैलोरी।
प्रकाश की गति:

c = (२९९७३.० ± ०.३) किमी० सेकंड^-१

२. न्यूनतम वर्ग रीति से निर्धारित मान (प्रत्येक संख्या के साथ ±चिन्हों के बाद की राशि प्रामाणिक त्रुटि की द्योतक है)- आवोगाड्रो संख्या, अर्थात प्रति मोल अणुओं की संख्या (भौतिकीय पैमाना):

N = (६.०२४८६±०.०००१६).१०^२३ मोल^-१

ल संख्या (भौतिकीय पैमाना):

L₀ =N/V₀ = (३.६८७१९±०.०००१०). १०^१२ सेंमी.^-३।

इलेक्ट्रॉन का आवेश:

e =  (4.802286 ± 0.00009).10^-10 e.s.u.

e¢= e/c = (१.६०२०६±०.००००३) x१०^-२० e. m.u.

इलेक्ट्रॉन की संहति:
m= (९.१०८३±०.०००३). १०^-२८ ग्राम।

प्रोटोन की संहति (जब प्रोटॉन निश्चल हो)

m_p = M_p/N= (१.६७४७०±०.००००४). १०^-२४ ग्राम।

निश्चल न्यूट्रॉन की संहति:

m_n = n/N = (१.०५४४३±०.००००४).१०^-२४ ग्राम।

प्लांक का नियतांक:

h = (६.६२५१७±०.०००२३).२३^-२७अर्ग सेकंड।

h = h/2p = (१.०५४४३±०.००००४).१०^-२७ अर्ग सेकंड।

फैराडे नियतांक (भौतिकीय पैमाना):

F = Ne = (२.८९३६६ ±०.००००३).१०_१४ e. s. u. मोल^-१।

F¢= Ne/c = (९६५२.१९±०.११) e. m. u ^१ मोल^१ ।

इलेक्ट्रॉन के आवेश एवं संहति का अनुपात:

e/m = (५.२७३०५±०.००००२).१०^७ e.s.u.ग्राम^-१

e¢/m = e/mc = (१.७५८९०±०.००००२).१०^७ e. m. u. ग्राम^-१

सूक्षम संरचना नियतांक:

hc/e² =1/a =137.0373±0.0006।

इलेक्ट्रॉन की परमाणवीय संहति (भौतिकीय पैमाना):

Nm = (5.48763±0.00006).10^-8।

प्रोटॉन एवं इलेक्ट्रॉन की संहति का अनुपात:

M_p/Nm =1836.12±0.02

बोर की प्रथम परमाण्वीय कक्षा की त्रिज्या:

a₀ = h²/me² = (5.29172±0.00002).10^-9 सेंमी.

इलेक्ट्रॉन का कांपटन तरंगदैर्ध्य:

l₀₀ = h/mc =(24.2626±0.0002).10^-11सेमी.

इलेक्ट्रॉन की त्रिज्या (चिरसंमत भौतिकी के अनुसार):

r₀ =e₂/ mc² = (2.51785±0.00004).10^-13 सेमी.

बोल्ट्समान का नियतांक:

 K = R₀/N= (1.38044± 0.00007) x10^-16 अर्गप्रति डिग्री

= (8.6167± 0.0004) x 10^-5 ev प्रति डिग्री।

प्लांक के विकिरण नियम से संबंधित राशियाँ, जो कृष्ण पिंड के विकिरण के सूत्र में आती हैं:

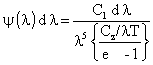
विकिरण का प्रथम नियतांक:

C₁ = 8 ph c = (4.9918± 0.0002).10^-15 अर्ग सेंमी०

विकिरण का द्वितीय नियतांक:

C₂ =h c/k= (1.43880 ± 0.00007) सेंमी० डिग्री।

बियेन का विस्थापन नियतांक:

l_max T = (0.289782 ± 0.000013) सेंमी. डिग्री।

स्टीफान-बोल्ट्समान नियतांक:

०^- = (0.92731 ± 0.00002) .10^-4 अर्गसेंमी^-२ डिग्री^-४ सेंकड़^-१।

बोर मैग्नेटॉन:

m₀  (0.92731 ± 0.00002) + 10^-20 अर्गप्रति गाउस।

इलैक्ट्रॉन का चुंबकीय घूर्ण:

m_e  = (0.92837 ± 0.00002)0.10^-20 अर्ग प्रति गाउस।

नाभिकीय मैग्नेटान:

m_n  = (0.505038 ± 0.000018).10^-23 अर्ग प्रति गाउस।

प्रोटॉन का घूर्ण :

m_p  = (2079275± 0.000003) नाभिकीय मैग्नेटान।

  = (1.741044 ± 0.00004).10^-23 अर्ग प्रति गाउस।

इलेक्ट्रॉन की ब्रॉग्ली तरंगदैर्ध्य :

l_De  = (1.552257± 0.000016).10^-13 सेंमी. (अर्ग)^१/२/E^1/2

(इलेक्ट्रान की ऊर्जा (E)अंगों में है)

हाइड्रोजन का आयनीकरण विभव:

I₀ = 13.59765 ± 0.00022) ev

सं०ग्र० - डुमांड तथा ई० आर० कोहेन: रिपोर्ट टु नैशनली रिसर्च कौंसिल कमिटी ऑन कॉन्सटैंट्स ऐंड कनवर्ज़न फैक्टर्स इन फिज़िक्स,श् दिसंबर १९५०; जे० ए० बीर्डेन तथा जे० एस० टामसेन: नूवो सिमेंटो,

५, २६७, १९५७; ई० आर कोहेन, नूवो सिमेंटी, ६,११०,१९५७; आर० डी० हुंटून तथा ए० जी० मैकनीश : नूबो सिमेंटो,

६, १४६, १९५७ । [रामनिवास राय]