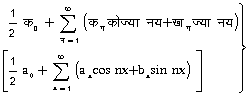
फ़ूर्ये श्रेणी हम सबसे पहले निम्नलिखित अनंत श्रेणी

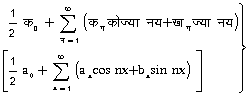
. . . . . . . . . (१)

पर विचार करेंगे, जिसमें सभी क (a) और ख (b) अचर है और य (x) चर है जो -्ब्र और अ्ब्र के बीच का कोई भी मान ले सकता है। ऐसी श्रेणियों को त्रिकोणमितीय श्रेणियाँ कहते हैं। मान लीजिए, अब श्रेणी (१) य (x) के सब मानों के लिए अभिसृत होती है और इसका योग फ (य) [f (x)] है। चूँकि य (x) के बदले (यअ२द्र) [(x+2द्र)] रखने पर श्रेणी में कोई अंतर नहीं आता, इसलिए फलन फ (य) [f (x)] आवर्तं है, जिसका आवर्तनांक २द्र है। यदि हम समीकरण

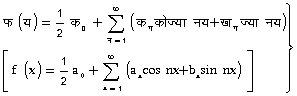
के दोनों पक्षों को क्रमश: कोज्या नय (cos n x) या ज्या नय (sin n x) से गुणा करें और फल का (0, 2द्र) अंतराल पर समाकल निकालें तो न (n) के सभी मानों के लिए हमें निम्नलिखित समीकरण प्राप्त होता है:

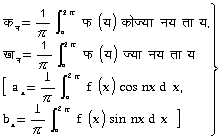. . . . . . . . . (२)

समीकरण (२) फलन फ (य) [f (x)] के फूर्ये गुणांक कहलाते हैं और श्रेणी (१) फ (य) [f (x)] की फ़ूर्ये श्रेणी कहलाती है।

यदि श्रेणी (१) एकरूपत: अभिसृत हो, तो उपरिलिखित तर्क सत्य प्रमाणित हो जाता है। फ्रांस के गणितज्ञ ज़्हाँ बातीस्त फ़ूर्ये (Jean Baptiste Fourier) के नाम पर इस श्रेणी का नामकरण हुआ है। फूर्ये का ''ताप की चाल का गणितीय सिद्धांत'' भी इन्हीं श्रेणियों पर आधारित है। फूर्ये का अनुसंधानपत्र ''ऊष्मा का वैश्लेषिक सिद्धांत'' (Theorie Analytique De La Chaleur) सन् १८२२ में प्रकाशित हुआ था, परंतु फ़ूर्ये श्रेणी का आविष्कार अट्ठारहवीं शताब्दी के पूर्वार्ध में कंपमान डोरी के प्रश्न के साथ ही हो गया था। इस प्रकार फूर्ये श्रेणी का प्रारंभ गणितीय भौतिकी के प्रश्नों से हुआ और यह श्रेणी अब तक इसके लिए एक महत्वपूर्ण कड़ी बनी हुई है। वास्तव में फलन को ज्याओं (sines) और कोज्याओं (cosines) की श्रेणी में प्रसारित करके, सम्मिश्र असतत फलनों का मान निकालने के लिए यह श्रेणी एक गणितीय युक्ति है, जिसके गुणांक प्राय: समाकलन करके परिकलित किए जाते हैं और इस प्रकार प्रसार निर्धारित होता है। ज्वार भाटे से सहचरित आवर्त फलनों के हल, वैद्युतीय धारा, वोल्टता, ताप का अंतरण, संभवित के सिद्धांत और आंशिक अवकल समीकरण, तरंगगति का सिद्धांत, (उदाहरणार्थ प्रकाश और ध्वनितरंगों की गतियों के सिद्धांत,) तथा दोलक यांत्रिक संहति, जैसे कंपमान डोरी, और खगोलीय कक्षाओं आदि, में फ़ूर्ये श्रेणी बहुधा प्रयुक्त होती है।

गणितीय विश्लेषण में भी फूर्ये श्रेणी का उतना ही महत्व है। त्रिकोणमितीय (और विशिष्ट रूप से फूर्ये) श्रेणियाँ वैश्लेषिक फलनों के सिद्धांत के लिए विशेष रूप से महत्वपूर्णं हैं, क्योंकि लउघ^रय [Z=e^ix] रखने पर घात श्रेणी

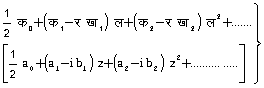. . . . . . . . . (३)

का वास्तविक अंश ही श्रेणी (१) हो जाता है। इस प्रकार त्रिकोणमितीय श्रेणियाँ घात श्रेणियों की वास्तविक अंश हैं और इसलिए ये वास्तविक तथा संमिश्र फलनों की बीच एक शृंखला का काम करती हैं। विविध गणितीय संकल्पनाओं के, जिनमें से कुछ काफी अमूर्तं हैं, ऐतिहासिक विकास और स्पष्टीकरण में त्रिकोणमितीय श्रेणियों ने बड़ा महत्वपूर्ण योगदान किया है। नीचे कुछ उदाहरण दिए गए हैं।

अट्ठारहवीं शताब्दी के प्रारंभिक काल में ही फूर्ये श्रेणी के सिद्धांत ने गणितीय फलनों की संकल्पना के बारे में विवाद खड़ा कर दिया। साधारणतया उन दिनों फ (य) [f (x)] को फलन तभी कहा जाता था, जब फ (य) [f (x)] बहुपद, जैसे एक एकाकी वैश्लेषिक व्यंजक, एक घात श्रेणी या एक त्रिकोणमितीय श्रेणी के रूप में निरूपित हो सकता हो। यदि फ (य) [f (x)] का आलेख स्वेच्छ होता था, जैसे एक बहुपदीय रेखा, तो फ (य) [f (x)] को फलन नहीं मानते थे। इसलिए बहुतों को आश्चर्यं चकित रह जाना पड़ा, जब फूर्ये श्रेणी के आविष्कार ने सिद्ध कर दिया कि ऐसे बहुत से स्वेच्छ आलेख त्रिकोणमितीय श्रेणियों के द्वारा निरूपित हो सकते हैं और इसलिए इन्हें फलन स्वीकृत किया जाना चाहिए। लंबे काल के बाद ही इसका पूर्णरूपेण स्पष्टीकरण हो पाया और डीरिक्ले (Dirichlet) द्वारा सन् १८३७ में प्रकाशित एक गवेषण लेख में नई सर्वमान्य परिभाषा का सर्वप्रथम सूत्रपात हुआ, जिसमें फूर्ये श्रेणी का विवेचन किया गया था। त्रिकोणमितीय श्रेणी के प्रयाग के दूसरे उदाहरण के रूप में हम वायरश्ट्रास (Weierstrass) के फलनों का सिद्धांत ले सकते हैं। इन्होंने पहली बार एक त्रिकोणमितीय श्रेणी के रूप में एक ऐसे सतत फलन का उदाहरण दिया, जो किसी बिंदु पर भी अवकलनीय नहीं था। समाकलों की संकल्पना के इतिहास में फ़ूर्ये श्रेणी का प्रभाव एक तीसरा महत्वपूर्ण उदाहरण है। समीकरण (२) के कारण फूर्ये श्रेणी के अध्ययन के लिए समाकलों का ज्ञान पहले से ही होना आवश्यक है। इस कारण यह ध्यान देने येग्य बात है कि रीमान (Riemann) द्वारा समाकल की शास्त्रोक्त परिभाषा सन् १८५४ में उसके मूल आलेख ''किसी फलन की त्रिकोणमितीय श्रेणी द्वारा निरूपणशीलता'' (Veber die Darstellbarkeit einer Funcktion durch eine Trigonometrische Reihe) में प्रतिपादित हुईं। एक त्रिकोणमितीय श्रेणी के एक फलन के रूप में निरूपण की अद्वितीयता पर जार्ज कांटर (George Cantor) का एक फल भी इस आलेख द्वारा बहुत प्रभावित होता है।

फूर्ये श्रेणी की अभिसृति और अपसृति - मान लीजिए, श्रेणी (१) के प्रथम (नअ१) [(n+1)] पदों का योग यो_न (य) [S_n (x)] है। समीकरण (२) को प्रयोग में लाने से हमें फूर्ये श्रेणी के लिए आधारभूत सूत्र

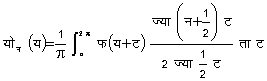
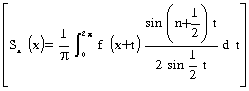
प्राप्त होता है। अब कुछ शर्तों के साथ यह सिद्ध किया जा सकता है कि यो_न (य) [S_n(x)], फ (य) [f (x)] की ओर प्रवृत्त होगा, यदि न (n) अनिश्चित रूप से बढ़े। ऐसे बिंदु य (x) पर, जहाँ फलन फ (य) [f (x)] असतत हो, फूर्ये श्रेणी अभिसृत होती है और उसका योग

फ (यअ०) अफ (य-०)

[ f (x+0)+f(x-0)]

होता है जिसमें फ (यल्०) [f (xल्0)], फलन फ (य) [f (x)] की क्रमश: दाएँ और बाएँ से बिंदु य (x) पर सीमाएँ हैं। फूर्ये श्रेणी का योग फ (य) [f (x)] की ओर अभिसृत होने के लिए एक दूसरी शर्त है समाकल

का अभिसृत होना। यह शर्त प्रत्येक ऐसे बिंदु पर सत्य होगी, जहाँ फलन फ (य) [f (x)] अवकलनीय हो। ये शर्तें पर्याप्त मात्र हैं। सन् १८७२ में पॉल ड ब्वा-रेमाण्ड (Paul de Bois-Reymond) ने एक ऐसे सतत फलन की रचना की जिसकी फूर्ये श्रेणी कुछ विंदुओं पर अपसृत होती है और इस प्रकार यह सिद्ध हो जाता है कि फूर्ये श्रेणी की अभिसृति के लिए फलन का सातत्यमात्र ही पर्याप्त नहीं है। सन् १९२६ में कॉलमॉगोरॉफ (Kolmogoroff) ने ऐसे फलोंन का अस्तित्व सिद्ध किया जो लेबेग (Lebesgue) अर्थ में समाकलनीय हैं, किंतु जिनकी फूर्ये श्रेणी सर्वत्र अपसृत होती है।

फूर्ये श्रेणी की संकलनीयता - सन् १९०० में फेयर (Fejer) ने संख्यात्मक मध्यकों के द्वारा यह दिखाया कि एक सतत फलन फ (य) [f (x)] की फूर्ये श्रेणी का संकलन फल फ (य) [f (x)] है। यदि हम यो_न (य) [S_n(x)] का पूर्व परिभाषित अर्थ लें तो

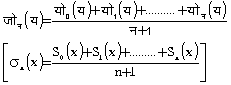
फलन के प्रत्येक सातत्य बिंदु पर फ (य) [f (x)] की ओर प्रवृत्त होगा। बाद में लेबेग ने सिद्ध किया कि प्रत्येक समाकलनीय फलन फ (य) [f (x)] के लिए व्यंजक जो_न (य) [द्म_n(x)] प्राय: सर्वत्र फ (य) [f (x)] की ओर प्रवृत्त होता है। इस प्रकार स्पष्ट है कि फूर्ये श्रेणी की संकलनीयता उसकी अभिसृति से अधिक महत्वपूर्ण है।

पार्सेवाल (Parseval) का सूत्र - यदि हम समीकरण

के दोनों पक्षों का वर्ग करें और फल का ०फ्रयफ्र२द्र ([0फ्रxफ्र2द्र]) अंतराल में समाकल निकालें तो हमें पार्सेवाल का सूत्र

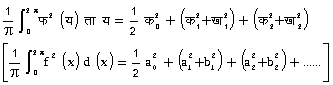
प्राप्त हो जाता है। इस फल की परुष उपपत्ति से ज्ञात होता है कि यह सूत्र ऐसा सभी फलनों फ (य) [f (x)] के लिए सत्य है, यदि फ^२ (य) [f² (x)] समाकलनीय हो। इस प्रकार यह सिद्ध होता है कि फूर्ये गुणांक क_०, क_१, ख_१,...... [a₀, a₁, b₁,.....] ऐसे हैं कि च्(क_न^२अख_न^२) [च्(a_n²+b_n²)] सांत हैं। रीज़ (Riesz) और फिशर (Fischer) के प्रमेय के अनुसार, यदि किन्हीं संख्याओं क_०, क_१, ख_१,...... का अनुक्रम दिया हो और श्रेणी च्(क_न^२अख_न^२) अभिसृत होती हो, तो सदैव एक ऐसा फलन फ (य) [f (x)] प्राप्त किया जा सकता है जिसके फूर्ये गुणांक, संख्याएँ क_०, क_१, ख_१,....... हों और फ^२ (य) [f²(x)] समाकलनीय हो। यह फलन अद्वितीय है।

फ़ूर्ये के समाकल - फूर्ये श्रेणी का उपयोग आवर्त फलनों के निरूपण के लिए किया जाता है। अनावर्त फलन फ (य) [f (x)] के अध्ययन के लिए हम फूर्ये समाकल

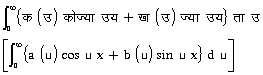
का उपयोग करते हैं, जिसमें क (उ) [a (u)] और ख (उ) [b (u)] निम्नलिखित सूत्रों द्वारा परिभाषित होते हैं:

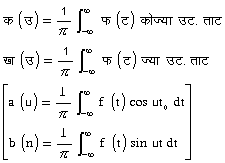
क (उ) और ख (उ), फ (उ) के फूर्ये रूपांतर कहे जाते हैं। (भगवानदास अग्रवाल.)