द्रव्य का गत्यात्मक सिद्धांत (Kinetic Theory of Matter) द्रव्य की ठोस, द्रव तथा गैस, तीन अवस्थाएँ होती हैं। गत्यात्मक सिद्धांत के अनुसार द्रव्य किसी भी अवस्था में अणुओं से भरा हुआ होता है। ये अणु समस्त दिशाओं में इतस्तत: घूमते रहते हैं और इनमें स्थिरता कभी भी नहीं होती। इन अणुओं का चलन तथा क्रिया अभिक्रिया, ताप और दाब पर निर्भर होती है। ठोस द्रव्य, जिसपर बाहर की दाब नहीं है, अपना आकार सर्वदा अचल रखता है। इसका अर्थ यह है कि ठोस द्रव्य के अणु किसी मध्यमान, संतुलन स्थिति के आस पास दोलन करते रहते हैं और यह दोलन अति मंद होता है। द्रव अवस्था में अणुओं को इधर उधर घूमने में अधिक सरलता होती है। तथापि ठोस अथवा द्रव अवस्था में अणुओं का परस्पर अंतर बहुत कम होने के कारण इनकी क्रिया प्रतिक्रिया बहुत होती है, ये संपीडन का विरोध करते हैं और इनमें संसजन होता है। द्रव अवस्था में अणुओं के सरलता से इधर उधर घूम सकने के कारण द्रव वस्तु का आकार सुगमता से बदल सकता है। गैस अवस्था में द्रव के अणु इतस्तत: विशेष सरलता से घूमते हैं और इनमें क्रिया प्रतिक्रिया की संभावना बहुत कम होती है। इनका संसजन अति सूक्ष्म होता है। जिस बर्तन में गैस भरा होती है। इनका संसजन अति सूक्ष्म होता है। जिस बर्तन में गैस भरा होता है उस वर्तन की दीवारों पर गैस के अणु टकराते हैं और इस कारण इनकी गति में परिवर्तन होता रहता है। इन टक्करों से गैस का दाब उत्पन्न होता है। गैस का अवकाश में फैलना तथा एक गैस का दूसरी गैस में फैल जाना अणुओं की स्वतंत्रता पर निर्भर है। इस स्वतंत्रता के कारण ठोस तथा द्रव के सपेक्षतया गैस का गत्यात्मक सिद्धांत अधिक विकसित हुआ। इस सिद्धांत के अनुसार ऊष्मा केवल यांत्रिक ऊर्जा है। हम जानते हैं कि गैस के एक स्वतंत्र अणु का चलन हम देख नहीं सकते और एक स्वतंत्र अणु का गुण हमें ज्ञात नहीं होगा। जो गुण हमें ज्ञात होते हैं, वे अणुओं के एक समुच्चय की क्रियाओं के मध्यमान गुण हैं। इस परिस्थिति में हमें मध्यमान फल ज्ञात करने की आवश्यकता होती है। हम जितने फल ज्ञात करते हैं वे सब संभाविकी तथा सांख्यिकी के सिद्धातों पर निर्भर होते हैं।

गैस के विषय में जितने प्रयोग किए गए उनमें बॉयल (Boyle) और मैरीऑट (Mariotte) नामक वैज्ञानिकों के प्रयोग बहुत प्राचीन हैं। उन्होंने गैस की संपीड्यता के नियम निर्धारित किए। सन् १७३० में बेर्नुलि (Bernoulli) ने अणुओं की गति द्वारा बॉयल के सिद्धांत की व्याख्या की। १९वीं शताब्दी में डाल्टन आवोगाद्रो तथा गेत्यूसक ने अपने आविष्कारों तथा अन्वेषणों से अणु संबंधी बहुत सी बातों पर महत्वपूर्ण प्रकाश डाला। मेक्सवेल (Maxwell) और क्लॉसिअस (Clausius) ने अणु सिद्धांत की नींव गणित की सहायता से पक्की कर दी। इसके अनंतर बोल्ट्समान (Boltzman), किर्खाफ़ (Kirchhoff), वान डर वाल (Van der waal), लार्ड रैलि (Lord Rayleigh) तथा लारेंट्स (Lorentz) ने सैद्धांतिक क्षेत्र में इतनी विशाल प्रगति की कि द्रव्य का गत्यात्मक सिद्धांत भौतिक विज्ञान की एक महत्वपूर्ण शाखा बन गया।

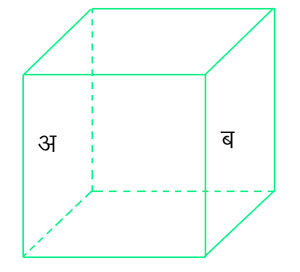
चित्र १.

गैस की दाब - एक घनाकार पोला बक्स लें जैसा चित्र १. में दिखाया गया है। मान लें, इस बक्स का आयतन आ (v) है तथा बक्स में स्थित अणुओं की संख्या सं (N) है। प्रत्येक अणु बहुत वेग से चलता है और ये सब अणु लचीले अर्थात् प्रत्यास्थापक हैं। इस कारण ये दीवारों से टकराकर उछलते हैं। सूक्ष्म होने के कारण अपनी यात्रा में यह परस्पर बहुत कम टकराते हैं और इस कारण अपनी चर्चा में हम इनकी टक्करों का विचार नहीं करेंगे। मान लें एक अणु वे_१ (V₁) वेग से बक्स के अ पृष्ठ से समकोण रेखा में टकराता है। यदि अणु का द्रव्यमान द्र (m) है, तो अणु के टकराने का संवेग द्र वे_१ (mV₁) होगा। अ पृष्ठ से परावर्तित होकर अणु ब पृष्ठ की ओर जाता है। परावर्तन की स्थिति में अणुसंवेग + द्र वे_१ (+mV₁) से - द्रवे_१ (- mV₁) होता है। इस कारण संवेग का संपूर्ण परिवर्तन २ द्र वे_१ (2mV₁) होगा। अ पृष्ठ से परावर्तित होकर, अणु व पृष्ठ से टकराता है और वहाँ से फिर अ पृष्ठ पर गिरता है। इस प्रकार आघात होते रहते हैं। अ और ब पृष्ठ के बीच का अंतर यदि ल (l) है, तो अ पृष्ठ से परावर्तित होकर पुन: अ पृष्ठ पर आने में अणु को 2 ल (2 l) अंतर चलना होगा। वे_१ (V₁) वेग के कारण प्रत्येक सेकंड में वे_१/२ल (V₁/2l) आघात होंगे। प्रत्येक आघात के समय संवेग में २द्र वे_१ (2mV₁) परिवर्तन होने के कारण अ पृष्ठ पर प्रति सेकंड संवेग का परिवर्तन

होगा। इसी प्रकार अन्य अणु, जो क्रमश: वे_२ (V₂), वे_३ (V₃) इत्यादि वेगों से अ पर आघात करते हैं, वे संवेग में परिवर्तन करेंगे। सब परिवर्तनों का योग

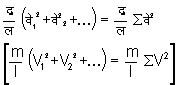
होगा। इन सब संवेगों के कारण अ पृष्ठ पर द्र/लें �वे^२ (m/l � V²) बल उत्पन्न होगा। पृष्ठ के क्षेत्रफल से बल को भाग देने से दाब ज्ञात होगी। इसलिए अ पर दाब

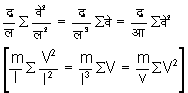
होगी। यदि धन के पृष्ठों की शेष दो जोड़ियों पर अणु म (U) और ग (W) वेगों से आघात करते हों, तो उन पृष्ठों पर और दाब होगी। सब दाब समान होने की पायिकता होने के कारण

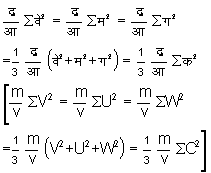
जहाँ क^२= (वे^{२ +} म^{२ +} ग^२) [C²=V²+U²+W²]*

अत: जब अणुओं की संख्या सं (N) है, तो प्रत्येक पृष्ठ पर दाब

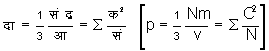
होगी। सब अणुओं के वेगों के वर्ग का मध्यमान मूल्य चिन्ह से दिखाएँ तो � क^२/सं (� C²/N) के स्थान पर / लिखकर

हमें

समीकरण प्राप्त होता है। यहाँ को मध्यमान वर्ग वेग (mean square velocity) कहते हैं। अणुओं का चलन ताप पर निर्भर करता है। अत: परम ताप (absolute temperature) टा (T) का अनुक्रमानुपाती होगा।

दा आ = 1/3 सं द्रटा नि (p v=1/3 N m T K), जहाँ नि (K) एक स्थिरांक है।

१/३ सं द्र नि = थ (1/3 N m K=R) रखकर हम देखते हैं कि दा आ = थ टा (pv=RT)

इस समीकरण को बॉयल का नियम कहते हैं। यहाँ थ (R) को गैस का स्थिरांक (gas constant) कहते हैं। सं द्र/आ = घ [Nm/v=r ], जहाँ घ (r ) घनत्व है। इसलिए दा = 1/3 घ [p=1/3 r ]। गैस की दाब तथा घनत्व प्रयोग द्वारा ज्ञात हो सकने के कारण हम भिन्न भिन्न गैसों के अणुओं के वेग निर्धारित कर सकते हैं। कुछ गैसों के लिए हम वेग के मूल्य तथा थ/द्र (R/m) के मूल्य यहाँ सारणी में देते हैं :

गैस		ताप सेंटीग्रेड में	वेग प्रति सेकंड (मीटर में)
हाइड्रोजन	४१३० � १०४	०� - २५३�	१८३९ ४८९
हीलियम	२०९८ � १०४	०�	१३११
पानी की भाप	४६२ � १०४	०� १००�	६१५ ७१९
कार्बन मोनॉक्साइड	२९६ � १०४	०�	४९३
नाइट्रोजन	२९५ � १०४	०�	४९२
हवा	२८७ � १०४	०�	४८५
ऑक्सीजन	२६० � १०४	०� - १८२.५�	४६१ २६६
आर्गन	२०९ � १०४	०�	४१३
कार्बंन डाइऑक्साइड	१८९ � १०४	०�	३९३
पारा	४१६ � १०४	०�	१८५

वान डर वाल का समीकरण - बॉयल के नियमानुसार ताप को अचल रखकर गैस की दाब को घटाने बढ़ाने से गैस का आयतन इस प्रकार बढ़ता घटता है कि दाब और आयतन का गुणनफल स्थिर रहता है। ऐसा देखा गया है कि बायल का नियम कुछ सीमा तक ही सही होता है। दाब में बहुत वृद्धि करने से तथा ताप बहुत कम करने से इस नियम में त्रुटि होगी। इस त्रुटि का कारण ढूँढने का पहले पहल प्रयत्न वान डर वाल ने किया और बायल के समीकरण का संशोधन किया। इस संशोधित समीकरण को वान डर वाल का समीकरण में अधिक संशोधन किया और एक ऐसा समीकरण ज्ञात किया जिसमें कम दाब से बहुत उच्च दाब तक तथा बहुत कम ताप से उच्च ताप तक यथार्थता बनी रहती है। बॉयल का नियम निश्चित करने में य मान लिया गया था कि अणु का आयतन उपेक्षणीय है, किंतु अणुओं का आयतन अवश्य है। इस कारण आ (v) आयतन के बरतनों में अणुओं को इधर उधर घूमने के लिए आ (v) आयतन की जगह केवल आ - ब (v- b) आयतन मिलता है। यहाँ ब (b) स्ामस्त अणुओं का आयतन है। बरतन की दीवारों पर अणुओं की दाब केवल उनके टकराने से नहीं पड़ती। इस क्रिया के अतिरिक्त अतंराणुक (Intermolecular) आकर्षण के कारण भी दाब उत्पन्न होती है। दीवारों के निकट इस आकर्षण का प्रभाव बहुत होता है। शेष अणुओं के आकर्षण का योग शून्य होता है। अणुओं का आकर्षण उनके घनत्व का अनुक्रमानुपाती होता है। इस कारण प्रत्येक अणु का घनत्व यदि घ (r ) हो, तो यह आकर्षण ग घ^२ (a r ²) किंवा ग/आ^२ (a/v²) होगा। यहाँ ग (a) अनुपातिता गुणांक (coeffecient of proportionality) है। अत: वास्तविक दाब दा + ग/आ^२ (p+ a/v²) और आयतन आ - ब (v- b) है, यह ज्ञात हुआ तथा वान डर वाल का समीकरण

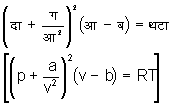
प्राप्त हुआ।

अणु का परिणामित वेग - हमने सारणी में देखा है कि अणु का वेग बहुत अधिक होता है, परंतु अणुओं के परस्पर टकराने के कारण किसी एक अणु का परिणामित वेग बहुत कम हो जाता है।

अणु का मध्यमान मुक्त पथ (mean free path) - दो टक्करों के बीच के समय में अणु जितना अंतर अतिक्रमण करता है, उस अंतर को अणु का मध्यमान मुक्त पथ कहते हैं। यहाँ हम कल्पना करेंगे कि अणुओं में परस्पर आकर्षण शून्य है और अणुओं का आकार गोलियों के भिन्न भिन्न दिशाओं के वेगों के किसी निश्चित दिशा में विश्लेषित पटक लें, तो ये देखा जाता है कि एक विशिष्ट अंतर प (L) के अनंतर विश्लेषित घटकों का मध्यमान मूल्य कम होता है, अर्थात् प (L) अंतर चलने के पश्चात् उस दिशा में चलनेवाले अणुओं की मध्यमान संख्या कम हुई। इस प (L) अंतर से हमें अणुओं का मध्यमान मुक्त पथ ज्ञात होता है और हमें अणुओं की रचना अथवा अणुओं के बीच के आकर्षण का विचार करने की आवश्यकता नहीं होती। अणु का व्यास क (d) माना, तो जिस समय दो अणु परस्पर टकराएँ उस समय अणुओं के केंद्र में क (d) अंतर होगा। एक सेंटिमीटर अंतर अतिक्रमण करने में अणु 4p (क/२)^{२ =} pक^२ [4p (d/2)²=p d²] आयतन में घूमता है। अत: म (U) वेग से चलने में व अणु p क^२म (p d²U) आयतन घेर लेगा। आवोगाद्रो की संख्या सं (N) हो तो इस आयतन में p क^२म सं (p d²UN) अणुओं के केंद्र प्रति सेकंड होंगे, अर्थात् प्रत्येक सेकंड में अणुओं के p क^२म सं (p d²UN) संघात होंगे और मध्यमान अवधि पथ

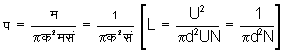
होगा। इससे ज्ञात होता है कि मध्यमान मुक्त अणु के घनत्व का प्रतिलोमसमानुपाती (inversely proportional) होता है तथा दाब घनत्व का अनुक्रमानुपाती है। इसलिए मध्यमान पथ दाब का प्रतिलोमसमानुपाती है।

अणु के सापेक्ष वेग के कारण मध्यमान पथ का संशोधन - हमने कल्पना की थी कि केवल एक अणु चलता है और बाकी सब अणु स्थिर हैं, परंतु वस्तुत: सब अणु इतस्तत: उसी मध्यमान वेग म (U) से चलते रहते हैं। यह आवश्यक है कि हम दो अणुओं का मध्यमान सापेक्ष वेग निर्धारित करें। दो अणुओं के चलने की दिशाओं में मान लें कोण ण (q ) हैं। दोनों अणुओं के वेग का वेक्टर दिष्ट अंतर (vector difference), जिसको सापेक्ष वेग कहते हैं

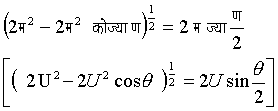
होता है। अणुओं की ण (q ) दिशा में चलने की संभाविता 2p ज्या ण.ताण/4p [2p sinq .dq /4p]होती है। इसलिए अणुओं का सापेक्ष वेग होगा

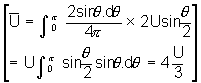
इस कारण संघातों की संख्या के अनुपात से बढ़ती है और मध्यमान मुक्तपथ के अनुपात में कम हो जाता हैं।

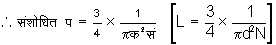
प्रयोग द्वारा अणुओं के मध्यमान मुक्त पथ का निर्धारण - गैस की सांद्रता अथवा श्यानता, विसरण तथा ऊष्मावाहकता के गुणांकों में प (L) राशि होती है। इस कारण प्रयोग द्वारा इन गुणांकों का निर्धारण करके प (L) का मूल्य ज्ञात हो सकता है। इन सब विधियों से प्राप्त किए हुए प (L) के मूल्य समान होते हैं। अणु का व्यास क (d) तथा आवोगाद्रो संख्या सं (N) ज्ञात करके

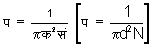
व्यंजक द्वारा भी प (L) का मूल्य ज्ञात होता हैं। सन् १९२१ में मैक्सबॉर्न (Max Born) ने पहले पहल एक सुंदर प्रयोग करके प (L) का मूल्य ज्ञात किया। प्रयोग की विधि इस प्रकार है। काच की प्लेट पर निम्न दाब के आवरण में चाँदी के अणुओं का स्तर उत्पन्न किया जाता है। अणु के उद्गमस्थान से प्लेट के अंतर पर स्तर की मोटाई घातांक नियमानुसार निर्भर होती है। स्तर की मोटाई का नियम मो = मो_०ई- ^य/प [D=D₀e- ^x/l] समीकरण से दर्शित किया जाता है। यहाँ मो (D), य (x) और प (L) क्रमानुसार मोटाई, अंतर और मध्यपानपथ के दर्शक अक्षर हैं। य_१ (x₁) और य_२ (x₂) अंतर पर स्तर की मोटाई पूर्वोक्त नियमानुसार क्रम से मो_१= मो_०ई- ^य_१^/प [D₁=D₀e- ^x₁^/L] तथा

मो_{२ =} मो_०ई- ^य_२^/प [D₂=D₀e- ^x₂^/L] होती है।

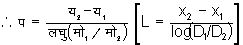
स्तर की मोटाई ज्योतिर्मापी (photometer) से ज्ञात की जाती है। गैस की दाब ५.८� १०- ^३ मिलीमीटर रखकर चाँदी के अणुओं का प (L) = 1.7 सेंटिमीटर प्राप्त हुआ और दाब ४.५� १०- ^३ मिलीमीटर रखने से प का मूल्य २.४ सेंटिमीटर आया। अन्य रीतियों से ज्ञात किए हुए मूलय ऊपर दिए हुए मूल्यों के समान ही थे।

श्यानता ओर मध्यमान मुक्त पथ - श्यानता और मध्यमान मुक्त पथ का संबंध दिखानेवाला व्यंजक हम ज्ञात कर सकते हैं। हम मान लेंगे कि दो संघातों के बीच के समयांतर में अणु स (L) अंतर पार करता है। अ और प और ब ये तीन पृष्ठतल हैं। अ और ब से प का अंतर स है (देखें चित्र २)। प पृष्ठतल में होनेवाले संवेग के विनिमय का हम विचार करेंगे। विनिमय में व अणु होंगे जो अ पृष्ठ से टकराकर प पृष्ठतल में आ रहे हैं और वे अणु जो ब

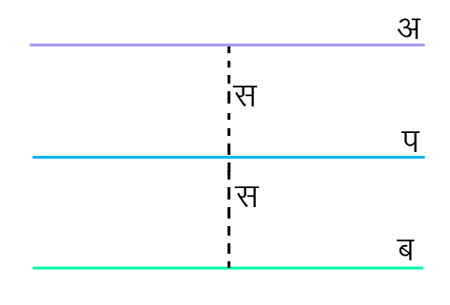
चित्र २.

पृष्ठतल से प पृष्ठतल में जाते हैं। अ पृष्ठ से प की ओर आनेवाले अणुओं का संवेग उतना ही होगा जितना ब से प की ओर जानेवाले अणुओं का है। मान लें, प पृष्ठतल में गैस के अणुओं का वेग उ (u) है तथा अ और ब के बीच के २स (2L) अंतर में वेग की प्रवणता (gradient) है। इस कारण अ पृष्ठ में अणु का संवेग होगा। यदि एक घन सेंटीमीटर में सं (N) अणु हैं, और अणु का मध्यमान वेग वे (v) है तो मैक्सवेल के वेगावतरण नियम के अनुसार अ पृष्ठतल से प पृष्ठ की ओर संवे (Nv) अणु प्रयाण करेंगे। इन अणुओं का संपूर्ण संवेग

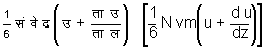
है और ब से प पृष्ठतल में आनेवाले अणुओं के संवेग

का योग

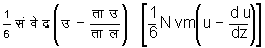
है। संवेग की वास्तविक वृद्धि इन दो राशियों के अंतर के बराबर होती है। इस कारण वास्तविक वृद्धि

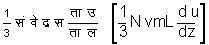
हुई। यह वृद्धि चलनेवाली गैस के स्तर के बल के बराबर होती है। श्यनता की व्याख्या से स्तर पर स्पर्शीय बल है, अत:

�

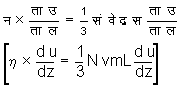
अथवा न= घ वे स (h =r vL)। इसी प्रकार हम मध्यमान और ऊष्मा की संवाहकता के गुणांक का संबंध स्थापित कर सकते हैं। यह संबंध निम्नलिखित समीकरण द्वारा व्यक्त किया जाता है :

के = सं द्र वे वि स = घ वे वि स

[K=NmvC_vL=r vC_vL],

यहाँ के (K) ऊष्मा संवाहकता और वि (C_v) स्थिर आयतन के लिए गैस की विशिष्ट ऊष्मा है।

ब्राउनीय गति (Brownian motion) - द्रव्य का अणु सिद्धांत जिस प्रमेय पर निर्भर है उसके अनुसार द्रव्य के अणु बड़ी तीव्रता से इतस्तत: चलते हैं। हमने ऊपर देखा है कि अणु सिद्धांत के परिणामों का सत्यापन करने में साधारणत: सफलता प्राप्त हुई है, परंतु अणु की गति का प्रत्यक्ष प्रमाण बहुत काल पर्यंत प्राप्त नहीं हुआ। सन् १८२७ में ब्राऊन नाम के वनस्पति वैज्ञानिक ने पहले पहल यह देखा कि यदि द्रव्य का कोलाइडी (colloidal) विलयन अति सूक्ष्मदर्शी द्वारा देखा जाए तो उसमें अणुओं की इतस्तत: हलचल होती हुई दिखाई देती है। इससे यह ज्ञात हुआ कि द्रव्य के अणु जो विलायक में विलयित होते हैं, वे इस कारण इतस्तत: घूमते हैं कि उनको विलायक के अणु इधर उधर धक्के देते हैं। ब्राऊन ने प्रयोग से निम्नलिखित अनुमान निकाले : (१) अणुओं की गति द्रव की भँवर धारा तथा संनयन धारा के कारण नहीं होती, (२) जिस बरतन में विलयन है उस बरतन को हिलाने से अणु की गति में परिवर्तन नहीं होता, (३) जिन द्रवों का श्यानता गुणांक कम होता है उनमें गति अधिक होती है, (४) विलायक में द्रवित कणों का आकार कम होने से कणों की गति बढ़ती है तथा (५) यह हलचल निरंतर रहती है और मंद नहीं होती।

इस गति को ब्राऊनीय गति कहते हैं। विलायक के अणुओं में ऊष्माजन्य गति निरंतर होती है, और ब्राउनीय गति के लिए आवश्यक शक्ति इन अणुओं की ऊष्माजन्य गति से मिलती है। विलयन में लटके हुए कण चारों ओर से विलायक के अणुओं से टकराते हैं। संभाविता के नियमानुसार धक्का देनेवाले अणुओं की संख्या सब दिशाओं में समान न होने के कारण कणों पर कुटिल असंतुलित बल पड़ता है और इस बल के प्रभाव से कण इधर उधर हिलने लगते हैं। सन् १९०८ में रस वैज्ञानिक पैरे (Perrin) ने ब्राउनीय गति के विषय को व्यवस्थित आधार पर रखा। आइन्स्टाइन (Einstein) तथा स्मॉलुचॉस्की (Smoluchowski) ने ब्राउनीय गति में चलनेवाले कणों का आयाम ज्ञात करने के लिए गणित सूत्र प्रस्थापित किए। अतिसूक्ष्मदर्शी की सहायता से कणों का आयाम निर्धारित किया जा सकता है और इस निर्धारण से आइन्स्टाइन के गणितसूत्रों की सत्यता प्रस्थापित हो गई। गैसों के अणुओं की गति जिन जिन कारकों पर निर्भर होती है, उन्हीं कारकों पर द्रव में लटके हुए अणुओं की गति भी निर्भर होती है। पृथ्वीतल से गैस की ऊँचाई और उस ऊँचाई पर एक घन सेंटिमीटर में स्थित अणुओं की संख्या का संबंध लाप्लास (Laplace) ने सूत्र रूप में दिया। यह सूत्र न = न_०ई- ^{द्र सं त्व ऊ/थटा} [h =h ₀e- ^{m N g h/RT}] है। यहाँ न_० (h ₀) किसी स्थान पर प्रति घन सेंटिमीटर में अणुओं की संख्या है और न (h ) उस स्थान से ऊ (h) ऊँचाई पर स्थित अणुओं की संख्या है, सं (N) आवोगाद्रो संख्या और द्र (m) अणु की मात्रा है। पेरैं ने गेंद का ऐलकोहाल में विलयन बनाकर पानी में डाला और इस प्रकार गोंद के कोलाइडी कण बनाए। इन कणों का सूक्ष्म निरीक्षण करके पेरैं ने लाप्लास के सिद्धांत की सत्यमा प्रस्थापित की। आइन्स्टाइन ने ब्राउनीय गति के कारण होनेवाले कण के विस्थापन के लिए एक व्यंजक ज्ञात किया, जो इस प्रकार है:

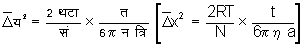
यहाँ य^२ ( x²) मध्यमान विस्थापन का वर्ग है, जो य (x) अक्ष की दिशा में होता है तथा त्रि (a) कण की त्रिज्या है। इस व्यंजक की सत्यता पेरैं ने स्थापित की।

ब्राउनीय गति और मिलिकैन के तैलविंदु पर प्रयोग - मिलिकैन (Millikan) ने फुहारे द्वारा हवा में तेल के बिंदु उत्पन्न करने की योजना सफलता से पूरी की। पृथ्वी के गुरुत्वाकर्षण के कारण नीचे गिरनेवाले इन बिंदुओं का मिलिकैन विद्युद्बल द्वारा हवा में संतुलित रखता था। इन प्रयोगों से मिलिकैन ने इलेक्ट्रॉन का विद्युदावेश ज्ञात किया और तेल के विंदुओं की ब्राउनीय गति भी ज्ञात की। आवोगाद्रो संख्या और इलेक्ट्रॉन इ (e) का गुणनफल २.८८ � १०^१४, मिलिकैन ने विद्युत्स्थैतिक एकांक में प्राप्त किया। विद्युद्विश्लेषण के प्रयोगों से यह गुणनफल २.८९� १०^१४ ज्ञात हुआ।(धुडिराज भास्कर देवधर)