द्रवबल विज्ञान (हाइड्रॉमिकेनिक्स Hydromechanics) गणित की वह शाखा है, जिसमें (स्थिर अथवा प्रवहयुक्त) द्रवों के व्यवहार का अध्ययन होता है। यदि द्रव गतिहीन है तो इस अध्ययन को द्रवस्थितिविज्ञान (Hydrostatics) कहते हैं और यदि द्रव गतियुक्त है तो उसे द्रवगतिविर्ज्ञान (Hydrodynamics) कहते हैं। दोनों उपशाखाओं में मान लिया जाता है कि द्रव सतत पदार्थ है और विसरण तथा पृष्ठतनाव उपेक्षणीय हैं। द्रवगतिविज्ञान में समान्यतया द्रव का घनत्व अचर मान लिया जाता है, किंतु जब विपुल द्रवपुंज की अथवा अत्यत द्रुतगामी द्रव की बात हो तो घनत्व की यह मान्यता अनौपचारिक हो जाती है। पहले द्रवबल विज्ञान के अंतर्गत गैस-पुंज की भी संतुलनावस्था अथवा उसकी गति का अध्ययन होता था, किंतु अब यह वायुगतिविज्ञान नाम से अलग विषय की बन गया है। द्रवगतिविज्ञान और वायुगतिविज्ञान को मिलाकर तरलगतिविज्ञान भी कहते हैं।
द्रवस्थितिविज्ञान - जब डोरे से बँधे बटखरे आदि किसी भारी पिंड को पानी में डुबोकर डोरे को पकड़े रहते हैं, तब देखा जाता है कि इतना बल नहीं लगाना पड़ता, जितना बल उस पिंड को पानी से बाहर खींच लेने पर लगता है। ऐसा क्यों होता है इसका कारण सबसे पहले गणितज्ञ आर्किमीडीज़ (१८७-२१२ ई.पू.) ने ज्ञात किया और इस सिद्धांत का प्रतिपादन किया कि किसी द्रव में डूबे हुए पिंड पर द्रव एक ऊर्ध्वाधर उत्क्षेपी बल लगाता है, जो पिंड द्वारा विस्थापित द्रव के भार के बराबर होता है। उत्क्षेप का निदान करते समय तरल दाब की संकल्पना सामने आती है, अर्थात् एक ऐसे बल की जो तरल अपने से संपर्क में आए हुए पिंड के प्रत्येक पृष्ठ अल्पांश पर लगाता है। ऐसी दाब के अस्तित्व का आभास हमें यही देखकर मिल जाता है कि छिद्र से बाहर निकलते हुए पानी को रोकने के लिए बल की आवश्यकता होती है। आर्किमीडीज़ के नियम की व्याख्या इस परिकल्पना के आधार पर दी जा सकती है कि तरल दाब तरल के संपर्कवाले पिंड के पृष्ठ-अल्पांश पर लंबत: क्रिया करता है।
तरल दाब - दाब की संकल्पना में स्पष्टता लाने के लिए दाबप्रचंडता की परिभाषा यह कह कर की गई है कि यह तरल द्वारा लगाए हुए बल और तल के क्षेत्रफल के अनुपात की सीमा है, जब क्षेत्रफल शून्य की ओर अग्रसर होता है। प्रचंडता की सकंल्पना का एक महत्वपूर्ण लाभ यह है कि तरल के प्रत्येक बिंदु पर इसका मान ज्ञात किया जा सकता है। नीचे सिद्ध किया गया है कि तरल के किसी बिंदु पर सभी दिशाओं में दाबप्रचंडता का मान बराबर रहता है और इसे उस बिंदु पर द्रवस्थैतिक दाव कहते हैं। संकेताक्षर द (P) द्वारा इसे प्रकट करते हैं। इस दाब का आयाम ''बल प्रति एकक क्षेत्रफल'' है। सामान्यतया

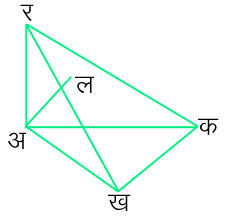
चित्र १.
एक लघु चतुष्फलकीय द्रवंश अ क र ख पर विचार करें, जिसमें अ पर मिलनेवाले तीन फलक परस्पर लंब हैं। मान लें कि फलक अ क र पर दाब (प्रचंडता), जो दिशा अ ख में हैं, दख है। फलक अ र ख पर दिशा अ क में दक, फलक अ क ख पर दिशा अ र में दर और फलक क र ख पर इसके लंबत: दिशा अ ल में दख है, तो उस सीमावस्था में, जब चतुष्फलक की कोरें शून्य हो जाती हैं, बिंदु अ पर दाब तीन लंब दिशाओं में दक, दख दग और दिशा अ ल में दख है। यदि � ल अ र = को है तो यही कोण क र ख और क अ ख फलकों के बीच है, इसलिए
D क र ख कोज्या को = D अ क ख
लंब फलकों के क्षेत्रफल दो कोरों के गुणनफल और चतुष्फलक का आयतन तीन कोरों के गुणनफल के अनुपात में है। इसलिए कोरों के लघु होने के कारण चतुष्फलक का भार (आयतन � घनत्व) फलकों पर दाबबल (दाब � क्षेत्रफल) की तुलना में उपेक्षणीय है। इस प्रकार चतुष्फलक केवल चार दाबों के कारण ही संतुलित है। अत: प्रत्येक दिशा में परिणामी बल शून्य है, उदाहरणत: दिशा अ र में चारों दाबों के संघटक लेने पर,
D क अ ख. दर = D क र ख. दल कोज्या को, अर्थात् दर = दख। यह भी सिद्ध किया जा सकता है कि यदि द्रव का घनत्व अचर है, तो दाब गहराई का समानुपाती है और क्षैतिज तल में समान रहता है। इस सिद्धांत के अनुसार ही - 'खोजहि ददक सदा निज स्तर'। जलप्रबंध में इस गुण का उपयोग किया जाता है और उत्स्त्रुत कूप भी इसी कारण चल पाते हैं। इसके आधार पर लेओनार्डो दि वींचि (१४५२-१५१९ ई.) ने तरल दाब की संचरणशीलता का यह नियम प्रतिपादित किया कि यदि बिना ज्यामितीय परिसीमाएँ बदले द्रव के किस बिंदु पर दाब में कोई वृद्धि कर दी जाए तो उतनी ही वृद्धि द्रव के प्रत्येक विंदु पर स्वत: हो जाती है। बल का परिमाण दाब और क्षेत्रफल के गुणनफल के बराबर होने के कारण छोटे क्षेत्रफल पर थोड़ा बल लगाने का परिणाम वही होता है, जो बड़े क्षेत्रफलके पिस्टन पर बड़े बल के लगाने का। जलचालित दावक, ब्रेक आदि इसी नियम पर आधारित हैं। इसी कारण बाँध (देखें बाँध) शीर्ष की अपेक्षा आधार पर अधिक चौड़े बनाए जाते हैं, तथा जल में अत्यधिक गहराई पर काम करनेवालों को दाब की प्रतिरक्षा के लिए इस्पात के कवच पहनने पड़ते हैं।
द्रव का मुक्त तल (धारक के संपर्क से दूर) और अमिश्र्य तरलों के बीच का तल, दोनों क्षैतिज होते हैं। यदि दो द्रवों के बीच का तल वक्र है, उसकी वक्रता-त्रिज्याएँ त्र१, त्र२ (R1 R2) हैं तथा त (T) पृष्ठतनाव है और तलवक्रता की ओर दाब द१ (P1) तथा दूसरी ओर द२ (P2) है तो
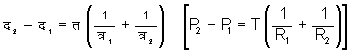
क्षैतिज तल के लिए दाहिना पक्ष शून्य हो जाता है (देखें पृष्ठतनाव)।
प्लवित पिंड का संतुलन और स्थायित्व - जब कोई पिंड कई एक द्रवों में अंशत: डूबा हो, तो उसके भार का संतुलन पिंड द्वारा विस्थापित विभिन्न द्रवराशियों के भारत के बराबर उत्क्षेपों से होता है और प्रत्येक उत्क्षेप को उस राशि के गुरुत्वकेंद्र पर, जिसे उत्प्लावकता केंद्र कहते हैं, ऊर्ध्वाधर दिशा में लगा माना जा सकता है।
यदि किसी प्लवित पिंड को ऐसी विभिन्न स्थितियाँ दी जाँए, जिन में उसके द्वारा विस्थापित द्रवों का भार के बराबर रहे, तो उत्प्लावक केंद्र का बिंदुपथ उत्प्लावक तल कहलाता है और संतुलनावस्था में पिंड की वह स्थिति होती है जिसमें उत्प्लावक केंद्र और पिंड के गुरुत्वकेंद्र के बीच की दूरी महत्तम या न्यूनतम होती है। महत्तम दूरी होने पर संतुलन अस्थायी और न्यूनतम होने पर स्थायी होता है। उत्प्लावकतल के मुख्य वक्रताकेंद्रों को आप्लव केंद्र (metacentre) कहते हैं। यदि उपप्लव केंद्र में पिंड के गुरुत्व केंद्र ग से ऊपर है तो म के संगत मुख्य विस्थापनों के लिए संतुलन स्थायी है, यदि नीचे है, तो अस्थायी और यदि ग तथा म एक ही बिंदु हैं, तो संतुलन उदासीन है। ग म उत्प्लावन तल पर अभिलंब होती है। इस प्रकार ग से उत्प्लावन तल पर अभिलंब खींचकर संतुलन स्थितियों को ज्ञात किया जा सकता है।
द्रवगतिविज्ञान - गतियुक्त द्रव की गति के अध्ययन की दो प्रमुख विधियाँ हैं। एक विधि में द्रव के प्रत्येक कण गति निम्नांकित समीकरणों द्वारा ज्ञात की जाती है :
य = फ१ (स), र = फ२ (स), ल = फ३ (स)
[x=f1 (t), y=f2 (t), z=f3 (t)]
यहाँ य, र, ल, (x, y, z) किन्हीं निर्दिष्ट निर्देशाक्षों के सापेक्ष कण के समय स (t) पर निर्देशांक हैं। स को चर मानकर कण पथ और अवकलन द्वारा कण का वेग ज्ञात किया जा सकता है, किंतु यह विधि अत्यंत जटिल है। दूसरी विधि में निर्दिष्ट क्षण स (t) पर गति रेखाएँ और अचर वेगतलों द्वारा वेग वंटन जाना जाता है। गति रेखा वह वक्र है, जिसके प्रत्येक बिंदु पर स्पर्शी तत्क्षण उस विंदु पर स्थित कण के वेग की दिशा में है। इस प्रकार वेग की दिशा गति रेखा की स्पर्शी से और माप अचर वेगतल द्वारा प्राप्त हो जाती है।
गति को तब सदा सम (अपरिवर्ती) कहते हैं, जब प्रत्येक बिंदु पर द्रव का वेग, दिशा और परिमाण में समय के सापेक्ष अचर रहता है, अर्थात् वेग व (q) के संघटक व१, व२, व३ (u, v, w), स (t) से स्वतंत्र हैं। ऐसी गति में कणपथ और गतिरेखा एक ही होती हैं और उन्हें धारारेखा (streamline) कहते हैं। अत्यणु (infinitesimal) तल की परिरेखा से होकर खींची गई धारारेखाओं
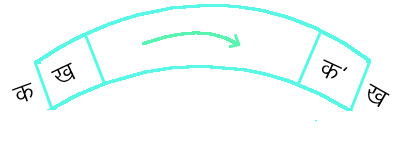
चित्र २.
से धारानलिका (stream tube) बनती है। इसके भीतर का द्रव सदा इसके भीतर ही रहता है और द्रव्यमान तथा ऊर्जा के अविनाशिता के नियमों का उपयोग कर महत्वपूर्ण अनुमितियाँ प्राप्त की जा सकती हैं।
सातत्य समीकरण - मान लें किसी धारानलिका का क्षेत्रफल क (A) और ख (B) की दो समीपस्थ अनुप्रस्थ काटें हैं और इन काटों के बीच का द्रव कुछ समय बाद क'(A' ) तथा ख'(B') काटों के बीच पहुँच जाता है। फिर, मान लें कि क पर द्रववेग व (q) तथा कफ़ पर व'(q') है, जो जितना द्रव क से समय तास (dt) में निकलता है उतना ही क'से भी निकलता है, इसलिए
कघव तास = क'घ'व'तास (Ar qdt=ar'q'dt)
जहाँ घ (r ) घ'(r') क तथा क� पर द्रवें के घनत्व हैं। इस प्रकार
क घ व = क� घ� व� (A r q=A� r � q� )
यह सदासम
गतिवाले द्रव
के लिए सातत्य समीकरण
है। इसका अधिक
व्यापक रूप जा गति
के सदासम न होने
पर भी लागू
है, ल्योनार्ड आयलर
ने सन् १७५५ में दिया।
निर्देशाक्षों के
समांतर कोरों
तायों, तार, ताल
(dx, dy, dx) के
एक लघु घनाभ के
भीतरवाले द्रव
के द्रव्यमान में
परिवर्तन की
दर ![]() ताय
तार ताल [
ताय
तार ताल [![]() ]
है। इसकी समता
घनाभ के फलकों
से होकर प्रवहित
द्रव्यमान की परिवर्तन
दरों के योग
से करने पर
अंत में निम्नलिखित
सातत्य समीकरण
मिलता है :
]
है। इसकी समता
घनाभ के फलकों
से होकर प्रवहित
द्रव्यमान की परिवर्तन
दरों के योग
से करने पर
अंत में निम्नलिखित
सातत्य समीकरण
मिलता है :
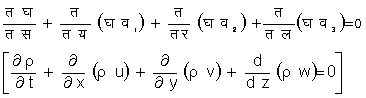
यदि द्रव असंपीड्य है तो
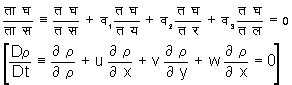
और सातत्य समीकरण का निम्नलिखित सरल रूप हो जाता है :
![]()
गति, ऊर्जा और दाब के समीकरण - दालाँवेयर (D' Alambert) के सिद्धांत का प्रयोग कर आयलर ने तीन गतिसमीकरण निम्नलिखित रूप के दिए :
![]()
जहाँ, ब१, ब२, ब३, (x, y, z) संपूर्ण बाह्य बल (प्रति एकक द्रव्यमान) के, जिनमें गुरुत्वाकर्षण भी संमिलित हैं, संघटक हैं।
बेर्न्ली
समीकरण - मान
लें कि चित्र २. में
धारानलिका
के खंड क ख का आयतन
अ (V), घनत्व
घ (r ),
वेग व (q),
(गुरुत्वाकर्षण
जैसे) बाह्य बलों
की स्थितिज ऊर्जा
ऊ(W ) है और
खंड क� ख�
(A� B�
) के लिए
संगत राशियों
को प्रासचिन्ह
लगाकर प्रकट
करते हैं, तो
प्रथम खंड के लिए
गतिज ऊर्जा ![]() घ
अ ब२ (
घ
अ ब२ (![]() r
Vq2) दाब
ऊर्जा द अ (p V)
और स्थितिज ऊर्जा
घ अ ऊ(r V
W ) है। अब क्योंकि
अ = अ�
(V=V� ),
ऊर्जा अविनाशिता
के निमय से, ऊष्मा
का स्थानांतरण
न होने की दशा
में,
r
Vq2) दाब
ऊर्जा द अ (p V)
और स्थितिज ऊर्जा
घ अ ऊ(r V
W ) है। अब क्योंकि
अ = अ�
(V=V� ),
ऊर्जा अविनाशिता
के निमय से, ऊष्मा
का स्थानांतरण
न होने की दशा
में,
द�
/घ� +
![]() व�
२+
ऊ� =
द/घ+
व�
२+
ऊ� =
द/घ+![]() व२+
ऊ।
व२+
ऊ।
[P�
/r � +![]() q�
2+W �
=P/r +
q�
2+W �
=P/r +![]() q2+W
]
q2+W
]
यही समीकरण सर्वप्रथम डेनियल वेनूली (सन् १७००.८२) ने दिया था और इसके अनेक उपयोग हैं। यदि द्रवधारा में किसी रोक से दूर बिंदु के लिए राशियाँ द, ब, ऊ(p, q, W ) हैं और रोक पर द� , व� (= ०), ऊ� (p� , q� =o� , W ) तो द� (p� ) के लिए समीकरण यह है :
द�
/घ + ऊ�
= द/घ + ![]() व२
+
ऊ [P�
/r +W =p/r
+q2+W ]
व२
+
ऊ [P�
/r +W =p/r
+q2+W ]
और यदि ऊ (W ) अचर है तो
द�
= द + ![]() घ
व२ [p�
=p+
घ
व२ [p�
=p+![]() r
q2]
r
q2]
अर्थात्
दाब रोक पर
![]() घ व२
(
घ व२
(![]() r
q2) अधिक है।
r
q2) अधिक है।
टॉरिसेली नियम - किसी जलंकुंड के द्वारक से विसर्जित पानी के वेग व (q) और जलतल से द्वारक की गहराई च (h) में सनिकट संबंध ब२= २ ग च (q2=2gh) होता है, जहाँ ग (g) गुरुत्वाकर्षणजनित त्वरण है। उपर्युक्त नियम को टॉरिसेली ने १६४३ ई. में सुझाया। ऐसा करने में इन्होंने गैलिलियो के निर्वाध गिरते पिंडों के प्रयोगों के परिणामों पर आधारित युक्तियों का आश्रय लिया। पूर्वोक्त वेर्नूली के प्रथम समीकरण से यह तुरंत प्राप्त हो जाता है, क्योंकि घ� = घ (r � = r ), जलतल पर वेग व� (V� ) शून्य है; ऊ� -ऊ= ग च (W � - W = gh) और द्वारक तथा मुक्त पृष्ठ पर दाब संनिकटत: बराबर होने से द� = द (p� =p)
द्विआयामी गति - ऐसी द्रवगति को, जिसमें धारारेखाएँ एक स्थिर समतल के समांतर हैं और इस समांतर समतलों के संगत बिंदुओं पर वेग माप तथा दिशा में एक समान है, द्विआयामी गति कहते हैं। इन समतलों में से एक को य अ र (x o y) मान सकते हैं, जिससे व३= ० (w=o)। तब असंपीड्य द्रव के लिए सातत्य समीकरण का निम्नलिखित सरल रूप हो जाता है :
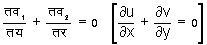
यदि गति अघूर्णनशील है, तो एकमान फलन फ (f ) ऐसा होता है कि
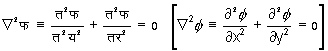
तब, जैसा कि संमिश्र चर सिद्धांत से ज्ञात है, ऐसा फलन ध (y ) भी होता है जो फ (f ) के समान लाप्लास समीकरण को संतुष्ट करता है, और फ+ i ध (f + iy), य + i र (x + iy) का नियमित फलन है। इसे धारा फलन कहते हैं और
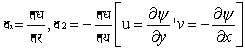
इन व्यंजकों से स्पष्ट है कि आवर्तता शून्य है। कई स्थितियों में द्विआयामी गति, वास्तविक गति का अच्छा सन्निकटन होता है और संमिश्र चर सिद्धति के अनुकोण निरूपण उपविषय का इसके अध्ययन में अत्यंत महत्वपूर्ण उपयोग है।
अक्षसममित गति - ऐसी गति को अक्षसममित गति कहते हैं, जिसमें एक निश्चित ऋजु रेखा (जिसे अक्ष कहते हैं) से जानेवाले सभी समतलों में एक सी गति है। ऐसी गति का उदाहरण है अन्यथा विश्रामावस्था के द्रव में परिक्रमण ठोस का परिक्रमणाक्ष की दिशा में चलना। ऐसी गति में और द्विआयामी गति में कुछ बातों में सादृश्य है, उदाहणत: धाराफलन का अस्तित्व, जो स्टोक्स के नाम से प्रसिद्ध है।
चक्रमान - किसी (सीमित) रेखा के अनुदिश लिया गया रेखासमाकल
![]() (व१ताय
+
व२तार +
व३ताल)(
(व१ताय
+
व२तार +
व३ताल)(![]() u
dx+v dy+ w dz) वक्र के अनुदिश
वाहमान कहलाता
है। यदि वक्र बंद
है तो समाकल
को वक्र के परित:
चक्रमान हते हैं।
यदि फ (य, र, ल)
[ f (x, y, z)]
कोई एकमान फलन
है और
u
dx+v dy+ w dz) वक्र के अनुदिश
वाहमान कहलाता
है। यदि वक्र बंद
है तो समाकल
को वक्र के परित:
चक्रमान हते हैं।
यदि फ (य, र, ल)
[ f (x, y, z)]
कोई एकमान फलन
है और
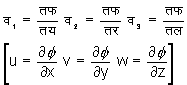
तो समाकल अर्थात् चक्रमान शून्य है और गति अघूर्णनशील कहलाती है। फलन फ (f ) को वेगविभव कहते हैं। यदि द्रव असंपीड्य है, तो लाप्लास समीकरण
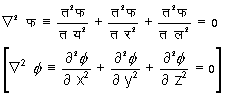
किसी रोक के पार्श्व से प्रवह इस समीकरण के ऐसे हल से मिल जाता है, जिसमें रोक के सापेक्ष, द्रव के वेग का रोक की अभिलंब दिशा में संघटक शून्य है। जब गति सदा सम होती है, तब रोक पृष्ठ पर दाब बेर्नूली के नियम से मिल जाता है और यह निष्कर्ष निकलता है कि रोक पर द्रव द्वारा लगाए बलों का परिणामी या तो शून्य है या केवल बलयुग्म, जो अनुभव के प्रतिकूल है और दालाँबेयर की पहेली के नाम से प्रसिद्ध है।
भ्रमिल गति - यदि चक्रमान शून्य न हो तो उस दशा में राशियाँ
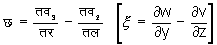
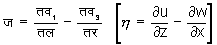
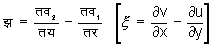
को भ्रमिलता के संघटक कहते हैं। समीकरण
ताय/छ = तार/ज = ताल/झ [dx/x =dy/h =dz/x ]
से प्राप्त वक्रों को अवर्त रेखाएँ कहते हैं और एक लघु बंद वक्र के बिंदुओं से जानेवाली भ्रमिल रेखाओं से भ्रमिल नलिका बनती है। ऐसी नलिका में समाए हुए द्रव को भ्रमिल झिल्लिका कहते हैं। इस विषय पर हेल्महोल्ट्ज़ (१८२१-९४ ई.) और लॉर्ड केल्विन (१८२४-१९०७ ई.) की गवेषणाओं में से एक यह है कि यदि बाह्य बलों का विभव एकमान है तो ऐसे द्रवों में जिनमें दाब केवल घनत्व पर निर्भर है चक्रमान की न उत्पत्ति हो सकती है और न विनाश।
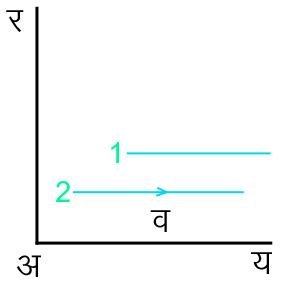
चित्र ३.
श्यान प्रवाह - गतियुक्त द्रव में स्पर्शी बलों के अध्ययन का सूत्रपात न्यूटन ने उस समस्या पर विचार कर किया जब द्रव एक ही दिशा में, मान लें अय में, (देखें चित्र ३.) बहता है और वेग व (u) में परिणति लंब दिशा अर में है। स्तर १. स्तर २. की अपेक्षा अधिक द्रुत है और वेगों के अंतर के अनुसार उसपर एक कर्षण श्यान बल लगाता है। न्यूटन की परिकल्पना थी कि स्तर १. और २. को अलग करनेवाले लघु क्षेत्रफल क्ष (A) पर कर्षण बल
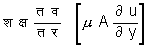
है, जहाँ श (m ) को द्रव का श्यानता गुणांक कहते हैं। इसका आयाम संवेगभाजित क्षेत्रफल का है। ह = श/घ (n = m / r ) को गतिज श्यानता कहते हैं।
गतिज सिद्धांत में श्यानकर्षण का कारण यह है कि स्तर १. के कुछ द्रुतगामी अणु स्तर २. में और स्तर २. के कुछ मंदगामी अणु स्तर १. में आ जाते हैं। विक्षुब्ध गति में इसी प्रकार एक स्तर से दूसरे में संवेग का स्थानांतरण होता है और अणुओं के स्थान में आवर्तमय कण समुदायों का आदान प्रदान होता है।
यह सिद्ध किया जा सकता है कि यदि त्रिज्या त्र (a) और लंबाई ल (१) की ऋजुनलिका के सिरों पर दाबों का अंतर द (p) है तथा श्यानता गुणांक श (m ) है तो प्रति एकक कालांतर में नलिका में होकर आयतन
p त्र४ द/८ शल [p a4p/8m l]
का द्रव बहेगा। इस नियम का सत्यापन केशिकानलिकाओं वाले प्रवाह के लिए अथवा चौड़ी नलिकाओं में अत्यंत मंदगति के लिए हो जाता है। इस नियम की प्रयोज्यता रेनाल्ड संख्या र = वत्र/ह
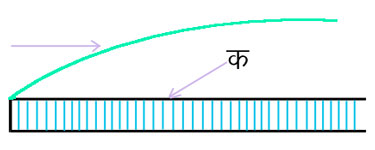
चित्र ४.
(R=ua/n ) पर निर्भर है; यदि यह क्रांतिक मान से बढ़ जाती है तो गति श्यान नहीं रहती। तेल जैसे अति श्यान द्रव के लिए यह नियम साधारणतया लागू है।
परिसीमा स्तर - द्रव की वास्तविक गति कदाचित् ही अघूर्णनशील होती हो, या श्यान प्रवाह के नियमों का पालन करती हो। इसलिए प्रांटिल (Prandtle) ने इस सिद्धांत का प्रतिपादन किया है कि निमज्जित पिंड अथवा धारक पात्र की दीवार से सटे हुए क्षीण परिसीमास्तर में प्रवाह संनिकटत: श्यान है और इस स्तर के बाहर अघूर्णनशील। प्रवह की दिशा के समांतर समतल दीवार से सटे प्रवाह में (चित्र ४.) परिसीमा स्तर की मोटाई अग्रकोर दूरी के अनुसार बढ़ती है। यदि श्यानता कम है, तो यह मोटाई आरंभ में अत्यंत न्यून होती है।
द्रव में निमज्जित पिंड के पृष्ठ की परिसीमा स्तर में प्रवाह तब नियमित होता है जब प्रवाह की दिशा में दाब घटता हो। इसके विपरीत अवस्था में धारारेखाएँ परिसीमा से अलग हो जाती हैं और लगभग उस स्थान से जहाँ वे अलग होती हैं उनके संगम के स्थान तक विमुक्ति आवर्त झिल्लियाँ अथवा भँवर पिंड के पीछे बन जाते हैं।
सं.ग्रं.- ए.एस. रैमज़े : हाइड्रोस्टैटिक्स (१९४६), कँब्रिज; जी.एस. स्टार्लिग : मिकैनिकल प्रॉपर्टीज़ ऑव मैटर (१९५१), सेंट मार्टिस; फ्रैंक टाइलर : मिकैनिक्स ऐंड हाइड्रोस्टैटिक्स (१९५४), सेंट मार्टिस; हाइड्रोडाइनैमिक्स (१९५६), मैकमिलन।
(हरिश्चंद्र गुप्त)�