दोलन ऐसी गति का नाम है जिसमें कोई वस्तु या द्रव्यकरण किसी परिमित पथ पर चलकर पुन: पुन: अपने पूर्व स्थान पर लौट आता है और उसके विस्थापन, वेग तथा त्वरण किसी नियत काल के पश्चात् पुन: पुन: अपने पूर्वमानों को प्राप्त कर लेते हैं। झूले की तथा घड़ी के लोलक की गति इसी प्रकार की होती है। इसे आवर्त गति भी कहते हैं। जब यह दोलन बहुत जल्दी जल्दी होता है तब वह कंपन कहलाता है।
दोलन का पथ सरल रेखात्मक भी हो सकता है, जैसे सर्पिल कमानी से लटके हुए गोले के ऊपर नीचे की दिशा में होनेवाले दोलनों का

चित्र १.
पथ। यह वृत्ताकार भी हो सकता है, जैसे लोलक का पथ। यह अंतहीन बंद वक्र के रूप में भी हो सकता है, जैसे जब कोई द्रव्यकण एक केंद्र बिंदु के चारों ओर किसी वृत्त पर, अथवा किसी भी अन्य आकृति के बंद वक्र पर बार बार चक्कर लगाता है।
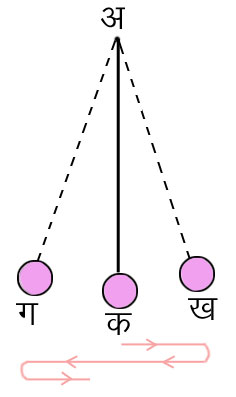
चित्र १. में लोलक अ क का गोला विराम अवस्था में क पर स्थित है। अब यदि कुछ बल लगाकर हम उसे ख तक विस्थापित करके छोड़ दें तो गुरुत्वाकर्षण के कारण गोले पर एक प्रतिविस्थापन बल लगेगा, जिसकी दिशा विस्थापन की दिशा से विपरीत होगी। यह गोले को खींचकर क की ओर लौटा लाने का प्रयत्न करेगा। फलत: गोला ख से क की ओर चलने लगेगा और उसका वेग निरंतर बढ़ता ही जाएगा, क्योंकि जब तक वह क पर नहीं पहुँच जाएगा तब तक कुछ न कुछ बल उसपर गति की दिशा में लगता ही रहेगा। इस वेग के कारण वह क पर रुकेगा नहीं, आगे ही बढ़ता जाएगा। अब उसपर गति से विपरीत दिशा में बल लगेगा। इससे वेग क्रमश: घटने लगेगा और ग पर पहुँचकर वह ठहर जाएगा जहाँ क गउ क ख। इसके बाद पहले ही की तरह वह क की ओर लौटेगा और फिर ख तक जा पहुँचेगा। यदि वायु आदि का प्रतिरोध उसके वेग को न घटाए तो गोला बार बार इसी प्रकार इधर से उधर दौडता ही रहेगा। क से ख और वहाँ से ग तक जाकर पुन: क पर लौट आने को एक पूर्ण दोलन कहते हैं। इसके बाद दूसरा दोलन प्रारंभ होता है, जिसमें पहले दोलन की प्रत्येक बात का पुनरावर्तन होता है। जितना समय प्रथम दोलन में लगा था ठीक उतना ही दूसरे, तीसरे तथा बाद के प्रत्येक दोलन में लगेगा। इस समय को आवर्तकाल कहते हैं। इसके अपरिवर्तित रहने के कारण ही घड़ी में लोलक की उपयोगिता है।
यदि आवर्तकाल T सेकंड हो तो एक सेकंड में होनेवाले दोलनों की संख्या n=1/T होगी। यह उस दोलन की आवृत्ति कहलाती है। दोलनकारी गोले का महत्तम विस्थापन क ख = क ग उसका आयाम कहलाता है।
जो बातें लोलक के दोलनों के सबंध में ऊपर लिखी गई हैं, वे सब प्रत्येक प्रकार के दोलन में पाई जाती हैं। किंतु प्रतिविस्थापन बल सदा गुरुत्व के कारण नहीं होता, यह बहुधा प्रत्यास्थता (देखें प्रत्यास्थता) के कारण भी होता है। तब दोलन प्रत्यास्थ दोलन कहलाता है।
सरल आवर्त दोलन - जिस दोलन या कंपन में विस्थापन द्र का समय द्य के साथ होनेवाला परिवर्तन समीकरण y=a sin w t .... (१) के द्वारा व्यक्त किया जा सके उसे सरल आवर्त दोलन कहते हैं। इसमें a तथा w अचर संख्याएँ हैं। स्पष्टत: a ही y का महत्तम मान है। अत: यही दोलन का आयाम है और समय द्य में 2p /w की वृद्धि होने पर y अपने पूर्व मान को प्राप्त कर लेता है, क्योंकि
a sin w 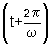 =a
sin w t
=a
sin w t
अत: आवर्तकाल (T=2p /w ) है और आवृत्ति (n=w /2p ) है।
इसलिए यह गतिसमीकरण निम्नलिखित रूपों में भी लिखा जा सकता है :
(क)
y=a sin![]() t,
(ख) y=a sin 2 p
n t
t,
(ख) y=a sin 2 p
n t
समीकरण (१) से प्रकट होता है कि किसी क्षण (द्य) पर दोलनकारी वस्तु का वेग
v=�=![]() =a
w cos w t..... (2)
=a
w cos w t..... (2)
तथा
त्वरण f=�=![]() =-
a w 2 sin w
t=- w 2y..... (3)
=-
a w 2 sin w
t=- w 2y..... (3)
और यदि उसका द्रव्यमान m हो तो
प्रतिविस्थापन बल=m f=m�=- m w 2 y..... (4)
अत: सरल आवर्त दोलन में यह बल विस्थापन का समानुपाती होता है और ऋण चिन्ह प्रकट करता है कि इसकी दिशा विस्थापन से विपरीत होती है।
यह भी स्पष्ट है कि यदि यह बल प्रत्यास्थता के कारण हो तो इस समानुपात की अचर संख्या ्ध्र का मान दोलायमान वस्तु के प्रत्यास्थता गुणांक तथा उसकी लंबाई चौड़ाई पर निर्भर होगा। अत: आवर्तकाल भी इन्हीं पर अवलंबित होगा।
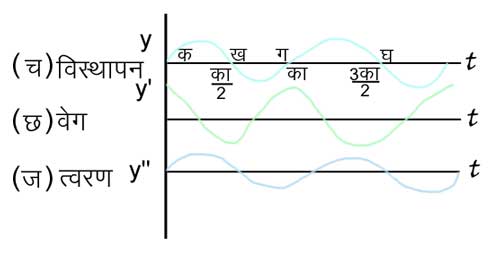
विस्थापन वक्र - चित्र २. (च) में सरल आवर्त दोलन के विस्थापन का लेखाचित्र दिखाया गया है। क ख ग घ समय द्य का अक्ष है और इसपर लंबवत् विस्थापन y का अक्ष है। यह लेखाचित्र ज्यावक्र कहलाता है। इसमें आयाम a है तथा क ग = का (T) आवर्तकाल है। इसी प्रकार चित्र २ (छ) तथा २ (ज) में दोलनकारी वस्तु के वेग
चित्र २.
तथा त्वरण दिखाए गए हैं। इनसे स्पष्ट हो जाता है कि जिस समय विस्थापन महत्तम होता है, उस समय त्वरण भी महत्तम होता है किंतु वेगउ ० होता है और जब विस्थापन y= 0 होता है तब त्वरण भी ० होता है, किंतु वेग महत्तम हो जाता है।
ऊर्जा - यदि वायु आदि की रगड़ अथवा अन्य किसी कारण से ऊर्जा दोलनकारी वस्तु को दी गई थी वह उसमें ज्यों की त्यों बनी रहती है। कभी वह पूर्णत: स्थितिज रूप में रहती है, यथा चित्र १ में ख तथा ग पर, और कभी वह पूर्णत: गतिज रूप में रहती है, यथा विरामविंदु क पर। अन्यत्र उसका कुछ भाग स्थितिज रूप में तथा कुछ भाग गतिज रूप में रहता है, अर्थात् दोलन की ऊर्जा स्थितिज से गतिज रूप में और इसके बाद गतिज से स्थितिज रूप में बार बार बदलती रहती है। यह भी स्पष्ट है कि गतिज ऊर्जा का मान होगा Ek=m v2=m a2 w 2 cos2 w t* अत: इसका महत्तम मान होगा m a2 w 2* यही पूर्ण ऊर्जा का मान है और यह आयाम के वर्ग का समानुपाती है।
दोलन की कला - समीकरण (१) में जिस कोण की ज्या (sine) ली गई है, वह अर्थात् w t,दोलन का कलाकोण कहलाता है। जिस प्रकार चंद्रमा की कला से यह ज्ञात होता है कि उसका कितना अंश प्रकाशित है उसी तरह दोलन की कल भी यह प्रकट करती है कि दोलन का कितना अंश व्यतीत हो चुका है और उसकी तात्क्षणिक अवस्था क्या है। आयाम a तथा आवर्तकाल T का मान कुछ भी क्यों न हो, किंतु जब कलाकोण w t=0, 2p , 4p आदि हो तो विस्थापन महत्तम =+a होता है, जब w t=p , 3p , 5p आदि हो तो विस्थापन महत्तम =- a होता है और जब w t=p /2, 3p /2, 5p /2 आदि हो तो विस्थापनउ ० होता है।
दो दोलनों के तात्क्षणिक कलाकोणों के अंतर को कलांतर कहते हैं। ऐसे दोलनों के गति समीकरणयों लिखे जाते हैं : y=a sin w t, Ÿ=b sin (w t+d ) और d इन दोलनों का कालांतर है। जब यह कलांतर ०� अथवा 2p रेडियन = ३६०� हो तो उनकी कलाएँ समान कहलाती हैं। ऐसे दोलनों के महत्तम विस्थापन साथ साथ और एक ही दिशा में होते हैं, अथवा दोनों अपने विरामबिंदुओं पर एक साथ तथा एक ही दिशा में पहुँचते हैं। जब कलांतर रेडियनउ १८०रू का होता है, तब कलाएँ विपरीत होती हैं। तब दोनों दोलनों में विस्थापन महत्तम तो एक ही क्षण पर होते हैं, किंतु विपरीत दिशाओं में और जिस समय एक का महत्तम वेग एक दिशा में होता है उसी समय दूसरे का विपरीत दिशा में होता है।
कलांतर को व्यक्त करने की एक युक्ति और भी है। कलाकोण w t=2p t/T होने के कारण इसे आवर्तकाल के अंश t/T के द्वारा भी व्यक्त किया जाता हैं। इस दृष्टि से समान कला को 0, T, 2T आदि का कलांतर कहा जाता है और विपरीत कला को T/2, 3 T/2, 5T/2 आदि का कलांतर कहा जाता है।
यदि दो दोलनों के आवर्तकाल बराबर हों, तब तो उनका कलांतर जितना प्रारंभ में होता है उतना ही बराबर बना रहता है। किंतु यदि आवर्तकाल बराबर न हों तो कलांतर क्रमश: बदलता जाता है।
दोलन का रूप - आवृत्ति तथा आयाम में कोई अंतर न होने पर भी सरल आवर्त दोलनों से भिन्न भी कई प्रकार के दोलन हो
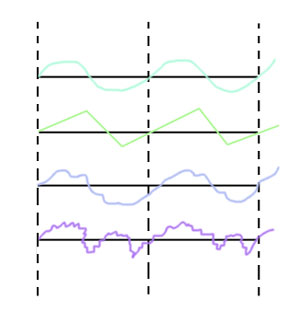
चित्र ३.
सकते हैं। इस भेद को समझने का सबसे अच्छा साधन है विस्थापनवक्र। चित्र ३. में कई विस्थापन वक्र दिखाए गए हैं। इन सबमें आवृत्ति तथा आयाम बराबर हैं, किंतु विस्थापन, वेग आदि के परिवर्तन के क्रम भिन्न भिन्न हैं। इन सबकी गति समीकरण द्वारा व्यक्त नहीं हो सकती और न वेग ऊर्जा आदि ही उस समीकरण से प्राप्त हो सकते हैं। इनके गति समीकरण अत्यंत जटिल होते हैं। इनका भेद विस्थापन-वक्र की आकृति के द्वारा ही आसानी से समझा जा सकता है। अत: इस आकृति को ही दोलन का रूप कहते हैं। आवृत्ति तथा आयाम ही की तरह रूप भी प्रत्येक दोलन का अत्यंत महत्वपूर्ण लक्षण है।
सरल आवर्त दोलनों का संयोजन - यह संभव है कि एक ही द्रव्यकरण में दो प्रकार के दोलन एक साथ हो रहे हों। ऐसी दशा में उस कण का विस्थापन दोनों दोलनों द्वारा उत्पन्न विस्थापनों का संमिलित परिणाम होता है। तब निम्नलिखित घटनाएँ होती हैं :
(क) यदि दोनों संघटक विस्थापन संरेख हों तब तो परिणामी विस्थापन, प्रत्येक क्षण पर दोनों विस्थापनों का बीजीय योग होता है - अर्थात् यदि दोनों एक दिशा में हों तो जोड़ के बराबर और विपरीत दिशाओं में हों तो अंतर के बराबर। दोनों दोलनों के विस्थापन-वक्र खींचकर प्रत्येक क्षण का परिणामी विस्थापन अंकित करने से परिणामी विस्थापन-वक्र प्राप्त हो जाता है। यदि दोनों संघटक दोलनों की आवृत्तियाँ बराबर हों तब तो परिणामी गति भी सरल आवर्त ही होती है। यदि वे संमेय हों, अर्थात् दोनों आवृत्तियों का अनुपात कोई पूर्णांक हो, तब भी परिणामी गति भी सरल आवर्त ही होती है। यदि व संमेय हों, अर्थात् दोनों आवृत्तियों का अनुपात कोई पूर्णांक हो, तब भी परिणामी गति आवर्तगति तो होती है, किंतु सरल नहीं। उसका रूप भिन्न प्रकार का होता है।
इस प्रकार दो से अधिक संघटक दोलनों के संयोजन से विभिन्न रूपों के दोलन प्राप्त हो सकते हैं। वस्तुत: फूरियर ने गणित द्वारा प्रमाणित कर दिया है कि प्रत्येक असरल दोलन अनेक सरल आवर्त दोलनों का ही संयोजित परिणाम होता है। यदि असरल दोलन का आवर्तकाल T हो तो इन संघटक दोलनों के आवर्तकाल T, T/2, T/3, T/4 आदि होते हैं। यदि इन संघटक दोलनों के आयाम तथा कलाएँ यथोचित निर्धारित कर दी जाएँ तो परिणामी विस्थापन वक्र बिलकुल वैसा ही प्राप्त हो जाता है जेसा उस असरल दोलन का था। फूरियर के नाम से प्रख्यात प्रमेय के द्वारा इन संघटक दोलनों के आयामों का पता आसानी से लगाया जा सकता है। इस दृष्टि से दोलनों के रूपभेद का कारण उनके संघटक सरल आवर्त दोलन और उनके आयाम ही हैं।
यदि संघटक दोलनों की आवृत्तियाँ असंमेय हों तो परिणामी गति आवर्तगति नहीं होती और उसे दोलन की संज्ञा नहीं दी जा सकती।
(ख) यदि संघटक दोलन समकोणिक हों तो उनके विस्थापनों का संयोजन सदिश राशियों के संयोजन के समचतुर्भुज नियम के अनुसार होता है और तब दोलनपथ सरलरेखात्मक न रहकर वक्ररूप धारण कर लेता है। चित्र ४. में ऐसे कुछ वक्रपथ दिखाए गए हैं। जब आवृत्तियाँ बराबर हों, द१=द२, तब तो पथ वृत्ताकार अथवा दीर्घ वृत्ताकार हो जाता है (चित्र ४. में १ और २)। जब द१=२द२ हो तो पथ की आकृतियाँ चित्र ४. के ३ और ४ के समान हो जाती हैं। द१/द२ का मान इससे अधिक होने पर दोलनपथ और भी जटिल आकृति के हो जाते हैं।
(ग) जब दो संरेख संघटक दोलनों की आवृत्तियों में बहुत थोड़ा अंतर हो तब दोलन विलक्षण प्रकार का हो जाता है, जिसे विष्कंपन कहते हैं। यदि आवृत्तियाँ द१ तथा द२ हो और आयाम a तथा b हों तो
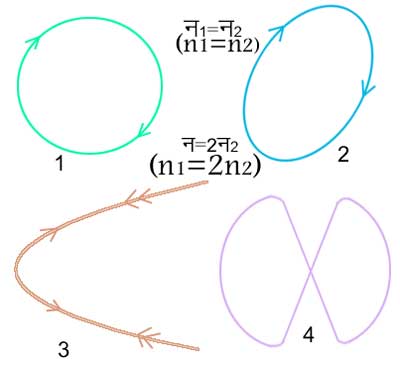
चित्र ४.
परिणामी दोलन का आयाम कभी तो a+b के बराबर होकर महत्तम हो जाता है और कभी a- b के बराबर होकर न्यूनतम हो जाता है और यह घट बढ़ निश्चित आवर्तकाल के अंतर से एक सेकंड में n1- n2 बार होती है।
आवमंदित दोलन - सरल-आवर्त दोलन में आयाम अचर होता है और ऊर्जा का क्षय बिलकुल नहीं होता, किंतु यह केवल आदर्श मात्र है। वास्तविक दोलनों में वायु के घर्षणात्मक प्रतिरोध आदि अनेक कारणों से ऊर्जा की हानि होती रहती है और आयाम क्रमश: घटता जाता है और अंत में दोलनों का अंत हो जाता है। ऐसे दोलन को अवमंदित दोलन कहते हैं। जब प्रतिरोध वेग का समानुपाती होता है तब इसका गतिसमीकरण समीकरण (३) में एक और पद - 2k� जोड़कर प्राप्त किया जाता है :
�=- 2k�- w 2y..... (5)
इसका हल है y=ae- kt sin (qt+e )...... (६)
जहाँ आवर्तकाल T=2p /q है और q2=w 2- k2 है।
यह आवृत्ति n=q/2p इस दोलन की स्वाभाविक अथवा प्रकृत आवृत्ति कहलाती है और अवमंदन के अभाव में जो आवृत्ति n0=w /2p होती वह मुक्त आवृत्ति कहलाती है। इसमें ध्यान देने योग्य सबसे महत्वपूर्ण बात यह है कि इसका आयाम ae- kt अचर नहीं है। उसका मान उत्तरोत्तर नियमपूर्वक घटता जाता है। नियम यह है कि यदि किसी क्षण t पर महत्तम विस्थापन a1 हो तथा इसके पश्चात् T/2, 2T/2, 3T/2, आदि कालांतरालों के बाद होनेवाले महत्तम विस्थापन a2, a3, a4 आदि हों तो
![]()
इसी तरह
![]()
इस गुणांक e- kT/2 को अपक्षय कहते हैं। k अवमंदन गुणांक कहलाता है। यह भी स्मरण रहना चाहिए कि इस दोलन की स्वाभाविक आवृत्ति द युक्त आवृत्ति द० के बराबर नहीं है। किंतु बहुधा त्त् का मान इतना कम होता है कि इन आवृत्तियों का अंतर उपेक्षणीय समझा जा सकता है।
प्रणोदित दोलन - उपर्युक्त दोलनों में बाह्य बल प्रारंभ में ही केवल क्षण भर के लिए लगाया जाता है। इसके बाद दोलनकारी वस्तु में बाह्य ऊर्जा का प्रवेश नहीं होता। किंतु बहुधा दोलन ऐसे भी होते हैं जिनमें बाह्य बल बराबर इस प्रकार लगता रहता है, जिससे जितनी ऊर्जा का क्षय अवमंदनकारी प्रतिरोध के कारण होता रहता है, उतनी ही ऊर्जा की प्राप्ति भी उसे बराबर होती रहती है। परिणाम यह होता है कि प्रतिरोध की उपस्थिति में भी आयाम घटता नहीं। ऐसे दोलन को प्रणोदित दालन कहते हैं और ऐसे बल को प्रणोदक बल। यह बल कई प्रकार का हो सकता है। घड़ी के लोलक में यह रुक रुककर प्रति T/2 सैकंड के अंतराल से लगता है। सारंगी के तार पर गज द्वारा तथा बाँसुरी की वायु पर फूँक द्वारा यह अन्य प्रकार से, परंतु बराबर, लगता रहता है। किंतु सबसे सरल प्रकार का प्रणोदक बल वह होता है जिसका परिणाम सरल आवर्त रूप से बदलता रहता है, अर्थात् जिसे निम्नलिखित समीकरण के द्वारा व्यक्त किया जा सकता है :
F=Fosin pt.
ऐसे बल की उपस्थिति में दोलन का समीकरण होगा
�=- 2k�- w 2y+Fo sin pt....... (७)
इसका पूरा हल है y=ae- kt sin (qt+e )+A sin (pt-d )...... (८)
जहाँ
A=![]() ,
q2=w 2- k2
तथा tan d
=
,
q2=w 2- k2
तथा tan d
=![]() । स्पष्टत:
इसमें दो दोलन
सम्मिलित हैं। प्रथम
तो प्रणोदक बल
के अभाव में होनेवाला
अवमंदित दोलन
है, जो थोड़ी
ही देर में क्षीण
होकर नष्ट हो
जाता है। अत: इसका
महत्व अधिक नहीं
है। दूसरा दोलन,
जो बराबर
चलता रहता है,
वह है
। स्पष्टत:
इसमें दो दोलन
सम्मिलित हैं। प्रथम
तो प्रणोदक बल
के अभाव में होनेवाला
अवमंदित दोलन
है, जो थोड़ी
ही देर में क्षीण
होकर नष्ट हो
जाता है। अत: इसका
महत्व अधिक नहीं
है। दूसरा दोलन,
जो बराबर
चलता रहता है,
वह है
y=A sin (pt- d )
यही प्रणोदित दोलन है। इसकी आवृत्ति p/2p न तो मुक्त आवृत्ति w /2p के बराबर होती है और न स्वाभाविक आवृत्ति q/2p के बराबर। यह स्पष्टत: प्रणोदक बल की आवृत्ति के बराबर होती है।
इसका आयाम है
स्पष्ट है कि यह महत्तम तब होगा जब p=w हो, अर्थात् जब प्रणोदक बल की आवृत्ति दोलित वस्तु की मुक्त आवृत्ति के बराबर हो। प्रणोदित दोलन की इस महत्तम ऊर्जा वाली अवस्था का नाम है अनुनाद।
अन्य प्रकार के दोलन - किसी वस्तु या द्रव्यकण आवर्तगति के अतिरिक्त किसी भी द्रव्यहीन भौतिक राशि के परिमाण में यदि अवर्त का परिवर्तन हो रहा हो तो उसे भी दोलन या कंपन ही कहते हैं, यथा ताप का दोलन, चुंबकीय बल का दोलन, वैद्युत बल का दोलन। ये भी निम्नलिखित रूप के समीकरणों द्वारा व्यक्त किए जाते हैं, यथा T=T0 sin 2p nt; H=H0 sin 2p nt; E0=E0 sin 2p nt. इनके भी अवमंदित तथा प्रणोदित दोलन तथा अनुवाद होते हैं और इन दोलनों के संयोजन के भी वेही नियम हैं जो द्रव्यकण के दोलनों के लिए ऊपर बताए जा चुके हैं।
(निहालकरण सेठी)