दिक् और काल का संबध हमारे नित्य व्यवहार में इतना अधिक आता है कि इनके विषय में कुछ अधूरी सी किंतु दृढ़ धारणाएँ हमारे मन में बचपन से ही होना स्वाभाविक है। कवियों ने दिक् और काल की गंभीर, विशाल तथा सुंदर कल्पनाओं का वर्णन किया है। दर्शन में और पाश्चात्य मनोविज्ञान में भी इनके विषय में पुरातन काल से सोच विचार होता आ रहा है। कणाद (३०० ई. पू.) के वैशेषिक दर्शन में आकाश, दिक् और काल की धारणाएँ सुस्पष्ट दी गई हैं और इनके गुणों का भी वर्णन किया गया है। इंद्रियजन्य अनुभवों से जो ज्ञान मिलता है उसमें दिक् और काल का संबंध अवश्य ही होता है। इस ज्ञान की यदि वास्तविकता समझा जाए तो दिक् और काल वस्तविकता से अलग नहीं हो सकते। प्रत्येक दार्शनिक संप्रदाय ने वस्तविकता, दिक् और काल, इनके परस्पर संबंधों की अपनी अपनी धारणाएँ दी हैं, जिनमें ऐकमत्य नहीं है। गणित में भी दिक् और काल का अप्रत्यक्ष रीति से संबंध आता है। अत: प्रतिष्ठित भौतिकी का विकास इन्हीं धारणाओं पर निर्भर रहा। भौतिकी के कुछ प्रायोगिक फल जब इन धारणाओं से विसंगत दिखाई देने लगे, तब ये धारणाएँ विचलित होने लगीं एवं आपेक्षितावाद (देखें आपेक्षितावाद) ने दिक् और काल का नया स्वरूप स्थापित किया, जो अनेक प्रयोगों द्वारा प्रमाणित और फलत: अब सर्वसम्मत हो चुका है। दिक् तथा काल का यह नया स्वरूप केवल भिन्न ही नहीं वरन् (हमारी इनके विषय की व्यावहारिक कल्पनाओं के कारण) समझने में भी अत्यंत कठिन है, क्योंकि इसके प्रतिपादन में विशिष्ट गणित का उपयोग आवश्यक होता है। अत: जहाँ जहाँ दिक् तथा काल संबंध आता है उसका स्पष्टीकरण पहले स्थूल दृष्टि से, तत्पश्चात् सूक्ष्म दृष्टि से और अंत में भौतिकी की दृष्टि से करना अधिक सरल होगा।
इंद्रियजन्य अनुभवों से जो दिक् के गुणों का प्रत्यय आता है, उससे दिक् के विभिन्न प्रकार माने जा सकते हैं। अनुभवों के बुद्धि पर जो परिणाम होते हैं उनका पृथक्करण करके धारणाएँ बनती हैं। इस प्रकार स्वानुभव से दिक् की जो धारणा बनती है उसे 'स्व-दिक्' अथवा 'व्यक्तिगत दिक्' कहा जाता है। इंद्रियजन्य अनुभवों में अनेक अनुभव समस्त व्यक्तियों के लिए समान होते हैं, और ऐसे अनुभव जिस घटना से मिलते हैं, उसे 'वास्तव' कहा जाता है। वास्तव घटनाओं के समुदायों से 'वास्तविकता' की धारणा बनती है।
इंद्रियों से दृष्टि, स्पर्श, ध्वनि, रस और गंध के अनुभव मिलते हैं, किंतु ये अनुभव सर्वदा विश्वास के योग्य होते हैं, ऐसा नहीं है। प्रकाशकीय संभ्रम तो सुप्रसिद्ध हैं ही। स्पर्श के भी संभ्रम व्यवहार में नित्य प्रतीत होते हैं, जैसे दो दाँतों के बीच की खोह जीभ को जितनी लगती है उससे कम छोटी उँगली को लगती है। प्राय: ऐसा ही प्रकार सब तरह के इंद्रियजन्य अनुभवों का होता है। अत: इन अपूर्ण अनुभवों से व्यक्तिगत दिक् की जो धारणा बनती है वह भ्रममूलक ही होती है। मापनदंड तथा अन्य उचित यंत्रों की सहायता से इंद्रियों की मर्यादित ग्राहकता बढ़ाई जा सकती है और इस प्रकार अनेक घटनाओं का भ्रमनिरसन हो सकता है। प्रयोगों में मापन करके दिक् की जो धारणा होती है उसे ''भौतिक दिक्'' कहा जाता है। मापन के लिए मापनदंड का उपयोग किया जाता है।
अनुभवों में दिक् का संबंध चार प्रकार से आता है और इन चारों प्रकारों पर विचार करके दिक् के गुणों की व्यावहारिक कल्पनाएँ बनती हैं। किसी वस्तु के स्थल का निर्देश जब वहाँ कहकर किया जाता है, तब दिक् के एक स्वरूप की कल्पना आती है और इसका अर्थ यह भी माना जाता है कि दिक् का अस्तित्व (अनुभवों से) स्वतंत्र है। किसी वस्तु के स्थल का निर्देश अन्य वस्तु के 'सापेक्ष' करने पर दिक् की 'सापेक्ष स्थिति' में दूसरा स्वरूप दिखई देता है। दिक् का तीसरा स्वरूप वस्तुओं के 'आकार' से मिलता है, जिससे दिक् की विभाज्यता की भी कल्पना की जा सकती है। आकाश की ओर देखने से दिक् की 'विशालता' (अथवा अनंतता) का चौथा स्वरूप दिखाई देता है। इन चार प्रकार के स्वरूपों से ही प्राय: दिक् के संबध में व्यावहारिक धारणाएँ बनती हैं और दिक् के गुण भी सूचित होते हैं।
घटनाओं से प्राप्त इंद्रियजन्य अनुभवों का विचर किया जाए तो उनके दो प्रकार होते हैं। घटनाओं के स्थानभेद से दिक् की कल्पना होती है और उनके क्रम-भेद से काल की कल्पना होती है। इस प्रकार दिक् और काल हमारी विचारधारा में संदिग्ध रूप से प्रवेश करते हैं। दिक् जैसा ही काल भी व्यक्तिगत (अथवा स्व-काल) होता है और प्रत्येक व्यक्ति की कालगणना स्वतंत्र तथा स्वेच्छ होती है। इतना ही नहीं, इस स्व-काल की गणना में भी परिवर्तन होता है और वह व्यक्ति के स्वास्थ्य, अवस्था इत्यादि स्थितियों पर निर्भर करता है, जैसे, किसी कार्य में मनुष्य मग्न हो तो काल तेजी से कटता है। अत: व्यक्तिगत अथवा स्व-काल विश्वास योग्य नहीं रहता। किसी प्राकृतिक घटना से - दिन और रात से - जो काल का मापन होगा वह व्यक्तिगत नहीं रहेगा और सब लोगों के लिए समान होगा। अत: ऐसे काल को सार्वजनिक काल कहा जाता है। दिन और रात काल के स्थूल विभाग हैं। इनके छोटे विभाग किए जाएँ तो व्यवहार में कालमापन के लिए वे अधिक उपयुक्त होते हैं। इसलिए प्रहर, घटिका, पल विपल अथवा घंटा, मिनट, सेकंड इत्यादि विभाग किए गए। सामान्यत: काल का मापन घड़ी से होता है।
दिक् की भाँति काल के भी चार स्वरूप व्यवहार में दिखाई देते हैं। किसी घटना अथवा अनुभव से 'कब?' प्रश्न उपस्थित होता है और इसका दिक् विषयक 'कहाँ' से साम्य है। इस कल्पना से काल का अस्तित्व (अनुभवों से) स्वतंत्र समझा जाता है। किसी घटना के काल के सापेक्ष दूसरी घटना का वर्णन करते समय काल का सापेक्ष स्वरूप दिखाई देता है। दो घटनाओं के बीच के काल से काल का जो स्वरूप दिखाई देता है वह दिक् के आकार से समान है। वैसे ही काल के अनादि, अनंत इत्यादि विशेषणों से काल की विशालता दिखाई दती है। दिक् तथा काल के चारों स्वरूपों को, या गुणों को कहिए, मिलाकर विचार करने पर इनके विषय में हमारी जो धारणाएँ बनती हैं उनको 'स्व' या 'व्यक्तिगत' अथवा 'मनोवैज्ञानिक' दिक् और काल कहा जाता है।
दिक् तथा काल की धारणाओं को निश्चित रूप देने के लिए उनका मापन करने के साधन आवश्यक होते हैं। दिक् के मापन के लिए दृढ़ पदार्थों के दंड, औजार तथा यंत्र उपयोग में लाए जाते हैं। इन उपकरणों से लंबाई, कोण, क्षेत्रफल, आयतन इत्यादि वस्तुओं के गुणों के मापन होते है। इन मापनों के समय बिंदु, रेखा, समतल इत्यादि की धारणाएँ बनती जाती हैं। जब अनेक पुनरावृत्तियों से ये धारणाएँ दृढ़ हो जाती हैं, तब बिंदु, रेखा, समतल इत्यादि का स्थान मौलिक होता है और भौतिक वस्तुएँ इन धारणाओं से दूर हो जाती हैं। अब इन धारणाओं की और यूक्लिडीय ज्यामिति की मौलिक धारणाओं की समानता स्पष्ट होगी। दृढ़ वस्तुओं को समाविष्ट करके दिक् के, अथवा वस्तुओं के, मापन से दिक् की जो धारणा होती है उसे ज्यामितीय अथवा यूक्लिडीय दिक् कहा जाता है। यह स्पष्ट है कि दिक् की इस धारणा से उसके जो गुण समझे जाते हैं वे केवल यूक्लिडीय ज्यामिति की परिभाषाओं, स्वयंसिद्ध और कल्पनाओं के ऊपर ही निर्भर होते हैं। दिक् की हमारी व्यावहारिक धारणा और मापन से निश्चित की हुई यह ज्यामितीय धारणा, क्रमश: हमारी स्थूल दृष्टि और सूक्ष्म दृष्टि के स्वरूप हैं।
यूक्लिडीय ज्यामिति पर निर्धारित दिक् की यह धारणा यद्यपि स्वाभाविक दिखाई देती होगी, तथापि इसका विश्लेषण करने की आवश्यता है। यूक्लिडीय ज्यामिति में कुछ परिभाषाएँ (जैसे बिंदु, रेखा, तल इत्यादि) तथा कुछ स्वयंसिद्ध तथ्य दिए हुए हैं और इनका तार्किक दृष्टि से विकास किया गया है। ये धारणाएँ केवल काल्पनिक और स्वतंत्र हैं। थोड़ा ही विचार करने पर यह स्पष्ट होगा कि यूक्लिडीय ज्यामिति का व्यवहार की वस्तुओं से कोई भी वास्तविक संबंध नहीं है। अपनी मूल कल्पनाओं को विकसित करते समय उनका परस्पर तर्कसंगत संबंध रखना और एक 'काल्पनिक' गणित शास्त्र का निर्मांण करना, इतना ही इस ज्यामिति का मूल उद्देश्य था। इस उद्देश्य में यह ज्यामिति अत्यंत ही सफल रही। इस ज्यामिति का और भी विस्तार करके उसे 'व्यावहारिक' बनाने के लिए 'आदर्श दृढ़ वस्तु' की परिभाषा यह है कि इसके दो बिंदुओं का अंतर किसी भी परिस्थिति में उतना ही रहता है। मापन दंड अथवा अन्य औजारों का उपयोग इसी विशेषता पर निर्भर करता है। वस्तुत: इस प्रकार 'आदर्श दृढ़ वस्तु' को समाविष्ट करने पर यूक्लिडीय ज्यामिति का स्वरूप बदल जाता है और उसको अब हम भौतिकी का एक विभाग समझ सकते हैं। किंतु व्यवहार में यूक्लिडीय ज्यामिति का यह परिवर्तन इस दृष्टि से नहीं देखा जाता। मापन करने पर व्यावहारिक वस्तुओं के मापन के लिए यूक्लिडीय ज्यामिति के सिद्धांत यथार्थ दिखाई देते हैं। इसलिए यूक्लिडीय ज्यामिति को 'वास्तविक' समझा जाने लगा।
व्यावहारिक अनुभव और यूक्लिडीय ज्यामिति का दृष्टि से न्यूटन ने अपनी दिक् और काल की धारणाएँ निश्चित रूप से प्रस्तुत की और प्रतिष्ठित भौतिकी का विकास प्राय: वर्तमान शताब्दी के प्रारंभ तक इन्हीं धारणाओं पर निर्भर रहा। न्यूटन ने दिक् को स्वतंत्र सत्ता समझकर उसके गुण भी दिए। न्यूटन के अनुसार दिक् के गुण सर्व दिशाओं में तथा सर्व बिंदुओं पर समान ही होते हैं, अर्थात् दिक् समदिक्, समांग तथा एक समान है। अत: पदार्थों के गुण दिक् में सभी स्थानों पर समान ही होते हैं। दिक् अनंत है और न्यूटन के दिक् में लंबाई, काल तथा गति से अबाधित रहती है। काल के विषय में भी न्यूटन ने अपनी धारणा दी है और यह धारणा भी उस समय के भौतिकी के विकास के अनुसार ही थी। न्यूटन के अनुसार काल भी एक स्वतंत्र सत्ता है। काल का विशेष गुण यह है कि वह समान गति से सतत और सर्वत्र 'बहता' है और किसी भी परिस्थिति का उसके ऊपर कोई भी परिणाम नहीं होता। काल भी अनंत है। सारांश में, न्यूटन के अनुसार दिक् तथा काल दोनों ही स्वतंत्र और निरपेक्ष सत्ताएँ होती हैं। न्यूटन आदि की यांत्रिकी इन्हीं धारणाओं पर निर्भर थी। यांत्रिकी में गति और त्वरण, इन दोनों के लिए दिक् और काल को निश्चित रूप देना आवश्यक था और उस समय तो इन धारणाओं में कोई भी त्रुटि दिखाई नहीं देती थी। वैसे ही भौतिकी में न्यूटन का इतना प्रभाव था कि इन धारणाओं पर शंका प्रदर्शित करना संभव नहीं था।
बोल्याई, लोबातचेवस्की, रीमान इत्यादि गणितज्ञों ने यह सिद्ध किया कि यूक्लिडीय ज्यामिति के कुछ स्वयंतथ्यों में उचित परिवर्तन करने पर अयूक्लिडीय ज्यामितियों का निर्माण हो सकता है। यद्यपि अयूक्लिडीय ज्यामितियों के अनेक सिद्धांत यूक्लिडीय ज्यामिति के सिद्धांतों से भिन्न होते हैं, तथापि वे अयोग्य नहीं होते हैं। विशेषत: रीमान के अयूक्लिडीय ज्यामिति से यह स्पष्ट हुआ कि यूक्लिडीय ज्यामिति ही केवल मौलिक नहीं है। यद्यपि अयूक्लिडीय ज्यामितियाँ कल्पना करने में कठिन होती हैं, तथापि तर्कसम्मत होने से उनके फल अत्यंत रोचक तथा उपयुक्त होते हैं। इनमें तीन से अधिक विमितियों के दिक् की (जिसे हम 'अति दिक्' कह सकते हैं) जो कल्पना होती है, उस दिक् की वक्रता की कल्पना विशेष रूप से उपयुक्त हुई।
न्यूटन के दिक् में किसी बिंदु का स्थान तीन कार्तिसीय निर्देशांकों य१, य२, य३ (x1, x2, x3) से निश्चित होता है। इस यूक्लिडीय दिक् में तीन ही विमितियाँ होती है, अत: तीन कार्तिसीय निर्देशांक पर्याप्त होते हैं। यदि पास के दो बिंदु अ (य१, य२, य३) (A{x1, x2, x3}) और ब(य१+ तय१,य२+ तय२,य३+ तय३) [B (x1+d x1, x2+d x2, x3+d x3)] लिए जाएँ (यहाँ त य = य में स्वल्प वृद्धि और त = d अर्थात् डेल्टा), तो इन दो बिंदुओं का अंतर तश (d s) निम्नलिखित समीकरण द्वारा मिलता है:
तश२= तय१२+ तय२२+ तय३२ (d s2=d x12+d x22+d x32) ..... (1)
इस व्युत्पत्ति में य माना गया है कि जिस आदर्श दृढ़ दंड से यह अंतर मापित होता है उसकी लंबाई में किसी भी परिस्थिति में परिवर्तन नहीं होगा।
यदि दो विभक्तियों के समतल पर ऊपर निर्दिष्ट दो बिंदु लिए जाएँ, तो तश२= तय१२+ तय२२ (d s2=d x2,+ d x22) समीकरण मिलेगा। किंतु समतल के स्थान पर वक्रतल हो, ता गौस ने यह सिद्ध किया कि इस वक्रतल पर यह लंबाई (अब यह लंबाई सरल रेखा नहीं रहेगी, वरन् वक्र रेखा होगी) निम्नलिखित समीकरण से प्राप्त होगी:
तश२= ग११तय१२+ ग१२, तय१ तय२+ ग२१, तय२तय१+ ग२२तय२२
(d s2=g11d x12+g12 d x1d x2+g21 d x2d x1+g22d x22)...................................... (2)
यदि समतल, गोलीय, दीर्घवृत्तीय इत्यादि प्रकार के तल दिए जाएँ, तो इन 'ग' (g) की मात्राओं में उचित परिवर्तन करना होगा। गोलीय पृष्ठ के लिय (जैसा पृथ्वी का होता है) अब यूक्लिडीय भूमिति के सिद्धांत उचित नहीं रहेंगे। प्राय: त्रिविमितीय दिक् के लिए
तश२= S नम गनम तयन तयन [d s2=S nmgnm d xn d xm]
समीकरण मिलता है। इन गनम (gnm) को भिन्न भिन्न मूल्य देकर अनेक प्रकार के अयूक्लिडीय दिक् मिलते हैं। इस प्रकार यूक्लिडीय ज्यामिति की तर्कसंमत विधि का ही पालन करके बहुविमितीय दिक् की ज्यामितियाँ प्रतिपादित हुई और उनका विकास हुआ। काल्पनिक होने से यद्यपि ये ज्यामितियाँ बुद्धि की कसरत सी ही दिखाई देती रहीं, तथापि आवश्यकता होने पर भौतिकी में इनका कभी भी उपयोग हो सकता था।
माइकेल्सन मौर्लि के प्रयोग (इसे देखें) से पहले पहल यह स्पष्ट हुआ कि दिक् और काल के गुण न्यूटन के धारणनुसार नहीं हैं। इस प्रयोग के फल का समर्थन मापनदंड के फ़िट्जेराल्ड आकुंचन की कल्पना करके ही हो सकता है, किंतु न्यूटनीय विश्व में दिक् का ऐसा आकुंचन होना अस्वाभाविक तथा असंभाव्य है। फ़िट्जेराल्ड के स्पष्टीकरण को आगे बढ़ाकर लोरेंट्स ने अपने रूपांतरण समीकरणों का विकास किया (देखें आपेक्षितवाद), जिनके अनुसार प्रकृति के नियम सापेक्ष गति के लिए भी अबाधित रहते हैं। इन सब फलों को एकत्रित करके आइन्स्टाइन ने विशिष्ट आपेक्षितावाद प्रस्तुत किया और दिक् तथा काल की धारणाओं में क्रांति हुई।
आपेक्षितावाद के अनुसार दिक् तथा काल स्वतंत्र सत्ताएँ नहीं हैं। भौतिक घटनाओं के लिए दिक्काल के अविभाज्य चतुर्विमितीय सांतत्यक (Continuum) की धारणा की जाए तो माइकेल्सन मौर्लि के फलों के साथ साथ अन्य फल भी सरलता से स्पष्ट होते हैं। प्रतिष्ठित भौतिकी में भी दिक् काल का सांतत्यक था, किंतु उसे दिक् और काल ऐसे दो, स्वतंत्र तथा निरपेक्ष विभाग थे। किंतु आपेक्षितावाद के अनुसार जो दिक्काल का सांतत्यक होता है उसके ऐसे स्वतंत्र विभाग नहीं हो सकते। अत: दिक् और काल स्वतंत्र सत्ताएँ नहीं हो सकतीं। वैसे ही दिक् और काल की धारणा निरपेक्ष नहीं हो सकती। दिक् और काल की धारणा निरपेक्ष नहीं हो सकती। दिक् अथवा लंबाई का मापन करते समय दो प्रेक्षक यदि एक दूसरे की सापेक्ष गति की स्थिति में हों, तो उनके फल भिन्न होंगे, अर्थात् दिक् निरपेक्ष नहीं हो सकता। वैसे ही फल काल के लिए भी मिलते हैं। दो घटनाएँ एक ही प्रेक्षक के लिए यदि समक्षणिक हों तो उस प्रेक्षक के सापेक्ष गतिमान दूसरे प्रेक्षक के लिए वे दो घटनाएँ समक्षणिक नहीं रहेंगी, अर्थात् किसी वास्तव घटना के दिक् और काल का मापन इन दो प्रेक्षकों के लिए समान नहीं रहेगा। अत: चिरप्रतिष्ठित भौतिकी में दिक् और काल जो स्वतंत्र तथा निरपेक्ष सत्ताएँ समझी जाती थीं वह धारणा भ्रममूलक है। किंतु ये फल नित्य व्यवहार में स्पष्ट नहीं हो सकते, क्योंकि गति के साथ दिक् और काल की गणनाओं में आपेक्षितावाद के अनुसार जो परिवर्तन होते हैं, वे व्यावहारिक गतियों के लिए उपेक्षणीय ही होते हैं (देखें आपेक्षितावाद)।
दिक्
और काल की
इस आपेक्षितावादीय
धारणा को गणित
से विकसित करने
पर उसकी यथार्थता
अधिक स्पष्ट होती
है। चतुर्विमितीय
सांतत्यक में दिक्
की तीन विमितियाँ
और काल की
चौथी विमिति
रहती है, किंतु
काल केवल क
ऐसा नहीं होता
है। काल का पद
![]() प्र
क ऐसा होता
है, जहाँ
प्र
क ऐसा होता
है, जहाँ ![]() काल्पनिक
संख्या है, प्र
= प्रकाश
वेग और क =
काल। अत: चतुर्विमितीय
सांतत्यक के चार
मूल अवयव (य१,
य२, य३, स)
होंगे, जहाँ स
=
काल्पनिक
संख्या है, प्र
= प्रकाश
वेग और क =
काल। अत: चतुर्विमितीय
सांतत्यक के चार
मूल अवयव (य१,
य२, य३, स)
होंगे, जहाँ स
= ![]() प्र क। सांतत्यक
में दो समीप
के बिंदुओं का
अंतर समीकरण
(१) के बदले निम्नलिखित
होगा :
प्र क। सांतत्यक
में दो समीप
के बिंदुओं का
अंतर समीकरण
(१) के बदले निम्नलिखित
होगा :
तश२= तय१२+ तय२२+ तय३२+ तस२= तय१२+ तय२२+ तय३२- प्र२क२
[x22x23d s2=d x12+d x22+d x32+d T2=d x12+d x22+d x23- c2d t2]..... (3)
प्रत्येक प्रयोग में अथवा भौतिक घटना के लिए, इस प्रकार के समीकरण का उपयोग करना होगा। समीकरण (३) लोरेंट्स के रूपांतरणों में निश्चर रहता है। इस समीकरण में न्यूटनीय दिक् के तीन अवयव (य१, य२, य३) सरलता से समझे जा सकते हैं, किंतु काल के साथ जो काल्पनिक संख्या आती है उसे साधारण व्यवहार में समझना कठिन होता है। भौतिकी में का उपयोग सभी प्रकार के तंरगसिद्धातों में बारंबार आता है, अत: भौतिकी की दृष्टि से का इस प्रकार किसी समीकरण से समाविष्ट होना अस्वाभाविक नहीं होता और ऐसे समीकरणों से प्राप्त फल प्रयोग द्वारा प्राप्त फलों से संगति रखते हैं।
विशिष्ट गणित के द्वारा आपेक्षिता की दिक् तथा काल की धारणा का जैसा स्पष्टीकरण होता है उससे मिकोविस्की के बहुविमितीय (मैनिफोल्ड) का उपयोग करके ज्यामितीय रीति से समझना कम कठिन होता है। इस बहुविमितीय में किसी बिंदु का निर्देश चार निर्देशांकों (य१, य२, य३, ज्ञ) से होता है, जहाँ य१, य२, तथा य३ पूर्वोक्त तीन विमितीय दिकों के तीन आयताकार निर्देशांक हैं और ज्ञ = काल � प्रकाशवेग = प्रक चतुर्थ निर्देशांक है। इस बहुविमितीय के प्रतयेक बिंदु को 'विश्वबिंदु' कहते हैं और वह भौतिक विश्व की एक घटना सूचित करता है। इसी प्रकार इस बहुविमितीय का वक्र क्रमिक घटनाओं को सूचित करता है और उसे 'विश्वरेखा' कहा जाता है। प्रत्येक विश्वरेखा एक द्रव्यविंद का मानो इतिहास सूचित करती है, क्योंकि उससे तीन विमितियों की भौतिक दिक् में, काल के साथ इस द्रव्यबिंदु के स्थान का जो विचलन होता है उसका निदर्शन होता है। ऐसी विश्वरेखाओं के समूह से भौतिक विश्व का इतिहास निदर्शित होता है।
सरलता के लिए हम समझेंगें कि घटनाएँ दिक् में केवल एक ही विमिति में हो रही है, जैसे ऋजु रेखीय गति। अब हमको केवल क्ष = य१ [x=x1] और 'ज्ञ' (c t) निर्देशांकों का ही विचार करना होगा।
चित्र (१) में दो संबद्ध अतिपरवलय दिखाए गए हैं, जिनके समीकरण निम्नलिखित हैं:
ज्ञ२- क्ष२= 1 (c2t2- x2=1)
ज्ञ२- क्ष२= - 1 [c2t2- x2=- 1]
वैसे ही दो अनंतस्पर्शी (asymptote) ज्ञ२- क्ष२= 0 [c2t2- x2= 0] इस समीकरण से मिलते हैं। अब अ मू ब और अ� मू ब� पादों में किसी भी
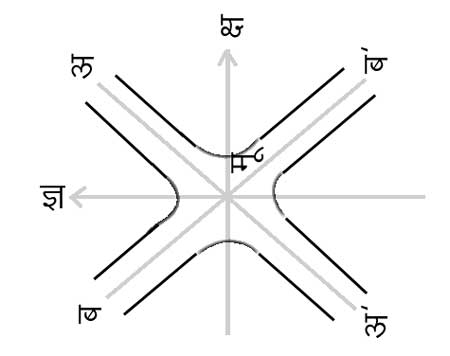
चित्र १.
बिंदु से जो घटना सूचित होगी, वह घटना उस द्रव्यकरण का प्रत्यक्ष वेग होगा, क्योंकि इन पादों में ।क्ष। � ।ज्ञ। यह प्रतिबंध होगा। विपेक्ष में ब� मू अ और अ� मू ब इन पादों में कोई भी बिंदु हो, तो व ऐसी
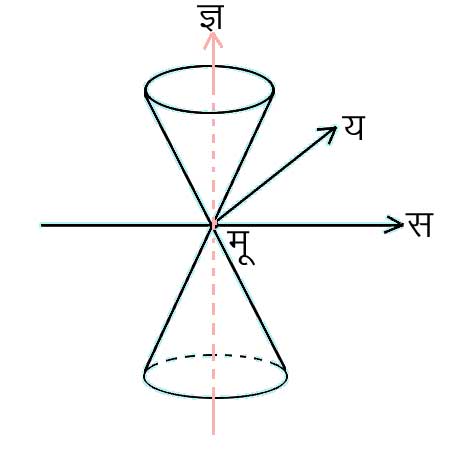
चित्र २.
घटना दिखाएगा जो द्रव्य कणों के लिए असंभाव्य है (अर्थात् यहाँ यह कल्पना की गई है कि द्रव्यकण क्ष = ० और ज्ञ = ० इस स्थिति से विचलित होते हैं)। यदि मूलबिंदु 'मू' को 'वर्तमान क्षण' समझा जाए तो ऋण 'ज्ञ' अक्ष पर गत क्षण होंगे और धन 'ज्ञ' अक्ष पर भविष्य क्षण होंगे। अफ़ मू अ अनंतस्पर्शी धन क्ष दिशा में प्रकाश की विश्वरेखा है।
यदि द्रव्यबिंदुओं की (क्ष, य) दो विमितीय गतियों का चिर करें ता 'प्रकाशशंकु' मिलता है (चित्र २), जिसका चित्र आपेक्षिता की पुस्तकों में दिया होता है।
मिंकाविस्की की इस व्याख्या से आपेक्षितावाद के अनुसार दिक् और काल की धारणाओं को समझने में तथा उनके गुणों का विकास करने में सहूलियत होती है। इस कल्पना से लोरेंट्स के रूपांतरण सरलता से प्राप्त होते हैं तथा स्वाभाविक भी दिखाई देते हैं। मिंकोविस्की के ही शब्दों में ''अब दिक् और काल की सत्ताएँ लुप्त हो जाएँगी, उनकी केवल छाया ही रहेगी और उनके स्थान पर उन दोनों के विशिष्ट मेल (संयोग) का ही अस्तित्व रहेगा।''
आपेक्षितावाद प्रणीत दिक् तथा काल की ये धारणाएँ पार्थिव प्रयोगों में पूर्णत: सफल रही हैं। दिक् काल के हमारे अनुभाव अब तक वस्तुत: पृथ्वी के पृष्ठ पर तथा आसपास के दिक् तक ही मर्यादित हैं, किंतु पृथ्वी से अतिदूर (करोड़ों प्रकाशवर्षों की दूरी पर) जो नीहारिकाएँ इत्यादि हैं, उनकी भी खोज विशाल प्रकाशकीय दूरदर्शी (जैसे माउंट पैलोमार की २०० इंच व्यास की दूरबीन), रेडिओ दूरदर्शी (जैसे जाडेल बैंक का २५० फुट का रेडियो दूरदर्शी) तथा अन्य अत्यंत संवेदी तथा प्रभावशाली उपकरणों से हो रही है। इन फलों से दिक् और काल की वर्तमान समय की हमारी धारणाएँ वैसी ही बनी रहेंगी, या उनमें परिवर्तन करना होगा, यह निश्चित रूप से नहीं कहा जा सकता। इतनी दूरी पर दिक् की वक्रता कितनी है, यह पर्याप्त रूप से विश्वासयोग्य फल प्राप्त होने पर ही कहा जा सकता है। (देवीदास रघुनाथराव भवालकर)