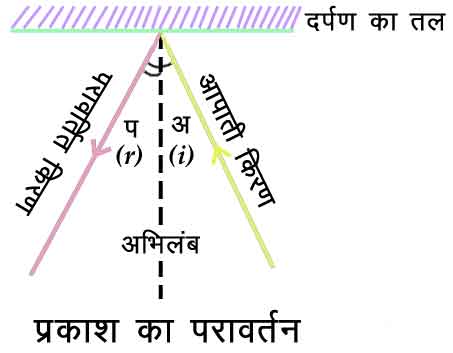
चित्र १. प्रकाश का परावर्तन
दर्पण (Mirrors) ऐसे प्रकाशीय तल (optical surfaces) हैं जो प्रकाश की किरणों के परावर्तन (reflection) के द्वारा या तो प्रकाशपुंज को प्रत्यावर्तित कर देते हैं अथवा उसे एक बिंदु पर अभिसृत (converge) करके बिंब (image) का निर्माण करते हैं। प्रकाशीय यंत्रों के, विशेष कर ज्योतिष से संबधित यंत्रों के, निर्माण में दर्पणों ने अत्यंत महत्वपूर्ण सहायता प्रदान की है। दर्पण के तल से परावर्तित होते समय प्रकाश की किरणें दो विशेष नियमों का पालन करती हैं। इन नियमों को परावर्तन के नियम (Laws of Reflection) कहते हैं। ये निम्नलिखित हैं:

चित्र १. प्रकाश का परावर्तन
किरणों की गति की दिशा तीरों से दिखाई गई है।
यदि कोई तल प्रकाश की किरणों का परावर्तन किसी ऐसे प्रकार से करता है जिसमें किरणें उपर्युक्त नियमों का पालन नहीं करतीं तो ऐसा तल दर्पण का तल न होकर विसारी परावर्तक तल (diffusive reflecting surface) कहा जाएगा।
प्राय: सभी दर्पणों की रचना समुचित आकृति के काचतल पर किसी अत्यधिक परावर्तनशील पदार्थ की पतली परत चढ़ाकर की जाती है। यह प्रक्रिया प्राय: निर्वात आलेपन द्वारा संपन्न की जाती है और पदार्थ का चयन उस वर्णक्रम प्रदेश के अनुसार किया जाता है जिसके लिय दर्पण का प्रयोग अभीष्ट है।
दृश्य प्रखंड (visible region) के लिए चाँदी सर्वाधिक परावर्तनीयता (reflectivity) प्रदान करती है, किंतु साधारणतया ऐल्यूमिनियम का ही उपयोग किया जाता है। इसका कारण यह है कि एल्यूमिनियम चाँदी की अपेक्षा अधिक टिकाऊ होता है। इसका कारण ऐल्यूमिनियम ऑक्साइड है, जो ऐल्यूमिनियम के वायुमंडल के संपर्क में आने पर बन जाता है।
निकटस्थ तथा दूरस्थ अवरक्त प्रखंड (Near and far infra-red region) - लगभग २म्यू (२m ) तरंगदैर्ध्य तक के प्रकाश के लिए ऐल्यूमिनियम के स्थान पर सोने का उपयोग दर्पण की कलई करने के लिए किया जाता है। ०.३५ म्यू (m ) के नीचे वर्णक्रम प्रखंड के लिए पुन: ऐल्यूमिनियम ही उपयुक्त सिद्ध होता है, क्योंकि ०.३१ म्यू (m ) के समीप की किरणों के लिए ऐल्यूमिनियम पारदर्शी होता है। ०.१० म्यू (m ) के नीचे प्लैटिनम का उपयोग किया जाता है, क्योंकि इन किरणों के लिए ऐल्यूमिनियम पारदर्शी होता है।
समतल दर्पण - समतल दर्पण द्वारा किसी वस्तु का बिंब बनने की प्रक्रिया में निम्नलिखित तीन बातें मुख्य होती हैं :
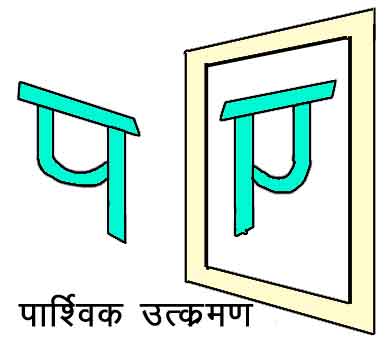
चित्र २. पार्श्विक उत्क्रमण
समतल दर्पण से बननेवाले बिंब प्रतीयमान (virtual) होते हैं, क्योंकि परावर्तित किरणें किसी एक बिंदु पर मिलती नहीं, वरन् बिंब से अपसृत (diverge) होती हुई प्रतीत होती हैं। इसलिए ये किरणें किसी पर्दे पर वस्तु के वास्तविक (real) बिंब का निर्माण नहीं कर सकतीं।
परस्पर झुके हुए दर्पणों से बिंबों का निर्माण - जब दो समतल दर्पण एक दूसरे पर झुके हुए होते हैं तब उनके बीच स्थित किसी वस्तु का बिंब दोनों दर्पणों द्वारा बनता है। इन बिंबों से और भी अनेक बिंब पुनरावृत परावर्तनों (repeated reflections) द्वारा बन सकते हैं,
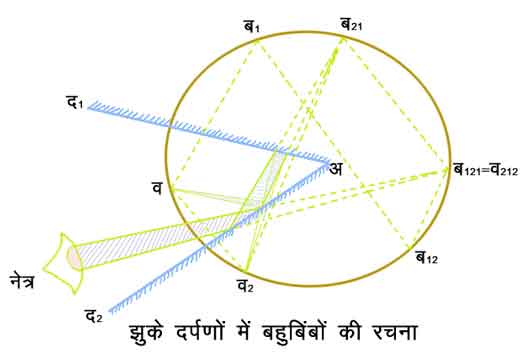
चित्र ३. झुके दर्पणों में बहुबिंबों की रचना
जिनकी संख्या उन दर्पणों के बीच के कोण पर निर्भर करती है। चित्र ३. में दो दर्पण परस्पर ६०° के कोण पर झुके हुए दिखलाए गए हैं। इनके बीच स्थित वस्तु व के बिंबों यथा ब१, ब२, ब१२, ब२१ और ब१२१ (= ब२१२) की स्थिति एवं रचनाप्रक्रिया भली भाँति समझाई गई है। यह स्पष्ट है कि सभी बिंब एक वृत्त की परिधि पर स्थित होंगे, जिसका केंद्र अ, दर्पणों की संधि पर है। जब एक ऐसा बिंब बन जाएगा जो दोनों दर्पणों के पीछे स्थित होगा तथा आगे परावर्तनों का क्रम बंद हो जाएगा। सामान्य रूप से दो झुके हुए दर्पणों द्वारा बननेवाले बिंबों की संख्या न निम्नलिखित सूत्र की सहायता से ज्ञात की जा सकती है :
![]()
जहाँ को (q ) दोनों दर्पणों के बीच का कोण है।
दर्पणों का घूर्णन (Rotation of mirrors) - किसी समतल दर्पण के यदि को (q ) कोण जितना घुमाया जाए, तो परावर्तित किरण २ को (२q ) कोण घूम जाती है। इसे नीचे दिए हुए चित्र ४. द्वारा आसानी से समझा जा सकता है। मान लिया दर्पण पहले क ख स्थिति में था। अ ब तथा ब स क्रमश: आपाती एवं परावर्तित किरणों की दिशाएँ हैं तथा न ब अभिलंब है। अत: Ð अ ब न = आपतन कोण अ (i) तथा Ð स ब न = परावर्तन कोण प (r)। मान लिया कि Ð को (q ) जितना घूमने पर दर्पण क¢ ख¢ स्थिति में आ जाता है, जिससे ब पर ब न अभिलंब, Ð न ब न= को (q ) जितना घूमकर, ब न¢ स्थिति में आ जाता है। अत: Ð अ ब न¢ उ नया आपतन कोण अ¢ (i¢ ) तथा Ð दबन¢ = नया परावर्तन कोण प¢ (r¢ ) है। Ð स ब द परावर्तित किरणों के बीच का कोण है।
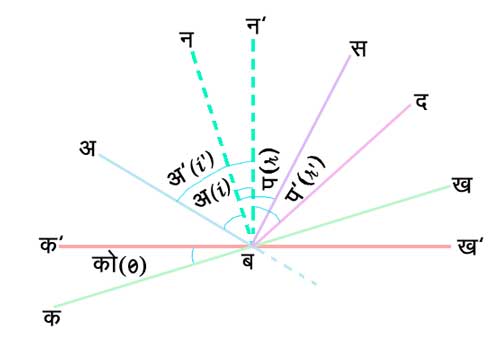
![]() Ð
अ ब न¢ =
Ð
द ब न¢
Ð
अ ब न¢ =
Ð
द ब न¢
या Ð अ अ Ð न ब न¢ = Ð प- Ð न ब न¢ + Ð द व स
या Ð अ + २Ð न ब न¢ - Ð प = Ð द ब स
चूँकि Ð अ = Ð प
\ २ Ð न ब न¢ = Ð द ब स
चूँकि Ð न ब न¢ = Ð को
\ २ Ð को = Ð द ब स
अर्थात् परावर्तित किरण में दर्पण के घुमाव का दुना घुमाव उत्पन्न हो जाता है।
गोलीय दर्पण (Spherical mirrors) - किसी वस्तु से आनेवाली प्रकाश की किरणों को अभिसृत कर उस वस्तु का वास्तविक बिंब बनाने के लिए गोलीय दर्पण प्रयुक्त होते हैं। किसी गोले (sphere) के एक भाग को काटकर अलग कर दिया जाए (चित्र ५. में छायादार भाग) और उसे पूर्वोक्त विधि से परावर्तंक बना दिया जाए ता गेलीय दर्पण का निर्माण हो जाता है। यदि इस भाग के अवतल तल को परावर्तक बना दिया जाए तो अवतल (concave) और यदि उत्तल तल को परावर्तक बना दिया जाए तो उत्तल (convex) दर्पण की रचना होती है। किसी गोलीय दर्पण के बीच के
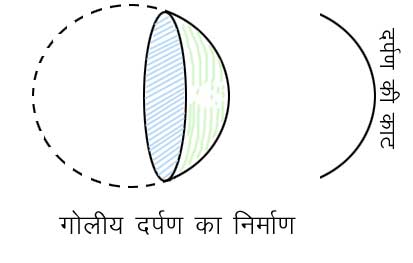
चित्र ५. गोलीय दर्पण का निर्माण
दाहिनी ओर दर्पण की काट दिखाई गई है।
बिंदु ध (चित्र ६.) से दर्पण के तल के लंबवत् कल्पित रेखा को दर्पण का मुख्य अक्ष (Principal axis) तथा बिंदु को ध्रुव (Pole) कहते हैं। जिस गोले का दर्पण एक भाग होता है उसके केंद्र स को गोलीय दर्पण का वक्रता केंद्र (Centre of curvature) कहते हैं। ध्रुव से वक्रताकेंद्र की दूरी को वक्रता अर्धव्यास (Radius of curvature) कहते हैं। इन दो बिंदुओं के ठीक बीच में अक्ष पर स्थित बिंदु क को दर्पण का फोकस (Focus) तथा ध्रुव से फोकस की दूरी को फोकस अंतर (Focal length) कहते हैं। मुख्य अक्ष के समांतर आनेवली समस्त आपाती किरणें दर्पण से परावर्तन के उपरांत फोकस से होकर जाती हैं।
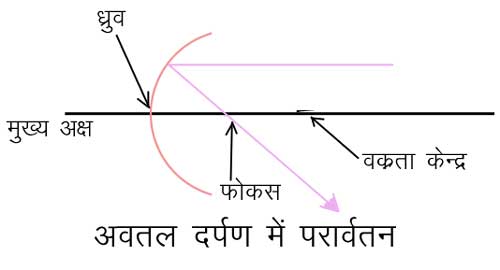
चित्र ६. अवतल दर्पण में परावर्तन
मुख्य अक्ष के समांतर प्रकाश की किरण का परावर्तन दिखाया गया है। ध ध्रुव, क फोकस तथा स वक्रता केंद्र।
इन दर्पणों से बिंबों की स्थिति एवं आकार प्रकार का अध्ययन करते समय यह ध्यान रखना चाहिए कि (१) सभी दूरियाँ ध्रुव से नापी जाती हैं और (२) आपाती किरण की दिशा में नापी गई दूरियाँ ऋणात्मक तथा विपरीत दिशा में नापी गई दूरियाँ धनात्मक होती हैं। चिह्नों के इन नियमों को ध्यान में रखते हुए ध्रुव से वस्तु की दूरी उ (u), बिंब की दूरी व (v), वक्रता अर्धव्यास र (r) तथा फोकस अंतर फ (f) के बीच संबंध निम्नलिखित सूत्र द्वारा व्यक्त किया जा सकता है:
![]()
बिंब और वस्तु के आकारों की निष्पत्ति को आवर्धन (magnification) कहते हैं और यह निष्पत्ति ध्रुव से बिंब और वस्तु की दूरियों की निष्पत्ति के बराबर होती है, अर्थात्
![]()
अवतल और उत्तल दर्पणों से बननेवाली बिंबों की स्थिति, प्रकृति एवं आकार का ज्ञान नीचे दी हुई सारणी के द्वारा सुगमता से हो सकता है। इस सारणी में स, क, ध, इत्यादि बिंदु चित्र ६. के अनुसार ही हैं।
|
दर्पण |
वस्तु की स्थिति |
बिंब की स्थिति |
बिंब का आकार |
बिंब उल्टा या सीधा |
बिंब वास्तविक या प्रतीयमान |
|
|
अनंत पर |
फोकस पर |
अत्यंत छोटा |
उल्टा |
वास्तविक |
|
|
अनंत और स के बीच में |
क और स के बीच में |
वस्तु से छोटा |
उल्टा |
वास्तविक |
|
|
स पर |
स पर |
वस्तु के बराबर |
उल्टा |
वास्तविक |
|
अवतल |
स और क के बीच में |
स और अनंत के बीच |
वस्तु से बड़ा |
उल्टा |
वास्तविक |
|
|
क पर |
अनंत पर |
अपरिमेय रूप से विशाल |
-- |
-- |
|
|
क और घ के बीच में |
दर्पण के दूसरी ओर |
वस्तु से बड़ा |
सीधा |
प्रतीयमान |
|
उत्तल |
कहीं भी |
दर्पण के दूसरी ओर |
वस्तु से बड़ा |
सीधा |
प्रतीयमान |
अगोलीय (Non-spherical) दर्पण - गोलीय दर्पणों से विपथनमुक्त (unaberrated) बिंब केवल उनके वक्रताकेंद्र पर ही बनता है। प्राय: अन्य सभी शंकुकाटों (conic sections) के इसी प्रकार के प्रकाशीय गुण होते हैं और इन्हीं गुणों के आधार पर उनका प्रकाशीय महत्व नियत किया जाता है। परवलय (parabola) का गुण होता है कि उसके फोकस से चलने वाली सभी किरणें परावर्तन के उपरांत अक्ष के समांतर चली जाती हैं। इस गुण के उपयोगार्थ परवलयज (paraboloidal) दर्पणों का निर्माण किया जाता है। अत्यंत दीर्घ बिंबांतरों (image distances) के लिए इनका उपयोग किया जाता है।
इसी प्रकार दीर्घवृत्त (ellipse) के इस ज्यामितीय गुण का, कि इसके एक फोकस पर स्थित वस्तु का सुतीक्ष्ण बिंब दूसरे फोकस पर बनता है, उपयोग दीर्घवृत्तजीय (ellipsoidal) दर्पण के निर्माण में किया जाता है। लगभग यही विशेषता अतिपरवलयज (Hyprboloidal) दर्पण में भी पाई जाती है। अंतर इतना मात्र होता है कि दीर्घवृत्तजीय दर्पणों में काल्पनिक वस्तु का बिंब प्रतीयमान और वास्तविक वस्तु का बिंब वास्तविक होता है, किंतु अतिपरवलयज दर्पणों द्वारा वास्तविक वस्तु का प्रतीयमान बिंब और काल्पनिक वस्तु का वास्तविक बिंब बन जाता है।
उच्चसामर्थ्य संपन्न दूरदर्शियों (telescopes) तथा अन्य अनेक प्रकाशीय यंत्रों में दर्पणों का उपयोग किया जाता है। दुर्गम चोटियों, शिखरों एव आकाशीय पिंडों की ऊँचाइयाँ नापने के लिए व्यवहृत यंत्र, सेक्सटैंट (sextant), में समतल दर्पणों का उपयोग होता है। विशेषकर सुदीर्घ फोकस अंतरवाली प्रकाश-यंत्र-प्रणालियों में परवलयज, दीर्घवृत्तजीय तथा अतिपरवलयज दर्पणों का उपयोग किया जाता है। इनके कुछ दृष्टांत निम्नलिखित हैं:
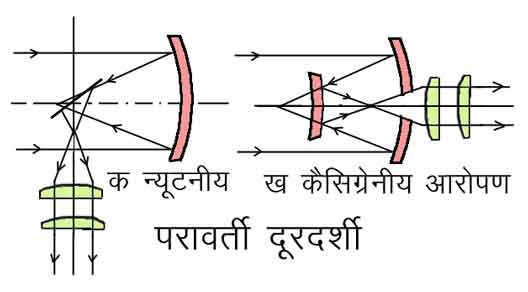
चित्र ७. परावर्ती दूरदर्शी
क. न्यूटनीय तथा ख. कैसिग्रेनीय आरोपण।
न्यूटनीय दूरदर्शी (Newtonian telescope) में परवलयज दर्पण का प्रयोग किया जाता है।
कैसिग्रेनीय (Cassegranian) दूरदर्शी में एक परवलयज तथा एक अतिपरवलयज दर्पण परस्पर इस प्रकार स्थित रहते हैं कि अतिपरवलयज का एक फोकस तो परवलयज के एक फोकस पर पड़ता है और दूसरा फोकस परवलयज के निकट ही स्थित होता है। फलस्वरूप, परवलयज द्वारा निर्मित प्रतीयमान बिंब अतिपरवलयज द्वारा वास्तविक बिंब में परिणत कर दिया जाता है।
ग्रेगोरियन (Gregorian) दूरदर्शी में एक दीर्घवृत्तजीय तथा एक परवलयज दर्पण का प्रयोग होता है। दीर्घवृत्तजीय को परवलयज के फोकस बिंदु से काफी दूर पर रखा जाता है और उसका एक फोकस परवलयज के ही फोकस पर पड़ता है। उसका दूसरा फोकस परवलयज के निकट ही पड़ता है। इस व्यवस्था में परवलयज द्वारा निर्मित प्राथमिक बिंब से दीर्घवृत्तजीय, एक द्वितीयक बिंब काफी दूर बनता है। (सु.चं.गौ.)