त्रिकोणीय सर्वेक्षण (Triangulation) उस विधि का नाम है जिसमें ज्ञात दूरी पर स्थित किन्हीं भी दो बिंदुओं से किसी तीसरे ऐसे बिंदु की सही सापेक्ष स्थिति निर्धारित की जाए जो ज्ञात बिंदुओं के साथ सुघटित त्रिभुज बनाए और उस त्रिभुज के तीनों कोण ज्ञात कर लिए गए हों। यदि ऐसे त्रिभुज की एक, दो या तीनों भुजाओं पर क्रमानुगत त्रिभुज बनाते चले जाएँ और प्रारंभिक त्रिभुज की एक भुजा, उसके दोनों शीर्ष बिंदुओं के नियामक और बनाए गए सभी त्रिभुजों के कोण ज्ञात हों, तो ऐसी संपूर्ण त्रिभुज माला की भुजाओं की लंबाइयाँ और त्रिभुज बनानेवाले बिंदुओं के नियामक और बनाए गए सभी त्रिभुजों के कोण ज्ञात हों, तो ऐसी संपूर्ण त्रिभुज माला की भुजाओं की लंबाइयाँ और त्रिभुज बनानेवाले बिंदुओं के नियामक गणितीय कलन (computations) से ज्ञात किए जा सकते हैं। किसी भी क्षेत्र का मानचित्र बनाने के लिये इस प्रकार के बिंदु संपूर्ण क्षेत्र में समन रूप से बिखरें हुए स्थापित करना आवश्यक होता है। ऐसे बिंदुओं को सामूहिक रूप में सर्वेक्षण हेतु नियंत्रण ढाँचा और प्रत्येक बिंदु को अलग अलग सर्वेक्षण स्टेशन कहते हैं। सामान्यत:, जहाँ दो दूर के बिंदुओं के बीच सीधी दूरी नाप पाना संभव न हे, मगर वे आपस मे दृष्टिगत हों, वहाँ त्रिकोणीय सर्वेक्षण बड़ा लाभप्रद होता है।

जिस क्षेत्र में सर्वेक्षण करना हो उसमें यदि दो बिंदु ऐसे उपलब्ध हों जो परस्पर दृष्टिगोचर हों और उनके नियामक ज्ञात हों तो एक तीसरा समुचित बिंदु चुनकर प्रारंभिक त्रिभुज उसपर बनाया जा सकता है। किसी भी त्रिभुजमाला में आरंभ करने के लिये एक भुजा ज्ञात होना आवश्यक है। ऐसी भुजा को आधाररेखा कहते हैं। आधार-रेखा के सिरे के बिंदुओं के नियामक ज्ञात हों, तो गणना द्वारा उसकी लंबाई निकाली जा सकती है। उदाहरणार्थ, यदि उन बिंदुओं के नियामक मूलबिंदु (origin) से उत्तर-दक्षिण रेखा, कोटि (ordinate), पर क्रमश: उ_१ (N₁), उ_२ (N₂), तथा पूर्व-पश्चिम रेखा, भुज (abscisaa), पर पू_१ (E₁), पू_२ (E₂) हों तो भुजा की होगी। उस भुजा का उत्तर दिशा से दक्षिणवर्ती कोण (clockwise angle)

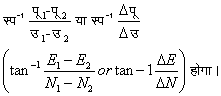
इस कोण की आवश्यकता नियामकों की गणना में होती है। इसे दिङ्मान (bearing) कहते हैं।

यदि ऐसे दो बिंदु उपलब्ध न हों तो आधार उसी समय नापकर स्थापित किया जाता है। इसके लिये सर्वेक्षक आरंभ करने वाले बिंदु के आसपास एक सुविधाजनक समतल भूखंड पर, यथार्थ माप देनेवाले फीते से, एक रेखा अ आ नापता है। आजकल मुख्यत: यह नाप फीते को रज्जुवक्र (catenary) में टाँग कर लेते हैं। फीते के सिरों के बीच यथार्थ क्षैतिज दूरी गणना द्वारा निकाल ली जाती है। उस पर क्रमश: ऐसे त्रिभुज बनाए जाते हैं कि पहले एक या दो त्रिभुजों को छोड़कर किसी भी त्रिभुज का कोई भी कोण २०°से कम न हो। आधार भुजा से आरंभ करते समय दो कोण इ और ई ३°तक के ले लिए जाते हैं। मगर इन्हें आवृत्ति विधि (method of repetition) से बहुत ही यथार्थ नापते हैं।

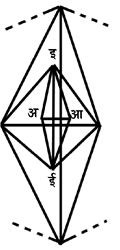
चित्र ३

यह कोण थियोडोलाइट नामक यंत्र से नापते हैं। आधार बिंदुओं से आरंभ करके क्रमश: सभी स्टेशन बिंदुओं पर थियोडोलाइट केंद्रित करके कोण पढ़ लिए जाते हैं। जैसे जैसे त्रिभुजमाला के एक एक त्रिभुज या चतुर्भुज के सारे कोण पूरे हो जाते हैं, सर्वेक्षक ज्यामितीय संबंधों, जैसे त्रिभुज के तीनों कोण (१८०°) या चतुर्भुज के चारों कोण (३६०°), की जाँच करता जाता है। पृथ्वी की सतह गोलाकार होने के कारण त्रिभुज बहुत बड़े होने पर उसके कोणों का योग १८०° से अधिक हो जाता है। इस प्रकार की बढ़ती को गोलीय आधिक्य (spherical excess) कहते हैं। ७५ वर्ग मीलवाले त्रिभुज में यह आधिक्य १'' होता है। प्रेक्षण त्रुटियों और गोलीय आधिक्य का शोधन करके गणना में कोण प्रयुक्त होते हैं।

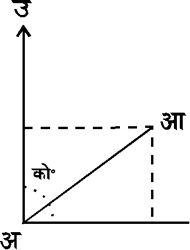से सभी भुजाओं की लंबाइयाँ ज्ञात हो जाती हैं। तदुपरांत नियामक निकालने के लिये ज्ञात बिंदु या बिंदुओं से अज्ञात बिंदु को जोड़ने वाली रेखा या रेखाओं के दिङ्मान, जिसका उल्लेख पहले हो चुका है, निकाल लिए जाते हैं। ज्ञात बिंदु या बिंदुओं से अज्ञात बिंदु की दूरी द (d) और को (b) दिङ्मान ज्ञात होने से उसके नियामक उ+द कोज्या को और पू+द ज्या को ज्ञात किए जा सकते हैं। ये आयताकार नियामक कहलाते हैं। यदि ऊर्ध्व कोण भी क्षैतिज प्रेक्षण के साथ पड़ जाएँ तो अज्ञात बिंदु की ऊँचाई ऊ+ द स्प न होगी। उपर्युक्त समीकरणों में उ, पू और ऊज्ञात बिंदु की क्रमश: उत्तरायण तथा पूर्वायण ऊँचाइयाँ हैं और द एवं न क्रमश: अज्ञात बिंद की दूरी और नतिकोण हैं। पृथ्वी को गोलाभ मानकर बिंदुओं के भौगोलिक नियामक, अर्थात् अक्षांश और देशांतर, भी निकले जा सकते हैं।

यदि किसी क्षेत्र में सर्वेक्षण पहली बार आरंभ हो रहा हो, जहाँ काई भी बिंदु ज्ञात न हो तो कुछ दिन तक निरंत खगोलीय प्रेक्षण करके एक बिंदु के नियामक निर्धारित करते हैं। रात के समय स्वच्छ आकाश को दिन प्रति दिन देखने से विदित होगा कि बहुतेरे पहचानने योग्य चमकीले तारे समान रूप से एक गोले की सतह पर तैरते से दिखाई देते हैं। उनके उदय और अस्त भी नियमित रूप से होते देखे जाएँगे। ऐसे गोले को भी पृथ्वी की भाँति याम्योत्तरों और समांतरों से बँटे होने की ग्राह्य कल्पना की जा सकती है, जो गणितीय सूत्रों का पालन करती है। इन तथ्यों का लाभ उठाकर सर्वेक्षक तारों का प्रेक्षण करके प्रेक्षण स्टेशन के नियामक निकालने में सफल हो जाता है। उससे और नापी हुई अधाररेखा से त्रिकोणीय सर्वेक्षण किया जा सकता है। [गुरुनारायण दूबे]