त्रिकोणमिति इस विज्ञान के आविर्भाव तथा विकास का कारण उन कोणों और दूरियों की संख्यात्मक माप ज्ञात करने की जिज्ञासा है, जिनको मापने के लिये समतल ज्यामिति में किसी विशेष पैमाने पर आरेखों की आवश्यकता पड़ती है। इस विज्ञान के अध्ययन का विषय कोणों के फलनों (functions) की सहायता से किसी समतल में स्थित ज्ञात कोणों और दूरियों के आधार पर, उसी समतल, अथवा किसी अन्य समतल में स्थित, अज्ञात कोणों और दूरियों की मापों को निर्धारित करना है।
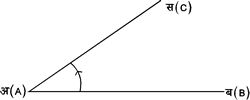
कोणों की व्यापक संकल्पना (General Conception of Angles) -- किसी एक बिंदु पर एक सरल रेखा के परिक्रमा करने से कोण बनता है। जब सरल रेखा वामावर्त परिक्रमा करती है तब कोण धनात्मक होता है और जब सरलरेखा दक्षिणवर्त परिक्रमा करती है तब कोण ऋणात्मक होता है।

चित्र १
Ð ब अ स (B A C), चित्र १. में धनात्मक तथा चित्र २. में ऋणात्मक है। किसी कोण की संख्यात्मक माप परिक्रामी रेखा (revolvin line) के घुमाव की मात्रा पर निर्भर है, अर्थात् परिक्रामी रेखा की आदि तथा अंतिम स्थितियाँ कोण की संख्यात्मक माप सूचित करती हैं। दो कोण उसी दशा में समान होते हैं, जब उनके परिमाण समान हो और उनकी दिशाएँ भी एक ही हो।
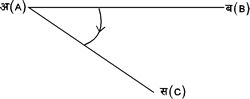
चित्र २
मान लिया किसी सरल रेखा की आदिस्थिति अ ब (A B) है। यह रेखा बिंदु Ðअ (A) के बराबर है। फिर चित्र ३. में वामावर्त और चित्र ४. दक्षिणावर्त चलकर अ द (A D) पर रुक जाती है। ऐसा करने से वह Ðस अ द (C A D) बनाती है, जो परिमाण में Ðब (B) के बराबर है। चित्र ३. में Ðस अ द (C A D) = + ब (B) और चित्र ४. में Ðस अ द (C A D) = -ब (-B)। अत: चित्र ३. में Ðब अ द (BA D) अ + ब (A + B) तथा चित्र म४ में Ðब अ द (B A D) = अ - ब (A - B)।
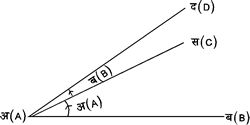
चित्र ३
कोणों की माप -- साधारणत: कोणों की माप करने की दो पद्धतियाँ हैं : (१) समाकोणिक और (२) वृत्तीय।
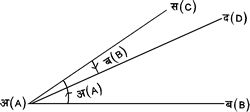
चित्र ४
(१) समकोणिक माप : मान लिया कि कोई परिक्रामी रेखा अपनी आदिस्थिति उ अ (O A) से आरंभ कर उ (O) पर वामावर्त परिक्रमा करती हुई एक पूरा चक्कर लगाती है, अर्थात् इस रेखा की आदि तथा अंतिम स्थिति एक ही हो जाती है। इस पूरे चक्कर के चार बराबर भागों में से प्रत्येक भाग को चतुर्थांश (Quadrant) कहते हैं और प्रत्येक चतुर्थांश की संख्यात्मक माप को समकोण कहते हैं। चित्र ५ में
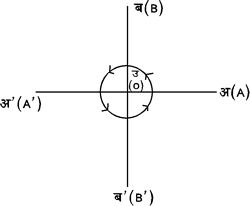
चित्र ५
Ðअ उ ब =Ðब उ अ' -Ð अ' उ ब' = ब' उ अ[ÐA O B = ÐB O A' = A' O B' = ÐB' O A]इस पद्धति में माप की इकाई समकोण है। समकोणिक पद्धति में कोणों की माप करने की दो रीतियाँ हैं : (क) षाष्ठिक (Sexagesimal) और (ख) शतिक (Centesimal)
(क) पौष्टिक रीति में एक समकोण = ९० अंश, १ अंश = ६० मिनट और १ मिनट = ६० सेकंड होता है। अंश (degree), मिनट और सेकंड के सांकेतिक चिह्न क्रमश: °, ' और '' हैं, जैसे ३६ अंश ४० मिनट और ४५ सेकंड को ३६°४०' ४५'' लिखते हैं।
(ख) शतिक पद्धति में एक समकोण १०० अंशक (grades) के बराबर है, १ अंशक = १०० मिनट और १ मिनट = १०० सेकंड। ग्रेड (अंशक), मिनट और सेकंड के सांकेति चिह्नअं (ड), ' और '' हैं। ३५अं (ड) ९६' ७५'' से ३५ अंशक ९६ मिनट और ७५ सेकंड समझा जाएगा।
२. वृत्तीय माप (Circular measurement) : इस पद्धति में माप की इकाई रेडियन (radian) है। वृत्त के उस चाप द्वारा, जिसकी लंबाई उसी वृत्त की त्रिज्या के बराबर है, उसी वृत्त के केंद्र पर अंतरित कोण के परिमाण को रेडियन कहते हैं। चित्र ६. में वृत अ ब स (A B C) का केंद्र उ (O) है, यदि चाप अ ब (A B) = उ अ (O A) = उ ब (O B), तब Ðअ उ ब (A O B) = एक रेडियन।
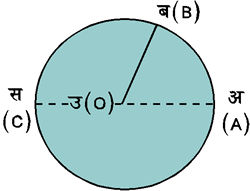
चित्र ६
रेडियन का सांकेतिक चिह्न रे (c) है। जैसे ८रे (८°) से ८ रेडियन समझा जाता है। परिक्रामी रेखा के एक पूरा चक्कर लगाने पर २p रेडियन का कोण बनता है। उपर्युक्त परिभाषा के अनुसार चार समकोण = 360° = ४००अं (ड) = 2p। स्मरण रहे कि p के ऊपर रेडियन का सांकेतिक चिह्न नहीं लगाया जाता।
जब परिक्रामी रेखा न (n) पूरे चक्कर लगाती है, तब कोण की संख्यात्मक माप = न ३६०° = ४००अं = २ न p
कभी कभी सैनिक विज्ञान में कोणों की माप की इकाई मिल (Mil) ली जाती है। इसमें
१,६०० मिल = एक समकोण = ९०°= १००अं
कोणों का त्रिकोण्मितीय फलन (Trigonmetric functions of angles) -- साधारणत: कोणों में निम्नलिखित छ: फलन हैं, जिनका उपयोग त्रिकोणमिति में किया जाता है :
ज्या (sine) या केवल (sin), कोटिज्या (cosine) या कोज्या (cos), स्पर्शज्या (tangent) या स्प (tan), व्युत्क्रमज्या (cosecant) या व्युज्या (cosec), व्युत्क्रमकोटिज्या (secant) या व्युको (sec) और कोटिस्पर्शज्या (cotangent) या कोस्प (cot)। कोणों के उपर्युक्त फलनों के त्रिभुल की भुजाओं के अनुपातों से व्यक्त करते हैं। जैसे, मान लिया कि समकोण त्रिभुज अ ब स (A B C) में Ðअ ब स (A B C) = ९०°तब
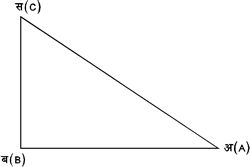
चित्र ७

उपर्युक्त अनुपातों से स्पष्ट है कि
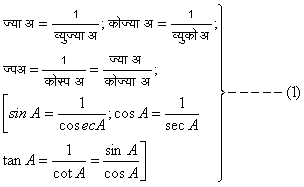
चित्र ७. में चूँकि अ ब२ + ब स२ = अ स२ (A B2 + BC2 = A C2) इसलिये
|
ज्या२ अ + कोज्या२ अ = १ [sin2 + cos2 A = 1]; १ + स्प२ अ = व्युको२ अ [1 + tan2 A = sec2 A]; १ + कोस्प२ अ = व्युज्या२ अ [1 + cot2 A = cosec2 A]; |
} | ---------------------(2) |
फिर चूँकि चित्र ७. में Ðअ (A) + Ðस (C) = ९०°= p/२, इसलिये :
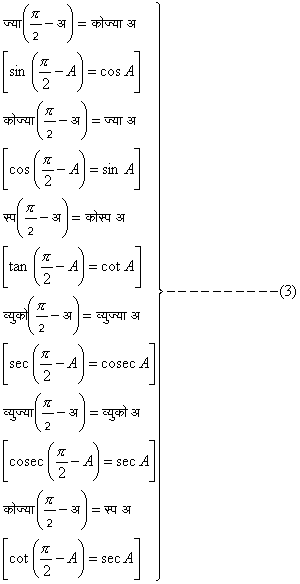
कोणों और उनके फलनों की परिभाषा की सहायता से यह दिखाया जा सकता है कि
 |
} | ---------------------(4) |
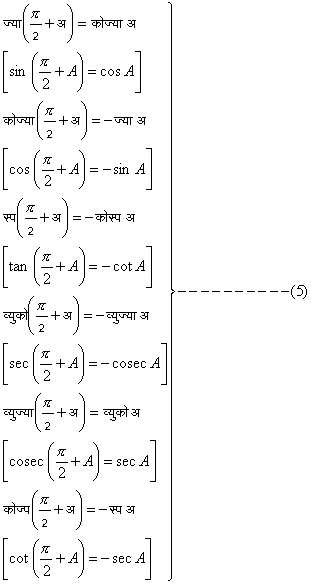
[sin (p`± A) = ±sin A]
कोज्या (p ± अ) = -कोज्या अ
[cos (p ± A) = -cos A]
स्प (p`+ अ) = -स्प अ
[tan (p`+ A) = -tan A]
व्युज्या (p`+ अ) = ±व्युज्या अ
[cosec (p`+ A) = ±cosec A]
व्युको (p`+ अ) = -व्युको अ
[sec (p`+ A) = -sec A]
कोस्प (p`+ अ) = -कोस्प अ
[cot (p`+ A) = -cot A]
श्
ज्या (२p`+ अ) =`+ज्या अ
[sin (2p`+ A) =`+sin A]
कोज्या (२p ± अ) = कोज्या अ
[cos (2p ± A) = cos A]
स्प (p`+ अ) =`+स्प अ
[tan (2p`+ A) =`+tan A]
व्युज्या (२p`+ अ) =`+व्युज्या अ
[cosec (2p`+ A) =`+cosec A]
व्युको (२p`+ अ) = व्युको अ
[sec (2p`+ A) = sec A]
कोस्प (२p`+ अ) =`+कोस्प अ
[cot (2p`+ A) =`+cot A]
श्
ज्या (२नp + अ) = ज्या अ
[sin (2np + A) = sin A]
कोज्या (२नp + अ) = कोज्या अ
[cos (2np + A) = coss A]
स्प (२नp + अ) = स्प अ
[tan (2np + A) = tan A]
व्युज्या (२नp + अ) = व्युज्या अ
[cosec (2np + A) = cosec A]
व्युको (२नp + अ) = व्युको अ
[sec (2np + A) = sec A]
कोस्प (२नp + अ) = कोस्प अ
[cot (2np + A) = cot A]
उपर्युक्त समीकरणों से स्पष्ट है कि :
(१) कोण अ (A) के कोटिपूरक कोण (complementary angles) का फलन अ (A) के संगत सहफलन (corresponding co-function) के बराबर होता है।
(२) किसी कोण के कोज्या और व्युको सम फलन (even function) हैं तथा अन्य चार त्रिकोणमितीय फलन विषम फलन (odd functions) हैं।
(३) किसी कोण के स्प तथा कोस्प का लघुत्तम आवर्तांक p और अन्य फलनों का लघुत्तम आवर्तांक = २p = ३६०°
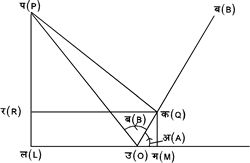
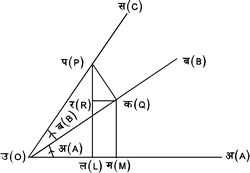
चित्र ९
चित्र ५. और ९. की सहायता से सिद्ध किया जा सकता है कि
|
ज्या (अ+ब) = ज्या अ कोज्या ब+कोज्या अ ज्या ब [sin (A+B) = sin A cos B + cos A sin B] |
} | -----------------------(9) |
|
कोज्या (अ+ब) = कोज्या अ कोज्या ब - ज्या अ ज्या ब [cos (A+B) = cos A cos B - sin A sin B] |
} | -----------------------(10) |
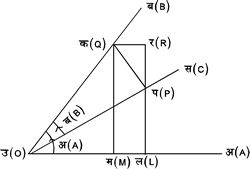
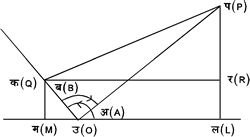
तथा चित्र १०. और ११. की सहायता से सिद्ध किया जा सकता है कि
 |
 |
|
चित्र
१०
|
चित्र ११ |
श्
|
ज्या (अ-ब) उ ज्या अ कौज्या ब - कोज्या अ ज्या ब [sin (A-B) = sin A cos B - cos A sin B] |
} | -----------------------(11) |
|
कोज्या (अ-ब) = कोज्या अ कोज्या ब + ज्या अ ज्या ब [cos (A-B) = cos A cos B + sin A sin B] |
} | -----------------------(12) |
श्
समीकरणों (९), (१०), (११) और (१२) की सहायता से यह दिखाया जा सकता है कि
५-५७

यदि समीकरणों (९), (१०) और (१३) में अ (A) = ब (B), तो
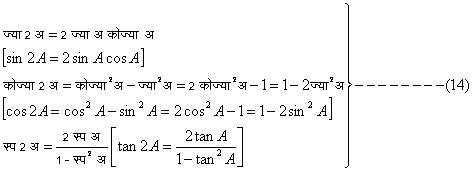
समीकरणों (९) और (१०) की सहायता से यह भी दिखाया जा सकता है कि
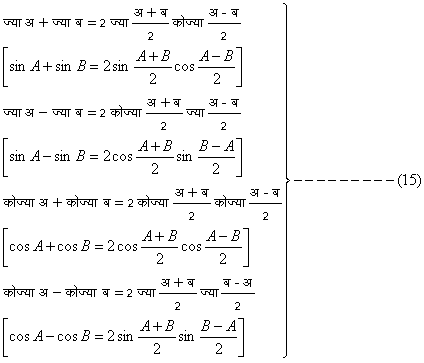
समीकरण (१४) से स्पष्ट है कि
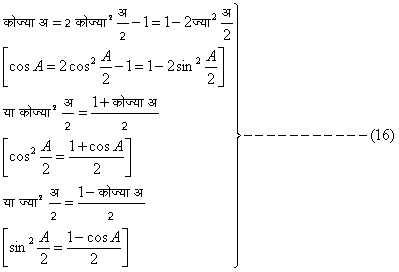
कुछ ज्ञात फलनों के नाम
|
अ (A) |
०° |
p /६ |
p /४ |
p /३ |
p /२ |
|
ज्या अ |
० |
१/२ |
१/Ö २ |
Ö ३/२ |
१ |
|
कोज्या अ |
१ |
Ö ३/२ |
१/Ö २ |
१/२ |
० |
|
स्प अ |
० |
१/Ö २ |
१ |
३ |
¥ |
|
व्युज्या अ |
¥ |
२ |
Ö २ |
२/Ö ३ |
१ |
|
व्युको अ |
१ |
२/Ö ३ |
Ö २ |
२ |
¥ |
|
कोस्प अ |
¥ |
Ö ३ |
१ |
१/Ö ३ |
० |
श्
इस सारणी तथा समीकरणों १, २, ३, ४, ५, ६, ७ तथा ८ की सहायता के किसी माप के कोण के फलन का मान ज्ञात किया जा सकता है।
समतल त्रिकोणमिति (Plane Trigonometry) -- अज्ञात दूरियों तथा कोणों को ज्ञात करने के लिये ऐसे त्रिभुज को हल किया जाता है जिसकी तीनों भुजाएँ एक ही समतल में स्थित होती हैं।
मान लिया कि चित्र १२. में D अ ब स (A B C) की भुजाएँ ब स (B C), स अ (C A) और अ ब (A B) की लंबाई क्रमश: क (a), ख (b) और ग (c) है, तथा इसके आधार ब स (B C) पर अ द (A D) लंब है और अ द (A D) = ऊँ(h) है।
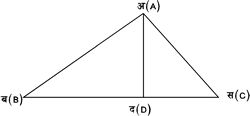
चित्र १२
D अ ब स (A B C) की भुजाओं की लंबाइयाँ, इसके कोणों की विभिन्न माप और इसके क्षेत्रफल की माप की अभिगणना में निम्नलिखित प्रमेयों की सहायता ली जाती है :
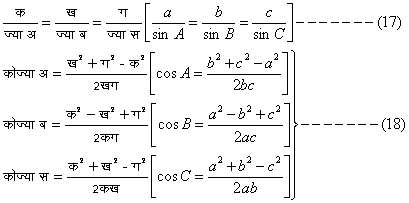
क ज्या ब = ख ज्या अ [a sin B = b sin A]}---------------------(20)
|
क = ग कोज्या ब = ख कोज्या स [a = c cos B + b cos C] |
--------------------------(21) |
D अ ब स (A B C) का क्षेत्रफल
|
= १/२ ख ग ज्या ब = १/२ ग क ज्या ब = १/२ क ख ज्या स [1/2 bc sin A = 1/2 c a sin B = 1/2 ab sin C] |
----------------------(22) |
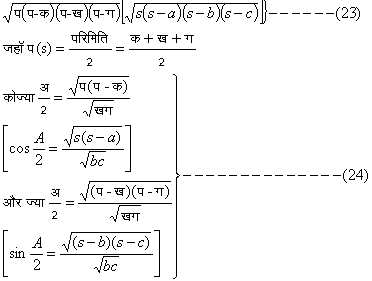
गोलीय त्रिकोणमिति (Spherical Trigonometry) -- अवकाश (space) की मूल संस्थिति (fundamental configuration), जिस पर गोलीय त्रिकोणमिति के सूत्र लागू होते हैं, एक बिंदु से निकलने वाली तीन किरणों से बना त्रितलीय कोण (trihedral angle) है। ये तीन किरणों तथा वह बिंदु जहाँ से ये विकीर्ण होती हैं, उस त्रितलीय कोण के क्रमश: तीनों कोर तथा शीर्ष हैं। इन किरणों में से प्रत्येक दो से निर्धारित समतल तथा कोण क्रमश: उन त्रितलीय कोण के फलक तथा फलक कोण हैं। फलकों में से प्रत्येक दो फलक से द्वितल कोण बनते हैं।
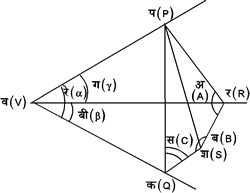
चित्र १३
चित्र १३. में शीर्ष बिंदु व (V) से निकलने वाली तीन किरणों व प (V P), व क (V Q) और व र (V R) हैं। इसमें ऐ (a), बी (b) और गा (g) फलक कोण हैं, और इनके संमुख बने द्वितल कोण क्रमश: अ (A), ब (B) और स (C) हैं।
मान लिया कि समतल प क श (PQS) तथा प र श (PRS) क्रमश: कोर व क (V Q) और व र (V R) पर लंब हैं। तब

(२५) को ज्या का नियम (law of sines) कहते हैं।
चित्र १४. में समतल प क र (P Q R) कोर व प (V P) पर लंब है।
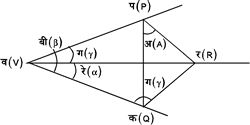
D प क र (P Q R) और D व क र (V Q R) में क्रम से
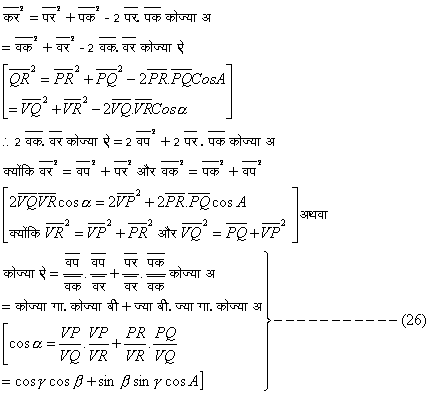
(२६) को कोज्या का नियम (Law of Consines) कहते हैं।
यदि त्रितलीय कोण के शीर्ष से इसके भीतरी फलकों पर लंब खींचे जायँ, तो दूसरा त्रितलीय कोण उत्पन्न हो जाएगा। दूसरे त्रितलीय कोण को पहले त्रितलीय कोण का ध्रुवी त्रितलीय कोण (polar trihedral angle) कहते हैं। ध्रुवी त्रितलीय कोण के फलककोण ऐ' (a') बी' (b') और गा' (g') क्रम से द्वितलकोण अ (A) ब (B) और स (C) के पूरक (supplementary) हैं।
\ कोज्या ऐ' = कोज्या (च - अ) = - कोज्या अ
[cos a' = cos (p - A) = - cos A]
\ (२६) में समीकरण से
कोज्या अ = - कोज्या ब कोज्या स + ज्या ब ज्या स कोज्या ऐ'
[cos A = - cos B cos C + sin B Sin C cos a']
गोलीय त्रिभुज (Spherical Triangle) -- यह त्रिभुज एक गोले के तल पर बनता है। इस त्रिभुज के शीर्षों को जब गोले के केंद्र उ (O) से मिला दिया जाता है, तब उ (O) पर एक त्रितलीय कोण बनता है, जैसा चित्र १५. में दिखाया गया है।
त्रितलीय कोण के फलक कोणों ऐ (a), बी (b) और गा (g) द्वारा बृहद्वत्त में से काटे गए खंड क्रमश: D अ ब बस (A B C) की भुजाएँ क (a), ख (b) और ग (c) हैं, तथा इसके कोण अ (A), ब (B) और स (C) त्रितलीय कोण के द्वितल कोण हैं।
चूँकि ध्रुवी त्रितलीय कोण के फलक गोले को दिए हुए त्रिभुज को ध्रुवी त्रिभुज में काटते हैं, इसलिये कोण संबंधी ज्या नियम (२५) और कोज्या नियम (२६) इस त्रिभुज पर भी लागू हैं।
(२५) से
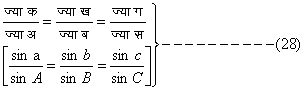
(२६) से
कोज्या क = कोज्या ख. कोज्या ग + ज्या ख. ज्या ग. कोज्या अ
[cos a = cos b. cos c + sin b. sin c. cos A]
कोज्या ख = कोज्या ग. कोज्या क + ज्या ग. ज्या क. कोज्या ब
[cos b = cos c. cos a + sin c. sin a. cos B]
कोज्या ग = कोज्या क. कोज्या ख + ज्या ख. ज्या क. कोज्या स
[cos c = cos a. cos b + sin b. sin a. cos C]
श्
और (२७) से
कोज्या अ = - कोज्या ब. कोज्या स + ज्या ब. ज्या स. कोज्या क
कोज्या ब = - कोज्या स. कोज्या अ + ज्या स. ज्या अ. कोज्या ख
कोज्या स = - कोज्या अ. कोज्या ब + ज्या अ. ज्या ब. कोज्या ग
[cos A = - cos B. cos C + sin B. sin C. cos a]
[cos B = - cos C. cos A + sin C. sin A. cos b]
[cos C = - cos A. cos C + sin A. sin B. cos a]
श्
गोलीय त्रिभुज अ ब स (A B C) का क्षेत्रफल
= ई त्रि२ (Er2), ........ (३१)
जहाँ ई (E) = अ + ब + स - p (A + B + C - p) और त्रि (r) = गोले की त्रिज्या।
जब Ðस (C) = ९०°, तब D अ ब स (A B C) को समकोण गोलीय त्रिभुज कहते हैं और तब समीकरण (२८), (२९) तथा (३०) से :
ज्या क = ज्या स. ज्या अ = स्प ख. कोस्प ब
[sin a = sin C. sin A = tan b. cot B]
ज्या ख = ज्या स. ज्या ब = स्प क. कोस्प अ
[sin b = sin C. sin B = tan a. cot A]
कोज्या अ = ज्या ब. कोज्या क = स्प ख. कोस्प स
[cos A = sin B. sin a = tan b. cot C]
कोज्या ब = ज्या अ. कोज्या ख = स्प क. कोस्प स
[cos B = sin A. sin b = tan a. cot C]
उपर्युक्त समीकरणें (२८), (२९), (३०), (३२) और (३२) ही सहायता से गोलीय त्रिभुज हल किए जाते हैं।
वैश्लेषिक त्रिकोणमिति (Analytic Trigonometry) -- यदि य (x) वास्तविक हो और इसकी माप रेडियन में दी हो, तो
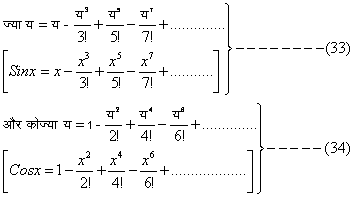
(३३) और (३४) की सहायता से किसी अंश के कोण की ज्या तथा कोज्या की गणना की जा सकती है। मान लिया ज्या २०°(sin 20°) का मान ज्ञात करना है।
\ २०° = p/९ रेडियन, इसलिये ३३वें समीकरण में य (x) के लिये p/९ प्रतिस्थापित करने से ज्या २०° (sin 20°) का मान ज्ञात हो जायगा।
सारणी १. की सहायता से त्रिकोणमितीय फलनों (functions) के आरेख नीचे दिए जाते हैं।
चित्र १६
ये चित्र त्रिकोणमितीय फलनों के केवल एक आवर्तांक (period) का आरेख प्रदर्शित करते हैं।
संमिश्र चर (Complex Variable) का त्रिकोणमितीय फलन -- चूँकि श्रेणियाँ (३३) और (३४) सभी संमिश्र संख्याओं (complex number) के लिये अभिसृत (converage) होती हैं, इसलिये इनका प्रयोग त्रिकोणमितीय फलन ज्या ल (sin Z), और कोज्या ल (cos Z) को परिभाषित करने के लिये किया जा सकता, जहाँ ल (Z) संमिश्र चर है। इस अवस्था में स्प ल (tan Z), कोस्प ल (cot Z), व्युज्या ल (cosec Z) और व्युकोज्या ल (sec Z) की परिभाषा क्रमश: निम्नलिखित फलनों द्वारा की जाती है :

समिश्र संख्याओं के क्षेत्र में त्रिकोणमितीय फलनों और घातीय श्रेणियों (exponentional series) में एक निकट संबंध है, क्योंकि
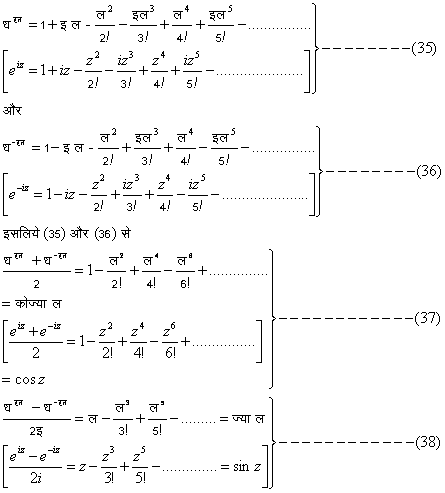
(३७) और (३८) से प्राप्त होनेवाले अनेक रुचिकर सूत्रों में डी मॉयवर के प्रमेय (De Moiver's theorem) का प्रमुख स्थान है। इस प्रमेय के अनुसार :
(कोज्या ल + इ ज्या ल)न = कोज्या न ल + इ ज्या न ल
[(cos z + i sin z)n = cos n z + i sin n z]
प्रतिलोम (inverse) त्रिकोण्मितीय फलन --यदि ज्या अ = क (sin A = a)
तो ज्या-१ क = अ (sin-1 a = A)
यदि कोज्या अ = ख (cos A = b)
तो कोज्या-१ ख = अ (cos-1 b = A)
यदि स्प अ = ग (tan A = c)
तो स्प-१ ग = अ (tan-1 c = A)
इसी प्रकार से अन्य फलन भी परिभाषित किए जाते हैं।
त्रिकोणमितीय बहुपदीय फलन और श्रेणियाँ --
यदि अ उ म ज्या ऐ, (A = M sin a,)
ब उ म कोज्या ऐ (B = M cos a)
तथा यदि म (M) और ओ (w) घनात्मक हों तो
म ज्या (ओ य + ऐ) = अ कोज्या ओ य + ब ज्या ओ य
[M sin (w x+a)=A cos w x+B sin w x]
के आरेख को ज्या तरंग (sine wave) कहते हैं, यहां पर तरंग का आवर्तांक (period of wave) २p/ओ (२p/w) है, म (M) आयाम (mplitude) का महत्तम मान और ऐ (a) कला (phase) है।
ज्या तरंग की आवश्यकता प्रत्यावर्ती विद्युतद्धारा (alternating electric current), प्रकाश, ध्वनि और उन आवर्त (periodic) घटनाओं का अध्ययन, जिनमें अधिस्वरक (overtone) की उपस्थिति के कारण स्वरक में शुद्धता की मात्रा कम है, निम्नलिखित त्रिकोणमितीय बहुपदीय फलन की सहायता से किया जाता है :
१/२ अ0 + अ१ कोज्या ओय + ब१ ज्या ओय + ............ +
अन कोज्या नओय + बन ज्या नओय।
[1/2 A0 + A1 cos w x + B1 sin w x + ........... +
An cos nwx + Bn sin nwx]
[विक्रमादिल्य राय]