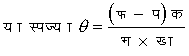
तुला वह यंत्र है जिसकी सहायता से दो वस्तुओं की संहतियों की तुलना की जाती है और किसी वस्तु की संहति या भार (weight), मानक संहतियों या बाटों के भार से तुलना के द्वारा, ज्ञात किया जाता है।
समभुज (equal arm) तुला का उपयोग मिस्र देशवासी प्राय: प्रागैतिहासिक युग से ही करते रहे हैं। मिस्र के कई सहस्र वर्ष प्राचीन भवनों के घ्वंसावशेषों की खुदाई के क्रम में पुरातत्ववेत्ताओं ने पत्थर से गढ़ी गई तुलाएँ प्राप्त की हैं, जिनके साथ पत्थर के ही अत्यंत कुशलतापूर्वक गढ़े गए बाट भी मिले हैं। ऐसी एक तुला का चित्र यहाँ दिया जा रहा है (चित्र १)। इसकी डंडी और बाट चूना पत्थरों के बने हुए हैं।
चित्र १. प्रागैतिहासिक मिस्री तुला
नकदा (मिस्र) से प्राप्त ७,००० वर्ष प्राचीन तुला। क, ख, ग और घर विभिन्न बाट तथा च तुला का दंड। ये सब पत्थर के हैं।
लंदन के विज्ञान संग्रहालय में ऐसी ही एक तुला रखी हुई है। अनुमान है कि ऐसी तुला का उपयोग प्राय: ५,००० ईo पूo तक होता रहा है। ऐसा विश्वास है कि इन तुलाओं का उपयोग स्वर्णधूलि को तौलकर, उसमें विद्यमान स्वर्णांश का आकलन करने के हेतु किया जाता था। आदिम तुला में एक लंबी डंडी होती थी, जिसके दोनों सिरों के समीप, डंडी की लंबाई के लंबवत्, छिद्र होते थे। इनमें से तागा या सुतली लटकाई जाती थी और उनके निचले सिरों से दो पलड़े लटके रहते थे, जिनपर तौली जानेवाली वस्तु एवं बाट रखे जाते थे। इस डंडी को बीच में एक आलंब से लटकाया जाता था। चित्र २. में प्रदर्शित तुला का प्रयोग आज से प्राय: ३,५०० वर्ष पूर्व मिस्र देश में किया जाता था। आधुनिक तुला का यह संभवत: आदिम रूप था। इस तुला को डंडी और पलड़े लकड़ी के और बाट काँसे (bronze) के होते थे। इस तुला से लगभग एक किलोग्राम का भार साधा जा सकता था और एक ग्राम के बराबर भारांतर ज्ञात किया जा सकता था। कालांतर में, आज से प्राय: २,००० वर्ष पहले, डंडी की ठीक क्षैतिज स्थिति देखने के लिये डंडी के मध्य बिंदु से एक सूई लटकाने का प्रयोग रोमन लोगों द्वारा आरंभ किया गया। यह सूई जब ठीक ऊर्ध्वाधर होती थी तो डंडी पूर्ण क्षैतिज मानी जाती थी। इसके बाद सुधारों के क्रम में क्षुरधारों (knife edges) का आविष्कार हुआ। इनके प्रयोग ने आधुनिक सूक्ष्ममापी एवं सटीक तुलाओं को जन्म दिया।
चित्र २. प्राचीन मिस्री तुला
३,५०० वर्ष पूर्व की यह मिस्री तुला लकड़ी की है तथा विभिन्न आकृतियों के इसके बाट काँसे के हैं।
तुला का सिद्धांत -- तुला की रचना उत्तोलक (lever) के सिद्धांत पर की गई है। यह प्रथम कोटि के उत्तोलक का व्यावहारिक रूप है। एक सुदृढ़ डंडी के एक सिरे पर बोझ लटकाया जाता है और दूसरे सिरे पर उसे संतुलित करने के लिये वांछित भार लटकाया जाता है, जो शक्ति (effort or power) का रूप होता है। बीच में आलंब (fulcrum) पर यह डंडी संतुलित की जाती है। डंडी की क्षैतिज स्थिति में, आलंब के दोनों ओर कार्य कर रहे बलों के घूर्णों का ज्यामितीय योग शून्य के बराबर होता है। व्यावहारिक तुला में डंडी के दोनों सिरों से दो पलड़े लटकाए जाते हैं, जिनमें क्रमश: वस्तु और बाट रखे जाते हैं। यह डंडी बीच में एक क्षुरधार पर सधी रहती है, जिससे संपूर्ण तुला एक ऊर्ध्वाधर तल में घूर्णन कर सकती है।
भौतिक अथवा रासायनिक तुलाएँ अत्यंत सुग्राही होती हैं और उनमें पलड़ों को भी क्षुरधार पर ही सधा हुआ लटकाया जाता है। ऐसी एक तुला चित्र ३. में दिखलाई गई है। एक हलकी, किंतु दृढ़ धातु की डंडी में तीन क्षुरधार लगे हुए हैं। मध्य क्षुरधार उ की धार नीचे की ओर होती है, जो तुला के स्तंभ के सिर पर लगे हुए गोमेद की प्लेट पर टिका रहता है और तुला की साम्यावस्था में डंडी को साधे रहता है। शेष दोनों क्षुरधार डंडी के दोनों सिरों पर स्थित होते हैं। इनकी धारें ऊर्ध्वमुखी होती हैं और उनसे गोमेद के टुकड़ों के सहारे पलड़े लटके होते हैं। तुला की डंडी की स्थिति का निर्धारण धातु के एक लंबे संकेतक स द्वारा किया जाता है, जो नीचे लगे एक पैमाने प पर घूमता है और डंडी की संतुलित स्थिति में, या तो इस पैमाने के शून्य पर रहता है, अथवा उसके इधर उधर समान दूरी तक दोलन करता है। डंडी के अंतिम सिरों पर दो सूक्ष्म समंजक पेंच, स१ और स२, लगे होते हैं, जिनकी सहायता से डंडी को उस दशा में संतुलित करते हैं, जब कि दोनों पलड़ों में कोई भार नहीं रखा जाता।
संपूर्ण व्यवस्था को एक प्रकोष्ठ, या केस (case), में बंद कर दिया जाता है, जिसकी दीवारें काच की होती हैं। इससे तुला को बाहर से देखा जा सकता है। इस केस के आधार से एक उत्तोलक व्यवस्था का संबंध स्तंभ के अंदर ही अंदर आलंब से होता है। नीचे लगे हुए पेंच या हत्थे को घुमाने से डंडी स्वतंत्र रूप से ऊपर उठ जाती है, जिससे उसके संतुलित या असंतुलित होने का ज्ञान होता है।
चित्र ३. भौतिक तुला
उ. मध्य क्षुर धार; स. सूचक सूई; प. मापनी तथा स१ और स२ पेंच पर आगे पीछे हटनेवाले छोटे पिंड।
भौतिक तुला भौतिक तुला से प्राय: १ मिलिग्राम या .००१ ग्राम तक ठीक ठीक तोला जा सकता है। अत्यधिक सुग्राही विश्लेषक तुला में .०००१ ग्राम तक, या इससे भी अधिक सूक्ष्म भार, डंडी में बने हुए खाँचो में एक अत्यंत हलके तार के टुकड़े को लटका कर, ज्ञात किया जाता है। इस तार के टुकड़े को आरोही (Rider) कहते हैं।
प्रत्येक अच्छी तुला में निम्नलिखित विशेषताएँ होनी चाहिए:
(१) तुला सत्य हो अर्थात् डंडी की क्षैतिज स्थिति में उसके एक पलड़े पर रखी हुई वस्तु का भार उन बाटों के भार के ठीक ठीक बराबर हो जो दूसरे पलड़े पर रखे हुए हों, अथवा दोनों पलड़ों पर समान भार रखने पर डंडी क्षैतिज रहे।
(२) तुला सुग्राही हो, अर्थात् दोनों पलड़ों पर रखे हुए भारों में रंच मात्र अंतर भी वह स्पष्ट रूप से व्यक्त कर सके।
(३) तुला स्थिर हो, अर्थात् तौलते समय उसक डंडी बहुत अधिक ऊपर नीचे दोलन न करे, वरन् शीघ्र ही स्थिर हो जाय और (४) तुला दृढ़ हो, अर्थात् पलड़ों पर भार रखने पर उसकी डंडी अथवा पलड़े लचक न जाएँ।
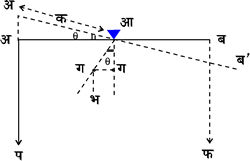
मान लिया पलड़ों पर क्रमश: प और फ (असमान) भार रखे हुए हैं (देखे चित्र ४.), जिससे डंडी क्षैतिज स्थिति अब से कोण बनाती हुई अ'ब' स्थिति में संतुलित होती है; फलस्वरूप तुला का गुरुत्वकेंद्र ग से हटकर ग' स्थिति में आ गया। मान लिया डंडी की आधी लंबाई क तथा आलंब आ से गुरुत्व केंद्र ग की दूरी ख है। अत: घूर्ण के नियम के अनुसार संतुलन की स्थिति में आलंब के दोनों ओर के बलों के घूर्ण के परस्पर बराबर होंगे। अर्थात्
प ´ अ आ + भ ´ ग ग' = फ ´ आ ब, जहाँ भ तुला का भार है।
अर्थात् प ´ क कोज्या q + भ ´ ख ज्या q = फ ´ क कोज्या q
अर्थात् भ ´ ख ज्या q = (फ - प) क कोज्या q
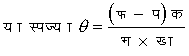
तुला की सुग्राहिता के लिये, q का मान अधिक होना चाहिए, अर्थात् स्पज्या q का मान अधिक होना चाहिए। अतएव
(१) क का मान अधिक होना चाहिए, अर्थात् तुला की डंडी लंबी होनी चाहिए।
(२) भ और ख के मान कम से कम हों, अर्थात् तुला हलकी होनी चाहिए और उसका गुरुत्वकेंद्र आलंब के सन्निकट स्थित होना चाहिए।
किंतु तुला के स्थायी होने के लिये डंडी को भारी होना चाहिए और इसका गुरुत्वकेंद्र आलंब से काफी नीचे स्थित होना चाहिए। अतएव तुला की सुग्राहिता और स्थायित्व की अर्हताएँ परस्पर विपरीत हैं। इससे स्पष्ट है कि कोई तुला परम सुग्राही और स्थिर, दोनों नहीं हो सकती।
अशुद्ध तुला से ठीक ठीक तौलना -- अशुद्ध तुला से किसी वस्तु का ठीक ठीक भार ज्ञात करने की निम्नलिखित दो विधियाँ हैं :
(१) बोर्डा की विधि -- तुला के दाहिने पलड़े पर वह वस्तु रखी जाती है जिसको तौलना है और बाएँ पलड़े पर रेत, मिट्टी या ऐसा ही कोई अन्य पदार्थ इतना रखा जाता है कि डंडी क्षैतिज हो जाय। फिर उस वस्तु को उतार कर उस पलड़े पर इतना बाट रखा जाता है कि डंडी पुन: क्षैतिज हो जाय। इस प्रकार रखे गए बाट का भार उस वस्तु के भार के समान होगा।
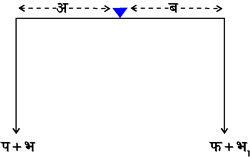
(२) गॉस की दोहरी तौल (Double Weighing) विधि -- मान लिया जिस वस्तु को तोलना है उसका वास्तविक भार भ ग्राम है। उसे ऐसी तुला से तौला जाना है जिसकी डंडी की लंबाई आलंब के दोनों ओर बराबर नहीं है और पलड़े भी असमान भार (प और फ ग्राम क्रमश:) के हैं। वस्तु को पहले एक पलड़े पर रखकर दूसरे पलड़े पर इतना बाट रखते हैं कि डंडी क्षैतिज हो जाय। इस स्थिति में मान लिया भ१ ग्राम भार के बाट रखने पड़े। तो घूर्ण के नियम (Law of moments) के अनुसार (देखें चित्र ५.) चित्र ५
 |
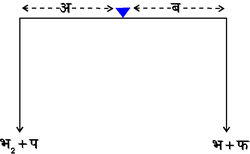 |
(प + भ) ´ अ = (फ + भ१) ´ ब१ अर्थात् भ ´ अ = भ१ ´ ब, क्योंकि प ´ अ = फ ´ ब (कोई भार न रहने पर डंडी क्षैतिज रहने के कारण)। अब वस्तु को दूसरे पलड़े पर रखते हैं और पहले पलड़े पर इतने भार (भ२ ग्राम) के बाट रखते हैं कि डंडी पुन: क्षैतिज हो जाय; तो पूर्वोक्त विधि से (भ२ + प) अ = (भ + फ) ब, किंतु प अ = फ ब, इसलिये भ२ अ = भ ब (देखें चित्र ६.)। चित्र ६
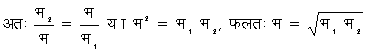
अर्थात् सही भार दोनों भारों के गुणनफल के वर्गमूल, या ज्यामितीय मध्यमान (geometrical mean) के बराबर होगा।
आलंब के दोनों ओर डंडी की लंबाइयों का अनुपात
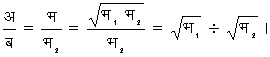
कमानीदार तुला (Spring Balance) -- उपर्युक्त तुला में वस्तु की संहति अन्य ज्ञात संहति की तुलना द्वारा ज्ञात की जाती है, किंतु कमानीदार तुला में वस्तु की संहति, या भार, पृथ्वी के गुरुत्वाकर्षण के प्रत्यक्ष प्रभाव के द्वारा ज्ञात किया जाता है। इसमें एक धात्विक ढाँचा होता है, जिसके अंदर एक सर्पिल कमानी होती है। कमानी का एक सिरा ढाँचे के सिरे पर जड़ा रहता है और दूसरा सिरा मुक्त रहता है। मुक्त सिरे से एक हुक (hook) लटका रहता है, जिससे तुलनीय वस्तु को फँसाकर लटकाया जाता है। इस प्रकार लटकी हुई वस्तु गुरुत्वाकर्षण के प्रभाव (या अपने भार) से नीचे की ओर खिंचती है, जिससे कमानी में भी अनुदैर्ध्य प्रसार होता है। कमानी से एक संकेतक (pointer) लगा होता है, जो तुला के ढाँचे पर अंशांकित पैमाने पर ऊपर से नीचे की ओर चलता है। यह पैमाना ग्राम या पाउंड में मपा हुआ रहता है। संकेतक जिस स्थान पर जाकर रुक जाता है, वहाँ पैमाने का पाठ्यांक पढ़ लिया जाता है। यही पाठ्यांक उस वस्तु की संहति व्यक्त करता है और उसमें गुरुत्व ग (g) का गुणा कर देने पर वस्तु का भार ज्ञात हो जाता है।

चित्र ७. कमानीदार तुला
सूक्ष्ममापी तुला (Microbalance) -- अत्यंत सूक्ष्म भौतिक एवं रासायनिक संहतियों को मापने के लिये सूक्ष्ममापी तुला, या माइक्रोतुला, का प्रयोग किया जाता है। गैसों का घनत्व, विशेषकर अत्यल्प मात्रा में उपलब्ध गैसों का घनत्व, ज्ञात करने के लिये इस प्रकार की तुलाएँ अधिक उपयोगी होती हैं। इस तुला के क्षुरधार स्फटिक या क्वार्ट्ज के बने होते हैं। इनमें भारांतर ज्ञात करने के लिये बाटों के बदले गैस के उत्ल्पावन बल का उपयोग किया जाता है। इस बल की माप गैस की दाब के द्वारा की जाती है। इस दाब को प्रयोजन के अनुसार नियंत्रित किया जा सकता है। इन कारणों से इन तुलाओं को गैस प्रकोष्ठों में परिचालित किया जाता है। इन प्रकोष्ठों से पारद वायुदाबमापी संबंधित रहते हैं, जो गैस की दाब व्यक्त करते हैं। ऐसी एक तुला का चित्र यहाँ दिया गया है (देखें चित्र ८.)।
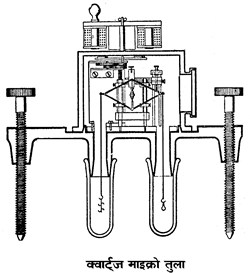
चित्र ८. क्वार्ट्ज़ माइक्रो तुला
माइक्रोतुला से भी अधिक सूक्ष्म परिमाणों की व्यक्त करने के लिये अति सूक्ष्म अथवा अल्ट्रामाइक्रो तुलाओं का उपयोग किया जाता है। यह तुला ५ ´ १०-८ ग्राम तक ठीक ठीक माप सकती है। सामान्य तुला की ही भाँति इस तुला की डंडी भी बीच में अवलंबित रहती है और प्रत्येक सिरे से एक हलका पलड़ा लटका रहता है। डंडी स्वयं भी हलके स्फटिक की बनी होती है और स्फटिक के ही लंबे तंतुओं पर टिकी हुई होती है। इसकी कार्यप्रणाली सूक्ष्ममापी तुला की ही भाँति होती है।
सामान्य रोमन विषमभुज तुला (Roman Steel Yard) -- यह तुला भी प्रथम श्रेणी के उत्तोलक के सिद्धांत पर निर्मित की जाती है। इसकी एक भुजा बहुत छोटी और दूसरी बहुत बड़ी होती है। आलंब अ के बाईं ओर छोटी भुजा से वह भार भ लटकाया जाता है, जिसे तौलना होता है, और दाहिनी ओर बड़ी भुजा से जिसमें समान दूरियों पर पैमाने के चिह्न कटे होते हैं, एक निश्चित बाट व आलंब से इतनी दूरी पर लटकाया जाता है कि वह भार भ को साध ले। जब डंडी क्षैतिज रहती है, तो भ और ब के आलंब के चारों ओर घूर्णां परस्पर बराबर होंगे। पहले विभिन्न ज्ञात भारों को भ के स्थान पर लटका कर ब द्वारा साधा जाता है, इससे यह ज्ञात हो जाता है कि पैमाने के किस पाठ्यांक पर ब कितने भार को साध लेता है। इस प्रकार तुला का मानकीकरण करके किसी भी अज्ञात भार का मान ज्ञात किया जा सकता है। इसमें सुविधा यह है कि एक ही बाट द्वारा किसी भी भार का मान ज्ञात किया जा सकता है।
चित्र ९. रोमन विषमभुज तुला
अ आलंब, ब. बल का कार्य करनेवाला बाट तथा भ. भार।
मंचतुला (Platform Balance) -- बहुत बड़े भार को साधारण तुला द्वारा नहीं तौला जा सकता, क्योंकि तुला की डंडी तथा पलड़ों की दृढ़ता सीमित होती है। इस हेतु एक विशेष प्रकार की तुला का निर्माण किया गया है, जिसे मंचतुला कहते हैं। इस तुला में तीन उत्तोलक होते हैं, जो क्रमश: तीन आलंब आ१, आ२ और आ३ पर टिके होते हैं। मंच अब दो क्षुर धारों क्ष१ और क्ष२ पर टिका होता है, जो क्रमश: आलंब आ१ और आ२ के समीप होते हैं। मंच पर जब कोई भार रखा जाता है तो उसका दाब क्ष१ और क्ष२ क्षुरधारों पर पड़ता है, जिससे आ१ पर टिके हुए आलंब का क सिर नीचे दबता है और आ३ आलंब के सिरे ख को भी नीचे खींचता है।
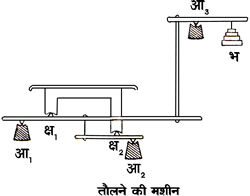
चित्र १०. तौलने की मशीन
आ१, आ२ तथा आ३ विविध आलंब क्ष१ तथा क्ष२ क्षुरधाराएँ तथा भ भार।
इसे पुन: क्षैतिज करने के लिये भार भ को आलंब से दूर हटाते हैं और ऊपर वर्णित विधि से मंच पर रखी हुई वस्तु का भार कर लेते हैं। [सुरेशचंद्र गौड़]