तरंगगति जल के पृष्ठ पर उत्पन्न होनेवाली तरंगों या लहरों से सभी परिचित हैं। जल के शांत समतल पृष्ठ के किसी बिंदु को थोड़ा सा विस्थापित कर देने पर जलपृष्ठ की आकृति वक्र रूप की हो जाती है। कहीं कहीं जल ऊँचा उठा हुआ दिखाई देता है और इन उठे हुए स्थानों के बीच बीच में जल नीचे धँसा हुआ होता है। इस वक्र आकृति को ही तरंग कहते हैं और उसके ऊँचे भाग को शीर्ष तथा नीचे भाग को गर्त कहते हैं। किसी भी शीर्ष या गर्त पर दृष्टि जमाने से वह तथा शीर्ष गर्तमय वक्र आकृति जलपृष्ठ पर नियत वेग से स्थानांतरित होती हुई दिखाई देती है।
ऐसे तरंगित जल पर एक तिनका डाल देने से दो मुख्य बातें प्रकट होती हैं। तिनका बारंबार ऊपर और नीचे गिरता है, किंतु अपने स्थान से हटकर तरंग के साथ अन्यत्र नहीं चला जाता। इसका स्पष्ट अर्थं है कि जल का प्रत्येक कण ऊपर नीचे की दिशा में दोलन करता है, किन्तु वह उस दिशा में स्थानांतरित नहीं होता जिसमें तरंग चलती है। जो चीज स्थानांतरित होती है वह है जलपृष्ठ का विकृत रूप और उस विकृति को उत्पन्न करनेवाली होती है ऊर्जा।
जल के अतिरिक्त अन्य पदार्थो में, लोआ, पीतल, वायु आदि, में भी इसी प्रकार की तरंगे उत्पन्न होती हैं, किंतु बहुधा हम इन्हें प्रत्यक्षत: देख नहीं सकते। इन सब में भी कोई द्रव्यकण स्थानांतरित नहीं होता, किंतु ऊर्जा उत्तरोत्तर एक कण से दूसरे कण में होती हुई बड़े वेग से स्थानांतरित होती है। वायु में ध्वनि की ऊर्जा इसी प्रकार गमन करती है। अत: ध्वनिविज्ञान में तरंगगति का बहुत महत्व है। प्रकाश तथा रेडियो के संचरण को समझने के लिए तरंगगति का अध्ययन आवश्यक है।
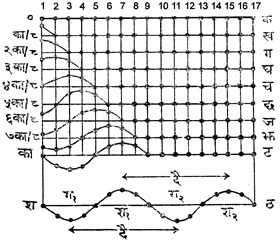
तरंग कैसी बनती है-- मान लीजिए कुछ द्रव्यकण बराबर बराबर दूरी पर सीधी पंक्ति में अवस्थित हैं (देखें चित्र १ में क) और पंक्ति में प्रत्यास्थता (इसपर लेख देखें) का गुण है, अर्थात बाह्यबल द्वारा इस पंक्ति में किसी प्रकार की विकृति हो जाने पर उसमें एक आंतरिक बल प्रकट हो जाता है, जो उस विकृति को मिटाने का प्रयत्न करता है। लंबी रस्सी ऐसी पंक्ति का अच्छा उदाहरण है।
अब मान लिजिए कि कण १ को हम थोड़ा सा ऊपर की ओर विस्थापित कर के छोड़ देते हैं। परिणाम यह होगा कि थोड़ी देर बाद कण २ भी उसी दिशा में स्वयमेव विस्थापित हो जायेगा। इसी प्रकार उत्तरोत्तर अन्य कण भी विस्थापित हो जाएँगे। इसी बीच में कण १ अपने पूर्व स्थान पर लौटने का प्रयत्न करेगा और घड़ी के लोलक

के समान
यह ऊपर नीचे
दोलन करने
लगेगा। मान लीजिए
इस दोलन का आवर्तकाल
का (T)
सेकंड है। फलत:
अन्य कण भी उसी प्रकार
से दोलन करने
लगेंगे, किंतु प्रत्येक
कण का दोलन
पूर्ववर्ती कण
के दोलन से कुछ
देर बाद प्रारंभ
होगा। अत: प्रत्येक
कण की कला पूर्ववर्ती
कण की कला से
कुछ पिछड़ी हुई
रहेगी और
किसी भी क्षण पर
समस्त कणों के
विस्थापन भिन्न
भिन्न मानों के
होंगे। फलत: कणपंक्ति
वक्र रूप प्राप्त कर
लेगी। चित्र १. में
इस पंक्ति की ![]() सेकंड के अंतराल
से उत्तरोत्तर
होनेवाली विभिन्न
आकृतियाँ दिखाई
गई है चित्र (ग)
कण १ का विस्थापन
महत्तम हो गया
है और इसके
बाद के चित्रों
में क्रमश: कण २, ३, ४ आदि
महत्तम विस्थापन
प्राप्त करते हैं।
चित्र (ट) में का (T)
सेकंड के बाद
की स्थिति प्रदर्शित
है जब कण १ पूरा
एक दोलन समाप्त
कर चुका है। चित्र
(ठ) में २का (२T)
सेकंड के बाद
की स्थिति दिखाई
गई है। जब तक
कण १ दोलन करता
रहेगा तब तक
वहाँ नए शीर्षों
और गर्तों का
निर्माण होता
रहेगा और
प्रत्येक शीर्ष या
गर्त कणपंक्ति
में दाहिनी ओर
अग्रसर होता रहेगा।
सेकंड के अंतराल
से उत्तरोत्तर
होनेवाली विभिन्न
आकृतियाँ दिखाई
गई है चित्र (ग)
कण १ का विस्थापन
महत्तम हो गया
है और इसके
बाद के चित्रों
में क्रमश: कण २, ३, ४ आदि
महत्तम विस्थापन
प्राप्त करते हैं।
चित्र (ट) में का (T)
सेकंड के बाद
की स्थिति प्रदर्शित
है जब कण १ पूरा
एक दोलन समाप्त
कर चुका है। चित्र
(ठ) में २का (२T)
सेकंड के बाद
की स्थिति दिखाई
गई है। जब तक
कण १ दोलन करता
रहेगा तब तक
वहाँ नए शीर्षों
और गर्तों का
निर्माण होता
रहेगा और
प्रत्येक शीर्ष या
गर्त कणपंक्ति
में दाहिनी ओर
अग्रसर होता रहेगा।
तरंगदैर्ध्य - चित्र (ठ) में एक शीर्ष से दूसरे शीर्ष तक की दूरी श१ श२ अथवा एक गर्त से दूसरे गर्त की दूरी ग१ ग२ तरंग की लंबाई या तरंगदैर्ध्य दै (l ) कहलाती है। यह भी स्पष्ट है कि दूरी पर अवस्थित कोई भी दो कण सदा समान कला में रहेंगे।
तरंग का वेग - इन चित्रों से यह भी स्पष्ट है कि जितने समय में कण एक दोलन पूरा कर लेता है (अर्थात का सेकंड में) उतने समय में तरंग पूरे एक तरंगदैर्ध्य की दूरी तय कर लेती है अत: उसका वेग वे = दै/का (l /T) होगा। प्रत्येक कण के एक सेकंड में होनेवाले दोलनों की संख्या को आवृति आ (n) कहते है। स्पष्ट है कि आ = १/का (n=१/T)
अत:, वे = आ दै (v=nl )........................(१)
कलांतर - दै (l ) की दूरीवाले कण समान कलाओं में रहते हैं। अत: उनका कलांतर २p रेडियन होता है। दै/२(l /२) की दूरी वाले कण विपरीत कलाओं में रहते हैं। उनका कलांतर p होता है। जिन कणों की दूरी य(x) है, स्पष्टत: उनका कलांतर होगा २p य/दै (२p x/l )। कलांतर तथा तरंगदैर्ध्य के इस नियत संबंध के कारण यह कलांतर कोण के स्थान में तरंगदैर्ध्य के द्वारा भी व्यक्त किया जाता है। इस दृष्टि से २p के कलांतर को दै (l ) का कलांतर, p को दै/२ (l /२) का और २p य/दै (२p x/l ) को य/दै (x/l ) का कलांतर भी कहते हैं।
तरंग
का गतिसमीकरण
- यदि प्रथम कण
के दोलन का
गतिसमीकरण
वि = म
ज्या २p आस ![]() हो, तो इससे
य (x)
की दूरीवाले
कण का गतिसमीकरण
होगा वि=मज्या
२p (आ स- य/दै)
हो, तो इससे
य (x)
की दूरीवाले
कण का गतिसमीकरण
होगा वि=मज्या
२p (आ स- य/दै)![]() यहाँ वि (S)
कण का विस्थापन
है और म (a)
उसका आयाम।
यहाँ वि (S)
कण का विस्थापन
है और म (a)
उसका आयाम।
म दै = दै/का = वे (nl =l /T=v) होने के कारण इस समीकरण के अन्य रूप है:
![]()
![]() (२)
(२)
यह ही सरल आवर्त तरंग के समीकरण हैं। म (a) ही तरंग का आयाम कहलाता है। ऊपर तरंग के जो लक्षण बताए गए हैं वे सब इस समीकरण से प्राप्त हो सकते हैं। इसमें स (t) की अपेक्षा भी आवर्तत्व है और य (x) की अपेक्षा भी। य (x) नियत कर देने पर, यह उस स्थान के कण के दोलन को व्यक्त करता है। स (t) को नियत कर देने पर यह एक क्षणविशेष पर कणपंक्ति की वक्र आकृति को व्यक्त करता है। यह (x) के मान में दै (l ), २ दै (२l ) आदि की वृद्धि करने पर विस्थापन अपरिवर्तित रहता है, अर्थात दै, २ दै आदि दूरीवाले कण समान कला में रहते हैं।
इस समीकरण का अधिक व्यापक रूप वह है जो इसे दो बार अवकलित करने पर प्राप्त होता है और वह है
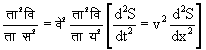 ............ २(क)
............ २(क)
यदि तरंग बाई ओर, अर्थात् य (x) ऋण दिशा में चले, तो उसका समीकरण होगा:
![]()
कर्णविस्थापन वि (S) तरंगगति की दिशा य (x) से समकोणिक होने के कारण, यह तरंग अनुप्रस्थ कहलाती है। यह केवल ठोस और द्रव पदार्थो में ही हो सकती है, जिनकी प्रत्यास्थता आकृति के परिवर्तन का विरोध कर सकती है। गैसों में ऐसी प्रत्यास्थता नहीं होती। अत: उनमें अनुप्रस्थ तरंगों का अस्तित्व संभव नहीं है।
अनुर्दर्ध्य तरंग - यदि चित्र १. की कणपक्ति से कणों का विस्थापन वि (S) पंक्ति की दिशा य (x) में ही हो, तो इस पंक्ति की उत्तरोत्तर होनेवाली अवस्थाएँ चित्र २. में दिखाई गई हैं। पंक्ति तो सीधी ही बनी रहती है, किंतु कणों की पारस्परिक दूरियाँ बदल जाती हैं। कहीं तो कण पास पास आ जाते हैं और कहीं दूर दूर हो जाते हैं, अर्थात् कहीं उनका घनत्व बढ़ जाता है और कहीं घट जाता है।
चित्र २
महत्तम घनत्व की अवस्था को संघनन तथा न्यूनतम घनत्व की अवस्था को विरलन कहते हैं, और ये एंकातरत: अवस्थित होकर पंक्ति की दिशा में नियत वेग से स्थानांतरित होते जाते हैं। दो निकटतम संघननों की, अथवा दो निकटतम विरलनों की, दूरी एक तरंगदैर्घ्य कहलाती है। इस प्रकार की तरंग को अनुदैर्घ्य तरंग कहते हैं। वायु में तथा अन्य गैसों व केवल ऐसी ही तरंगे पैदा हो सकती हैं, किंतु द्रवों में तथा ठोस पदार्थों में अनुप्रस्थ तथा अनुदैर्घ्य दोनों ही प्रकार की तरंगें उत्पन्न हो सकती हैं।
यदि तरंग समीकरण (२) तथा (२ क) में वि (S) की दिशा कही समझ ली जाय जो य (x) की है, तो ये ही समीकरण अनुदैर्घ्य तरंग को भी व्यक्त कर सकते हैं। चित्र १. तथा २ की तुलना से प्रकट होता है कि संघनन या विरलन उन स्थानों पर नहीं हैं जहाँ अनुप्रस्थ तरंग में शीर्ष या गर्त होते हैं, अर्थात् जहाँ कणविस्थापन अधिकतम होता है। ये उन स्थानों पर होते हैं जहाँ कणवेग अधिकतम होता है।
माध्यम
और तरंगवेग
- तरंग का वेग
उस पदार्थ के गुणों
पर अवलंबित है,
जिसमें तरंग
चलती है और
जिसे माध्यम कहते
हैं। ये गुण हैं:
(१) प्रत्यास्थता तथा
(2)
अवस्थितित्व। विभिन्न
अवस्थाओं में तथा
विभिन्न प्रकार
की तरंगों में
प्रभावक प्रत्यास्थता
भी विभिन्न प्रकार
की होती है और
अवस्थितित्व भी विभिन्न
रूपों में प्रकट
होता है। किंतु
यदि इनके यथोचित
मानों का उपयोग
किया जाय तो
यह प्रमाणित किया
जा सकता है कि
तरंग का वेग
![]() , जहाँ
प्र (E)
उपयुक्त प्रत्यास्थता
का मान है और
सं (K)
अवस्थितित्व पर
आश्रित संख्या है।
वायु आदि गैसों
में इस सूत्र का
रूप हो जाता है:
, जहाँ
प्र (E)
उपयुक्त प्रत्यास्थता
का मान है और
सं (K)
अवस्थितित्व पर
आश्रित संख्या है।
वायु आदि गैसों
में इस सूत्र का
रूप हो जाता है:
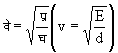
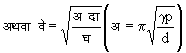
यहाँ प्र (E) तो आयतन प्रत्यास्थता है, जिसका मान समतापीय अवस्था में गैस के दबाव दा (P) के बराबर होता है और रुद्धोष्म अवस्था में अ दा (g P) के बराबर होता है, जहाँ अ (g )
![]() तथा घ (d)
गैस का घनत्व है,
तथा घ (d)
गैस का घनत्व है,
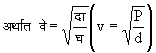
 ।
।
इस अंतिम
सूत्र के अनुसार
वायु में ध्वनि
की तरंगों का
वेग प्राप्त होता
है और लगभग
३३२ मीटर प्रति सेकंड
होता है। लंबे
तार में चलनेवाली
अनुप्रस्थ तरंग का
वेग होता है
![]() , जहाँ
त (T)
तो तार का तनाव
है और द्र (m)
तार की एक सेंटीमीटर
लंबाई का द्रव्यमान।
, जहाँ
त (T)
तो तार का तनाव
है और द्र (m)
तार की एक सेंटीमीटर
लंबाई का द्रव्यमान।
तरंगों का संयोजन - जब एक ही माध्यम में दो तरंगें एक साथ चल रही हों तब उसके प्रत्येक कण में दोनों तरंगें अपने अपने दोलन उत्पन्न करने का प्रयत्न करेंगी। फलत: जो दोलन उत्पन्न होगा वह दोनों दोलनों के संयोजन का परिणाम होगा। यदि दोनों तरंगों के विस्थापन एक ही दिशा में हों, तो प्रत्येक क्षण पर परिणामी विस्थापन दोनों संघटक विस्थापनों के बीजीय योग के बराबर होगा और स्पष्टत: इसका मान दोनों तरंगों के कलांतर पर अवलंबित होगा। यदि यह कलांतर ० या २ होगा तब तो यह दोनों तरंगों के आयामों के जोड़ के बराबर होगा। यदि कलांतर या ३ हो तो यह उन आयामों के अंतर के बराबर होगा और यदि दोनों आयाम बराबर हों तो परिणामी आयाम शून्य हो जायेगा, अर्थात इस दशा में विपरीत कला वाली तरंगें एक दूसरी को सर्वथा नष्ट कर देंगी। बीजगणित द्वारा ये बातें स्पष्ट हो जाती हैं।
यदि संघटक तरंगों के समीकरण
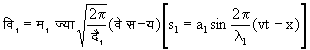
तथा 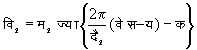
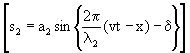
हों, जहाँ (d ) कलांतर को व्यक्त करता है, तो परिणामी तरंग का समीकरण होगा
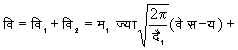

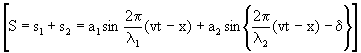
और यदि ![]() हो तो यह समीकरण हो जायगा:
हो तो यह समीकरण हो जायगा:
![]()
![]()
जहाँ ![]() तथा स्पर्शज्या को
तथा स्पर्शज्या को
![]()
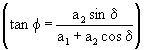
स्पष्टत: ![]() , जब
, जब ![]() तथा
तथा ![]() , जब
, जब ![]() ।
।
तरंग की आकृति - यद्यपि बराबर आवृत्तिवाली सरल आवर्त तरंगों के संयोजन से जो परिणामी तरंग प्राप्त होती है वह भी सरल आवर्त होती है, तथापि विभिन्न आवृत्तियोंवाली तरंगों से प्राप्त परिणामी
चित्र ३
तरंग सरल आवर्त नहीं होती। ऐसी तरंग के समीकरण का व्यापक रूप है वि = फ (वे स - य) (S=f(vt -x))। इसका भी अवकल रूप समीकरण (२ क.) ही है। उसका विस्थापनवक्र ज्यावक्र नहीं होता। उसकी आकृति अन्य प्रकार की होती है। इस आकृति को ही तरंग की आकृति कहते हैं। दो से अधिक तरंगों के संयोजन से प्राप्त आकृति और भी जटिल होती है।
किंतु फूरियर
के प्रमेय के द्वारा
किसी भी आकृति
की तरंग का विश्लेषण
करके उसकी संघटक
सरल आवर्त तरंगों
का पता लगाया
जा सकता है। यदि
उस तरंग का तरंगदैर्ध्य
दै (l ) हो
तो इन संघटक
तरंगों के तरंगदैर्घ्य
क्रमश: ![]() आदि होते हैं।
आदि होते हैं।
अप्रगामी तरंग - यदि बराबर आयामों तथा आवृत्तियोंवाली दो तरंगें विपरीत दिशाओं में चल रही हों, पतली रेखाएँ संघटक तरंगों को तथा मोटी रेखा परिणामी तरंग को व्यक्त करती है। विभिन्न समयों के चित्र अलग अलग दिए गए हैं। इनसे प्रकट होता है कि
अनुदैर्ध्य तरंगों के द्वारा भी अप्रगामी तरंगें बनती हैं। इनमें भी कुछ कणों का विस्थापन महत्तम होता है और कुछ कण अपने स्थान पर अचलन रहते हैं। ये ही प्रस्पंदों तथा निष्पंदों के स्थान हैं। इनमें कणों की पारम्परिक दूरियों में परिवर्तन होता है, जिसे हम घनत्व का परिवर्तन कह सकते हैं। यह घनत्व परिवर्तन निष्पंदों पर महत्तम होता हैं। वहाँ कभी तो घनत्व बहुत बढ़ जाता है और अर्ध आवर्तकाल के बाद बहुत घट जाता है।
तरंग का परावर्तन - जब कोई तरंग माध्यम के सीमांत पर पहुँच जाती है औरा वहाँ किसी दूसरे माध्यम का प्रारंभ होता है, तब इस सीमांत से एक तरंग विपरीत दिशा में चलने लगती है। इस घटना को तरंग का परावर्तन कहते हैं और यह नई तरंग परावर्तित तरंग कहलाती है।
जब दूसरा माध्यम प्रथम की अपेक्षा अधिक भारी, या सर्वथा अचल, होता है तब तो इस सीमांत पर कर्ण विस्थापन घट जाता है, अर्थात् परावर्तित तरंग की कला आपतित तरंग की कला से विपरीत होती हैं, और जब दूसरा माध्यम हल्का होता है तब परावर्तित तरंग की कला समान होती है।
यदि आपतित तथा परावर्तित दोनों तरंगें माध्यम में चलती रहें तो परिणाम यह होता है कि अप्रगामी तरंग बन जाती है और माध्यम में प्रस्पंद तथा निष्पंद बन जाते हैं। जब तरंग अधिक भारी माध्यम से परावर्तित होती है तब तो सीमांत पर निष्पंद बनता है और यदि दूसरा माध्यम हलका हो तो वहाँ प्रस्पंद बन जाता है।
तरंगाग्र - अभी तक ऐसी तरंग पर विचार किया गया है जो केवल एक ही दिशा में गमन करती हैं, किंतु जल के विस्तृत पृष्ठ पर तरंगे उद्गम स्थान से चारों दिशाओं में समान वेग से फैलती हैं। अत: उनके शीर्ष तथा गर्त उद्गम स्थान के चारों ओर बराबर दूरी पर स्थित होते हैं और हमें वृत्ताकार दिखाई देते हैं। शीर्ष या गर्त के ऐसे वृत्तों को तरंगाग्र कहते हैं। व्यापकत: समान कला में विद्यमान कणों के बिंदुपथ का नाम तरंगाग्र है।
जब तरँग वायु अथवा अन्य द्रव्य के किसी अर्तरंग बिंदु से उत्पन्न होती है तब वह समस्त दिशाओं में समान वेग से फैलती है और उसके तरंगाग्र गोलाकार होते हैं। जब गोलाकार तरंग उग्दम स्थान से बहुत अधिक दूर (अनंत दूर) पहुँच जाती हैं तब इन तरंगाग्रों की त्रिज्या का मान भी बहुत बड़ा (अनंत) हो जाता है और किसी भी दिशा में तरंगाग्र समतल समझा जा सकता है। तब तरंग समतल तरंग कहलाती है।
वृत्तीय तथा गोलीय तरंगों के आयाम - एक ही दिशा में चलने वाली तरंग में समस्त कणों की ऊर्जा तथा उनके आयाम बराबर होते है। किंतु वृत्तीय अथवा गोलीय तरंगों में जो ऊर्जा उद्गम स्थान से स्थानांतरित होती है वह उत्तरोत्तर अधिक संख्यक कणों में वितरित हो जाती है। चित्र ४. में जो ऊर्जा ऊ (E) समय त्रिज्या = त्रि१ (r१) वाले वृत्त कखग पर थी वही थोड़ी देर बाद त्रिजया = त्रि२ (r२) वाले
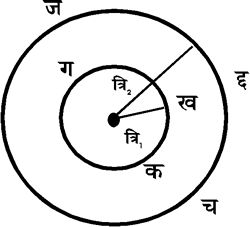
वृत्त चछज
पर पहुँच जाती
है। इन वृत्तों की
लंबाई क्रमश: २p
त्रि१(२p
r१)
तथा २p त्रि२(२p
r२)
है। अत: इनपर स्थित
कणों की संख्याएँ
भी २p त्रि१(२p
r१)
तथा २p त्रि२(२p
r२)
की अनुपाती होंगी।
फलत: इन वृत्तों
के प्रत्येक कण की
ऊर्जाओं का अनुपात
होगा 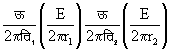 अर्थात्
अर्थात् 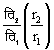 और उनके आयामों
का अनुपात होगा
और उनके आयामों
का अनुपात होगा
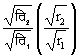 । अत: ऐसी
तरंग का समीकरण
यों लिखा जाएगा:
। अत: ऐसी
तरंग का समीकरण
यों लिखा जाएगा:
![]()
![]()
इसी प्रकार क ख ग तथा च छ ज गोलाकार हों तो उनपर स्थित कणों की संख्याएँ इन गोलाकार पृष्ठों के क्षेत्रफलों की अनुपाती होंगी, अर्थात् उनका अनुपात होगा ४p त्रि१२ : ४p त्रि२२ (४p r१२ : ४p r२२)। अत: उनकी ऊर्जाओं का अनुपात होगा
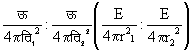 यह
व्युत्क्रम वर्ग नियम
कहलाता है। उनके
आयामों का अनुपात
होगा
यह
व्युत्क्रम वर्ग नियम
कहलाता है। उनके
आयामों का अनुपात
होगा 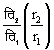 फलत: गोलीय
तरंग का समीकरण
होगा:
फलत: गोलीय
तरंग का समीकरण
होगा:
![]()
![]()
स्पष्ट है कि वृत्तीय गोलीय तरंगों के आयाम क्रमश: घटते जाते हैं। गोलीय तरंगों का अवकल समीकरण है:
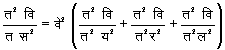
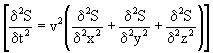
अद्रव्य तरंगें - यह नहीं समझना चाहिए कि द्रव्यकणों के विस्थापन के द्वारा ही तरंगें बन सकती हैं। किसी भी भौतिक राशि, यथा चुंबकीय बल अथवा वैद्युत बल, के मान में यदि समय की अपेक्षा तथा स्थान की अपेक्षा आवर्त परिवर्तन हों तो ये परिवर्तन भी समीकरण (२) तथा (२ क) द्वारा व्यक्त किए जा सकते हैं। अत: इस द्विविध आवर्तन को भी तरंग ही कहते हैं। चुबकीय तरंग वैद्युत तरंग, विद्युच्चुंबकीय तरंग ऐसी ही तरंगें हैं। प्रकाश तथा रेडियों विद्युच्चुंबकीय तरंगों के ही रूप हैं। द्रव्य की गति के आधुनिक सिद्धांत के अनुसार द्रव्य की गति भी ऐसी तरंगों का परिणाम है जिन्हें द्रव्य तरंगें कहते हैं। इन तरंगों के विज्ञान को तरंगयांत्रिकी नाम दिया गया है। [निहालकरण सेठी]