ज्यामिति गणित की वह शाखा है जिसमें बिंदुओं, रेखाओं, वक्रों, समतलों इत्यादि का अध्ययन होता है। भूमि के नाप संबंधी कार्यों से इन विज्ञान की उत्पत्ति हुई, इसलिये इस गणित को भूमिति भी कहते हैं। आरंभ में यह अध्ययन रेखाओं तथा रेखाओं से घिरे क्षेत्रों के गुणों तक ही सीमित रहा, जिसके कारण ज्यामिति का नाम रेखागणित भी है। भारत में यज्ञवेदियों के निर्माण कार्य में गणितज्ञों का ध्यान ज्यामिति के अध्ययन की और आकृष्ट किया, उनके अध्ययन में क्षेत्रसमिति का पुट अधिक था। इतिहासयज्ञों का मत है कि भारतवासी ईसा से १,००० वर्ष पूर्व ऐसे संबंध जैसे 32 + 42 = 52 (32 + 42 = 52) जानते थे, परंतु ऐसे ही कतिपय छुटपुट समीकरणों के अतिरिक्त उन्होंने ऐसे संबंधों का किसी व्यापक रूप से अध्ययन नहीं किया। ईसा से लगभग ६०० वर्ष पूर्व रोम के गणितज्ञ पिथागोरैस ने इस संबंध का बड़े तर्कपूर्ण ढंग से अध्ययन किया और यह बताया कि एक समकोण त्रिभुज में कर्ण पर का वर्ग अन्य भुजाओं के ऊपर वर्गों के योगफल के बराबर होता है।
वैसे तो ज्यामिति का अध्ययन सभी पुराने सभ्य देशों, जैसे मिस्र, बैबिलोनिया, चीन, भारत तथा यूनान, में लगभग साथ ही साथ आरंभ हुआ, परंतु जितनी उन्नति इस विज्ञान में यूनान ने की उतनी किसी और देश ने नहीं की। ईसा से लगभग ३०० वर्ष पूर्व यूनान के एक गणितज यूक्लिड ने उस समय तक जितने तथ्य ज्ञात थे उन सबको बड़े तर्कपूर्ण ढंग से क्रमबद्ध किया। ज्ञात तथ्यों के आधार पर उसने अन्य तथ्य सिद्ध करने का प्रयत्न किया। इस प्रकार तथ्यों को क्रमबद्ध करने पर वह कुछ ऐसे प्रारंभिक तथ्यों पर पहुँचा जिनको सिद्ध करना कठिन है। वैसे वे बिलकुल स्पष्ट प्रतीत होते हैं। ये तथ्य इतने सरल हैं कि यूक्लिड ने इन्हें स्वयंसिद्ध मान लिया और इन्हें स्वयं तथ्य कहा है। इन्हीं तथ्यों पर ज्यामिति के प्रमेयों का प्रमाण निर्भर है। वे तथ्य निम्नलिखित हैं :
१. वे वस्तुएँ, जो एक ही वस्तु के बराबर हों, आपस में भी बराबर होती हैं।
२. यदि बराबर वस्तुओं में बराबर वस्तुएँ जोड़ दी जायँ तो योगफल बराबर होते हैं।
३. यदि बराबर वस्तुओं में से बराबर वस्तुएँ घटा दी जायँ तो शेषफल बराबर होते हैं।
४. बराबर वस्तुओं के समान गुने बराबर होते हैं।
५. यदि दो रेखाओं को तीसरी रेखा काटे और एक ओर के अंत:कोणों का योग दो समकोण से कम हो तो जिधर जोड़ कम है उधर ही दोनों रेखाएँ बढ़ाई जाने पर एक बिंदु पर मिलेंगी।
६. इसी प्रकार रचनाकार्य में भी एक रचना से दूसरी रचना कर सकते हैं, परंतु अंत में कुछ ऐसी रचनाओं पर पहुँचते हैं जिनका प्रयोग दूसरे प्रयोगों पर निर्भर नहीं करता। इन रचनाओं को भी स्वयं प्रयोग मानकर ही आगे बढ़ सकते हैं। वे हैं :
१. किसी भी बिंदु से एक रेखा खींची जा सकती है।
२. सीमित रेखाएँ दोनों ओर बढ़ाई जा सकती है।
३. एक बिंदु को केंद्र मानकर किसी त्रिज्या का एक वृत्त खींच सकते हैं।
इनके अतिरिक्त वे कोई और तथ्य बिना सिद्ध किए हुए स्वीकार नहीं करते। उपर्युक्त पाँच स्वयं तथ्यों में से चार तो इतने सरल तथा सप्ष्ट हैं कि इन्हें सिद्ध करना अपने हाथ को अपना सिद्ध करने के बराबर है, परंतु पाँचवाँ स्वयंतथ्य स्वयंसिद्ध सा प्रतीत नहीं होता। गणितज्ञों ने इस तथ्य को स्वयंसिद्ध मानने में आपत्ति की और इसे सिद्ध करने के बहुत यत्न किए। इन्हीं यत्नों के फलस्वरूप बड़े बड़े आविष्कार हुए। इसी प्रकार ज्यामिति में नए नए पारिभाषिक शब्दों का उल्लेख होता है। एक शब्द की परिभाषा दूसरे शब्दों की परिभाषा पर निर्भर करती है। अंत में देखते हैं कि ये परिभाषाएँ बिंदु, रेखा और तल की परिभाषाओं पर आधारित हैं। यूक्लिड के अनुसार समतल वह है जिसमें लंबाई चौड़ाई हो, परंतु मोटाई न हो। बहुत से लोग इस परिभाषा पर भी संदेह करने लगे हैं, परंतु थोड़ा मनन करने से यह स्पष्ट हो जाएगा कि परिभाषा ठीक है। उदाहरणार्थ, यदि काँच के एक बरतन में दो ऐसे तरल पदार्थ भर दिए जायँ जो आपस में न मिलते हो तो जब वे स्थिर हो जायँ तब हम देखगें कि एक तल दोनों पदार्थों को अलग करता है। उसमें मोटाई नहीं है। यदि होती तो दोनों तरलों के बीच ऐसा स्थान होता जिसमें न नीचे का पदार्थ होता न ऊपर का, परंतु ऐसा असंभव है। इस उदाहरण से स्पष्ट हो गया होगा कि तल में मोटाई नहीं होती। इसमें केवल लंबाई और चौड़ाई ही होती है। इसी प्रकार धूप में किसी समतल दीवार की छाया देखकर हम कह सकते हैं कि रेखा में चौड़ाई नहीं होती। रेखा तल में स्थित है, अत: तल की मोटाई रेखा की मोटाई हुई। इसलिये रेखा में न मोटाई होती है न चौड़ाई, केवल लंबाई ही होती है। रेखाएँ एक बिंदु पर मिलती हैं तो रेखा की चौड़ाई बिंदु की लंबाई हुई, अर्थात् बिंदु में न लंबाई होती है, न चौड़ाई, मोटाई। केवल स्थान ही होता है।
सभी इस बात से परिचित होंगे कि ज्यामिति में त्रिभुज, वर्ग, वृत्त, शंकु, बेलन इत्यादि के गुणों का अध्ययन होता है१ पुराने समय में कुछ प्रश्नों ने गणितज्ञों को काफी उलझाए रखा। उन प्रश्नों के हलों ने बहुत विचारवर्धन किया, इसमें कोई शंका नहीं, जैसे ऐसा घन बनाना जिसका घनफल दिए घन का दुगुना हो। उस समय रचना का अर्थ पटरी और परकार की सहायता से ही रचना करना समझा जाता था। दूसरा प्रश्न था ऐसा वर्ग बनाना जिसका क्षेत्रफल दिए हुए वृत्त के क्षेत्रफल के बराबर हो। तीसरा प्रश्न था कि एक दिए हुए कोण को तीन बराबर भागों में बाँटना। यह काम पटरी और परकार से असंभव है, परंतु अन्य उपायों से हो सकता है। इन प्रश्नों ने शताब्दियों तक गणितज्ञों को व्यस्त रखा। इनके विवेचन से गणितजगत् का बहुत लाभ पहुँचा, इसमें कोई संदेह नहीं।
एक शंकु को किसी समतल से काटने से जो दीर्घवृत्त, परवलय, तथा अपिरवलय वक्र बनते हैं उनके गुणों का भी यूनानियों ने अध्ययन किया। इन अध्ययनों ने केपलन को अपने नियम ज्ञात करने में बड़ी सहायता दी होगी।
प्रक्षेपीय ज्यामिति (Projective Geometry)--१५वीं शताब्दी तक ज्यामिति में प्राय: नाप संबंधी गुणों का ही अध्ययन होता था, परंतु उसके बाद ऐसे गुणों का भी अध्ययन हुआ जो नाप पर निर्भर नहीं करते; जैसे यदि दो त्रिभुजों के शीर्षबिंदु एक तीन बिंदुगामी रेखा पर हों तो संगत भुजाएँ एक रेखा पर मिलेंगी। इस साध्य ने गणितज्ञों का ध्यान एक अन्य प्रकार की ज्यामिति की ओर आकृष्ट किया जिसे प्रक्षेपीय ज्यामिति कहते हैं। यदि हम किसी दृश्य के चित्र पर ध्यान दें तो अनुभव करते हैं कि उसे देखकर दृश्य का पूरा ज्ञान हो जाता है। परंतु चित्र में वृत्त वृत्त नहीं रहता, न सभी समांतर रेखाएँ समांतर रहती है, न समकोण समकोण ही, बल्कि कभी समकोण न्यून कोण दिखाई देता है, कभी अधिक कोण; फिर भी दृश्य में कुछ ऐसे गुण है कि आकृतियों के बदलने पर भी चित्र से उनका पूरा ज्ञान होता है। ये गुण निश्चर कहलाते हैं। ऐसे ही गुणों का प्रक्षेपीय ज्यामिति में अध्ययन होता है।
मान लें, एक बिंदु ब और एक चतुर्भुज क ख ग घ दिया हुआ है। यदि बिंदु ब से चतुर्भुज के प्रत्येक बिंदु को मिलानेवाली रेखाएँ खींची जायँ और उन्हें बढ़ा दें और फिर एक समतल से इन रेखाओं को काटें तो इस तल पर एक चित्र बनेगा। वह इस चतुर्भुज का प्रक्षेप तथा यह प्रयोग बिंदु ब के सापेक्ष रूपांतरण कहलाएगा। इसी प्रकार दूसरा बिंदु लेकर उसके सापेक्ष इस प्रक्षेप का भी प्रक्षेप निकाल सकते हैं। जो गुण नहीं बदलते उन्हें प्रक्षेप द्वारा किसी सरल बहुभुज में बदलकर अध्ययन करते हैं। ये गुण मूल बहुभुज के लिये भी ठीक होंगे। साथ ही कई रूपांतरण मिलकर एक रूपांतरण प्रयोग के समान होते हैं। इन प्रयोगों का भी अध्ययन इस ज्यामिति का अंग है।
प्रतिलोमीय ज्यामिति (Inversive Gemoetry)--यदि किसी गोले या वृत्त का केंद्र क हो तथा त्रिज्या त्र हो और यदि किसी बिंदु ब की केंद्र क से दूरी र हो और यदि र' दूरी पर रेखा क ब में ब' दूसरा बिंदु हो, जहाँ र१ त्र२ तो ब के किसी बिंदुपथ के संगत ब' का भी पथ होगा। ब' का पथ ब के पथ का प्रतिलोमन (inversion) कहलाता है। प्रत्येक क्षेत्र प्रतिलोमन का अध्ययन ही इस शाखा का ध्येय है।
अ-यूक्लिडीय ज्यामिति (Non-Euclidean Geometry)--यूक्लिड का ५वाँ स्वयंसिद्ध तथ्य ऊपर दिया जा चुका है। इसे स्वयंसिद्ध मानने के लिये गणितज्ञ कभी तैयार नहीं हुए, बल्कि उन्होंने इसे सिद्ध करने के बड़े बड़े यत्न किए; परंतु काई संतोषजनक उत्तर नहीं मिला। अनुसंधान के फलस्वरूप गणित का बहुत विकास हुआ और एक ऐसी ज्यामिति का आविष्कार हुआ जिसने ज्यामिति में पूर्ण क्रांति उत्पन्न कर दी। यूक्लिड ने समतल पर ही सब विवेचन किए, परंतु अब हर प्रकार के तलों पर अलग अलग विवेचनाएँ होती हैं। इसका विवेचन कठिन है, अत: इसके लिये पाठक इस विषय की विशेष पुस्तकों का अवलोकन करें।
निर्देशांक ज्यामिति (Coordinate Geometry)--१७वीं शताब्दी के मध्य में फ्रांसीसी गणितज्ञ डेकार्ट (Descartes) ने ज्यामिति में बीजगणित का प्रयोग कर इसे बहुत शक्तिशाली बना दिया। उसने पहले दो काटती हुई रेखाएँ लीं, जिन्हें अक्ष कहते हैं। किसी बिंदु की इन रेखाओं के समांतर नापी हुई दूरी दो संख्याओं य र से उसका स्थान निश्चय किया। ये रेखाएँ बिंदु के निर्देशांक कहलाती हैं। इन निर्देशांकों की सहायता से प्रत्येक ज्यामितिय तथ्य को बीजगणितीय समीकरण द्वारा प्रदर्शित किया जा सकता है। इस ज्यामिति का कई दिशाओं में विकास हुआ।
पहली दशा में तो ज्यामिति का व्यापक रूप सामने आया, जैसे एक घात का समीकरण एक सरल रेखा प्रदर्शित करता है। इसी प्रकार दो घात का समीकरण एक शांकव (conic) प्रदर्शित करता है। इसी प्रकार तीन, चार और उच्चतर घातों के समीकरणों का अध्ययन होने लगा और उनके संगत वक्रों के गुणों का विवेचन पहले से बहुत सरल हो गया। तल के वक्रों तक ही नहीं, अवकाश (space) के वक्रों का भी अध्ययन संभव हो गया। इसके लिये एक बिंदुगामी तीन समतलों से किसी बिंदु की दूरियों य र ल (x, y, z) न उसका स्थान निश्चित करते हैं और प्रत्येक बिंदुपथ को य, र, ल (x, y, z) में एक समीकरण द्वारा प्रदर्शित करते हैं। इन समीकरणों के विवेचन से तलों ओर वक्रों के गुणों का अध्ययन सरलता से होता है।
दूसरी दिशा में रचना संबंधी प्रश्नों का हल तथा क्रियाएँ बहुत सरल हो गईं। ये क्रियाएँ केवल कुछ समीकरणों के हल पर ही निर्भर हैं, जिसमें बहुत व्यापक प्रश्न सरलता से हल हो जाते हैं; जैसे यदि रेखा क य + ख र + ग = o (ax + by + c = o) किसी वक्र का य२ + खा र२ + २ जा य र + २ छाय + २ चार + ग = o (Ax2 + By2 + 2Hxy + 2Gx + 2F y+c) = o को काटती है, तो इन दोनों समीकरणों के हल उनके कटान बिंदुओं का स्थान निश्चित करेंगे। यदि इन समीकरणों के मूल वास्तविक हैं, तो रेखा वक्र को काटती है। यदि बराबर हैं तो रेखा वक्र को स्पर्श करती है। यदि काल्पनिक हैं तो रेखा वक्र को नहीं काटती, परंतु हम यह कह सकते हैं कि रेखा वक्र को सदैव दो बिंदुओं पर काटेगी, चाहे बिंदु वास्तविक या संपाती हों, अथवा काल्पनिक हों। इसी प्रकार से तथ्य बड़े व्यापक रूप में दिए जा सकते हैं, जो साधारण ज्यामिति में संभव नहीं था।
तीसरी दिशा में निर्देशांक ज्यामिति ने विमिति (dimension) को व्यापक किया। दो संख्याएँ य, र (x, y) दो विमितियों (dimensions) में तथा तीन संख्याएँ (य, र, ल) (x, y, z) तीन विमितियों में किसी बिंदु का स्थान निश्चित करती हैं। अब गणितज्ञों के सामने यह प्रश्न उठा कि चार संख्याएँ य, र, ल, व (x, y, z, t) या पाँच संख्याएँ य, र, ल, व, ह (x, y, z, t, w) क्या प्रदर्शित करेंगी। गणितज्ञों ने तो अमूर्त रूप से अपने मस्तिष्क में बड़ी आसानी से सोच लिया कि चार संख्याएँ चार विमितियों में और पाँच संख्याएँ पाँच विमितियों में किसी बिंदु का स्थान निश्चित करेंगी।
इस प्रकार उन्होंने स विमितियों का विचार भी अच्छी तरह सोच लिया। उन्हें इससे कोई मतलब नहीं कि पार्थिव जगत् में उसका कोई उदाहरण है या नहीं। आइंसटाइन ने अवश्य इस विचार का अपने सापेक्ष सिद्धांत में उपयोग किया और विमिति के विचार का स्पष्टीकरण किया। अब इस उच्च विमिति के विचार का अप्रयुक्त गणित में कुछ कठिन समस्याओं को हल करने में उपयोग करते हैं। जैसे किसी चल तरल पदार्थ के भिन्न भिन्न कणों का स्थान, सात संख्याओं से प्रदर्शित करते हैं। वे हैं क, ख, ग (a, b, c), उसका प्रारंभिक स्थान, तथा तीन वेग, जो य, र, ल (x, y, z) अक्ष के समांतर हों, तथा समय, यह सात विमिति का प्रश्न समझकर हल हो सकता है।
चौथी दिशा में निर्देशांक ज्यामिति ने संख्याओं का व्यापकीकरण किया और काल्पनिक संख्याओं का आविर्भाव हुआ। कल्पनिक बिंदु तथा काल्पनिक वक्र इत्यादि विचारों ने ज्यामिति को बहुत महत्वशाली बना दिया, जिससे व्यापकीकरण में और अधिक सहायता मिली, जैसे अनंत पर दो काल्पनिक बिंदुओं से जानेवाला शांकब वृत्त होता है, इत्यादि।
इसके अतिरिक्त ज्यामिति का विवेचन भिन्न भिन्न प्रकार के निर्देशांकों की सहायता से होने लगा, जैसे समघातीय निर्देशांक, त्रिकोणीय निर्देशांक, स्पर्शीय निर्देशांक इत्यादि।
अवकल ज्यामिति (Differential Geometry)--निर्देशांकों के प्रयोग के लगभग ५० वर्ष बाद ही कलन (calculus) का प्रयोग भी ज्यामिति में होने लगा। इस प्रयोग ने ज्यामिति में नई नई विचारधाराएँ उत्पन्न कीं। इन्हें ही अवकल ज्यामिति कहते हैं।
यदि किसी
वक्र र =
फ (य) [y
= f(x)] के किसी
बिंदु य, र (x,y)
पर वक्र की एक स्पर्शी
खींची जाय, जो
य (x)
अक्ष के साथ कोण
'क्ष' (q)
बनाती है, तो
कलन की सहायता
से यह सिद्ध होता
कि स्प क्ष = ![]() ।
इस संबंध से स्पर्शी
का समीकरण
।
इस संबंध से स्पर्शी
का समीकरण
![]() हो जाता
है। जहाँ या (X)
रा (Y)
चल निर्देशांक
हैं तथा य, र (x,y)
वक्र के किसी बिंदु
के। इसी प्रकार
अभिलंब का समीकरण
है
हो जाता
है। जहाँ या (X)
रा (Y)
चल निर्देशांक
हैं तथा य, र (x,y)
वक्र के किसी बिंदु
के। इसी प्रकार
अभिलंब का समीकरण
है
![]()
![]() ।
।
इनकी सहायता
से स्पर्शी अभिलंब,
केंद्रज, प्रतिकेंद्रज,
अन्वालोप, अनंतस्पर्शी
इत्यादि के अध्ययन
में बड़ी सुगमता
हो जाती है।
कलन से ज्यामिति
में कई नई विचारधाराएँ
उत्पन्न हुईं, जैसे
वक्र का आश्लेषी
समतल (osculating
plane), आश्लेषी
वृत्त (osculating
circle), आश्लेषी
गोला (oscultaing
sphere), वक्र परिवार
का सीमावक्र, तलों
का समीतल इत्यादि।
कलन ने ज्यामिति
को एक और विशेष
विचार दिया,
वह है वक्रता का।
किसी वक्र की वक्रता
उपर्युक्त कोण
क्ष (q)
के वक्र की लंबाई
व (s)
के सापेक्ष बदलने
की दर है, अर्थात्
वक्रता = ![]() ।
इसी प्रकार वक्र
की ऐंठन का विचार
भी दिया। वक्र की
वक्रता और ऐंठन
की सहायता से
अवकाश में वक्र खींचने,
या वक्र की कल्पना
करने में, बड़ी
सहायता मिलती
है१ यदि फ (य, र,
ल) = o [f (x,y,z)
= 0]
कोई तल हो
तो इसके स्पर्शी
तल का समीकरण
है
।
इसी प्रकार वक्र
की ऐंठन का विचार
भी दिया। वक्र की
वक्रता और ऐंठन
की सहायता से
अवकाश में वक्र खींचने,
या वक्र की कल्पना
करने में, बड़ी
सहायता मिलती
है१ यदि फ (य, र,
ल) = o [f (x,y,z)
= 0]
कोई तल हो
तो इसके स्पर्शी
तल का समीकरण
है
![]()
![]()
![]() तथा
अभिलंब है
तथा
अभिलंब है 
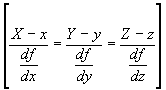 ।
।
इनकी सहायता से तलों के केंद्रज, प्रतिकेंद्रज, अन्वालोप इत्यादि के गुणों का अध्ययन होता है। यदि तल के किसी बिंदु पर खींचे गए अभिलंब से होकर जानेवाले समतल खींचे जायँ तो प्रत्येक समतल तल को एक वक्र में काटता है१ इन वक्रों में से प्राय: एक वक्र की वक्रता न्यूनतम तथा एक की अधिकतम होती है। इनकी विशेषता यह है कि न्यूनतम और अधिकतम वक्रतावाले वक्रों के तल एक दूसरे पर लंबे होते हैं।
इनकी वक्रता
यदि ![]() और
और ![]() हो, तो तल की
वक्रता
हो, तो तल की
वक्रता ![]() से प्रदर्शित करते
हैं। इस प्रकार तल
तीन कक्षाओं में
बॉटें जा सकते
हैं-एक ऐसी जिनकी
वक्रता धन है, दूसरी
वे जिनकी वक्रता
ऋण है और तीसरी
वे जिनकी वक्रता
शून्य है। ये तल
क्रमश: दीर्घवृत्तीय,
अतिपरवलीय और
परवलीय तल
कहलाते हैं। अयूक्लिडीय
ज्यामिति में इन्हीं
तलों पर भिन्न
भिन्न ज्यामितियों
की विवेचना
होती है।
से प्रदर्शित करते
हैं। इस प्रकार तल
तीन कक्षाओं में
बॉटें जा सकते
हैं-एक ऐसी जिनकी
वक्रता धन है, दूसरी
वे जिनकी वक्रता
ऋण है और तीसरी
वे जिनकी वक्रता
शून्य है। ये तल
क्रमश: दीर्घवृत्तीय,
अतिपरवलीय और
परवलीय तल
कहलाते हैं। अयूक्लिडीय
ज्यामिति में इन्हीं
तलों पर भिन्न
भिन्न ज्यामितियों
की विवेचना
होती है।
[झम्मनलाल श्न्नर्मा