ज़ेमान प्रभाव (Zeeman Effect) सन् १८९६ में ज़ेमान (Zeeman) ने सोडियम ज्वाला को एक प्रबल विद्युतच्चुंबक के दो ध्रुवों के मध्य रख कर उसके प्रकाश की जाँच की और यह खोज निकाला कि वर्णक्रम की दोनों तीव्र पीली रेखाएँ कुछ चौड़ी हो गईं। यदि वर्णक्रमदर्शी की विभेदन-क्षमता काफ़ी अधिक हो तो चुंबकीय क्षेत्र में रखे प्रकाश स्त्रोत की प्रत्येक वर्णक्रम रेखा कई घटक रेखाओं में विभाजित हो जाती है। इस घटना को ज़ेमान प्रभाव कहते हैं। सन् १८९२ में फैराडे ने यही प्रभाव देखने का असफल प्रयत्न किया था। अवशोषक माध्यम को चुंबकीय क्षेत्र में रखने पर अवशोषित रेखाओं का घटकों में विभाजन होता है। इसे व्युत्क्रम (inverse) ज़ेमान प्रभाव कहते हैं।

ज़ेमान प्रभाव देखने के लिये वर्णक्रम रेखाओं को एक उच्च विभेदक क्षमतावाले उपकरण, जैसे लुमर-गेहरके पट्ट (Lummer-Gehrcke plate) और नियम विचलन वर्णक्रमलेखी (spectrograph) के योग द्वारा निरीक्षण किया जाता है। चुंबकीयक्षेत्र की अभिलंब दिशा में निरीक्षण से अनुप्रस्थदृश्य तथा समांतर दिशा में निरीक्षण से अनुदैर्ध्य,दृश्य, प्राप्त होता है। अनुदैर्ध्यदृश्य के लिये चुंबक के एक ध्रुव के मध्य में चुंबकीय क्षेत्र के समांतर एक नाली या सुरंग का होना आवश्यक है।

चित्र १. प्राकृत ज़ेमान प्रभाव

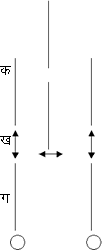
क. बिना चुंबक क्षेत्र के; ख. अनुप्रस्थदृश्य तथा ग. अनुदैर्ध्यदृश्य।

लोरेंट्स (Lorentz) ने अपने द्रव्य और विकिरण के इलेक्ट्रान सिद्धांत के आधार पर इसकी व्याख्या की और यह भविष्यवाणी को कि ये वर्णक्रम रेखाएँ चुंबकीय क्षेत्र द्वारा ध्रुवित हो जानी चाहिए। अनुदैर्ध्यदृश्य में इन रेखाओं में वृत्तीय ध्रुवण और अनुप्रस्थदृश्य में रैखिक ध्रुवण होना चाहिए। इन भविष्यवाणियों का ज़ेमान ने सत्यापन किया। लोरेंट्स ने अपने सिद्धांत द्वारा यह दिखाया कि प्रकाश की वर्णक्रम रेखा को चुंबकीय क्षेत्र की लंबदिशा में देखने पर तीन घटक रेखाएँ दृष्टिगोचर होनी चाहिए (देखें चित्र १ ख)। मध्य की रेखा पूर्व, या मूल, रेखा की जगह पर होती है, अतएव इसकी वही आवृत्ति v_o होगी जो मूल रेखा की है। इसका ध्रुवण रैखिक होगा और इसका विद्युद्दिष्ट (electric vector) चुंबकीय क्षेत्र की समांतर दिशा में कंपन करेगा। इसे p अथवा p घटक कहते हैं। बाहर की दोनों घटक रेखाएँ, मध्य की रेखा से बराबर दूरी पर Dv (नीचे देखें) परिमाण में हटी होती हैं। अतएव इनकी आवृत्तियाँ v_o+Dv तथा v_o-Dv हैं। दोनों घटकों का ध्रुवण रैखिक होता है तथा इनका विद्युद्दिष्ट चुंबकीय क्षेत्र की अभिदिशा में कंपन करता है। इन्हें b या s घटक कहा जाता है। परंतु प्रकाश को चुंबकीय क्षेत्र की समांतर दिशा में निरीक्षण करने पर मध्य की घटक रेखा अनुपस्थित होती है और केवल बाहर की दो घटक रेखाएँ Dv परिमाण द्वारा हटी हुई देखी जाती हैं। ये घटक रेखाएँ विपरीत दिशाओं में वृत्ताकार ध्रुवित होती हैं (देखें चित्र १ ग)।

आवृत्ति विस्थापन Dv चुंबकीय-क्षेत्र की तीव्रता के अनुपात में होता है१ लोरेंट्स के चिर प्रतिष्ठित सिद्धांत के अनुसार

जिसमें e इलेक्ट्रॉनीय आवेश (स्थिर विद्युत् इकाइयों में), m इलेक्ट्रॉन की द्रव्य मात्रा (ग्रामों में), c प्रकाश वेग तथा H चुंबकीय क्षेत्र अर्स्ट्रेडों (oersteds) में हैं। तरंगसंख्या (, जहाँ शून्य में तरंगदैर्ध्य है) में यह विस्थापन लोरेंट्स इकाई में होगा।

ज़ेमान प्रभाव में जब उपर्युक्त विस्थापन पर केवल तीन घटक रेखाएँ (अनुप्रस्थदृश्य में) देखीं जायँ, उसे प्रकृत ज़ेमान प्रभाव (normal Zeeman effect) कहते हैं तथा उन घटक रेखाओं के नमूने का प्रकृत त्रिक् या लोरेंट्स त्रिक् (normalor Lorentz triplet) कहते हैं। परंतु जब एक वर्णक्रम रेखा कई अधिक घटक रेखाओं में विभाजित हो जाती है, तब उसे अप्रकृत ज़ेमान प्रभाव (anomalous Zeeman effect) कहते हैं, क्योंकि उसकी व्याख्या चिर प्रतिष्ठित सिद्धांत के आधार पर नहीं की जा सकती। प्रकृत ज़ेमान त्रिक् विशेष रूप है और एकक श्रेणी (singlet seres) की वर्णक्रम रेखाओं द्वारा प्रदर्शित किया जाता है, जबकि प्रारंभिक और अंतिम ऊर्जा दशा (energy state) का लैंडे g गुणांक (Lande g factor, नीचे देखें) एक के बराबर होता है। साधारण लोरेंट्स त्रिक् जस्ता (zinc) और कैडमियम (cadmium) के वर्णक्रमों में देखे गए तथा उनके आवृत्तिविस्थापन Dv और H की माप से e/m का परिमाण उपर्युक्त सूत्र द्वारा निकाला गया, जो ऋणाग्र किरणों (cathode rays) द्वारा निकाले हुए e/m के बराबर पाया गया। यह परिणाम ऐक्य तथा अनुदैर्ध्यदृश्य में वृत्तीय ध्रुवण के घुमाव की प्रेक्षित दिशा, इस बात का प्रमाण हैं कि परमाणवीय वर्णक्रम में विकिरण चलायमान ऋणात्मक विद्युत् आवेश द्वारा निकलता है।

प्रेस्टन (Preston) ने अधिक विक्षेपण और विभेदन-क्षमता वाले उपकरणों के प्रयोग द्वारा यह स्थापित किया कि उसी वर्णक्रम रेखाओं की किसी विशिष्ट श्रेणी का ज़ेमीन-घटक-रेखाओं का नमूना एक ही प्रकार का होता है और उस श्रेणी का लक्षण (characteristic) होता है। इस प्रकार ज़ेमान प्रभाव वर्णक्रम विश्लेषण का विशिष्ट साधन बन गया। सन् १९०७ में रूँगे (Runge) ने यह दिखाया कि अप्रकृत ज़ेमान नमूनों की घटक रेखाओं का विस्थापन, प्रकृत त्रिक् रेखाओं के विस्थापन गुणनफल के रूप में प्रकट किया जा सकता है। उदाहरणार्थ (जैसे सोडियम की ५८९६ A रेखा) के p और s घटकों का विस्थापन और लोरेंट्स इकाइयाँ होगा। (जैसे सोडियम की ५८९० A रेखा) के लिये यह विस्थापन लोरेंट्स इकाइयाँ होगा।

परमाणु के दिष्ट (vector) नमूने के आधार पर और एक गुणांक (factor), जिसे अब लैंडे का g गुणांक कहा जाता है, अपने सिद्धांत में लाकर लैंडे ने सभी प्रेक्षित ज़ेमान प्रभावों की व्याख्या की और कुछ की भविष्यवाणी भी की। जिस प्रकार परमाणवीय वर्णक्रम रेखाओं की बहुक (multiplet) सरंचना उसकी ऊर्जा दशा या वर्णक्रमीय तरंग संख्या (spectral term) का विभाजन होने के कारण उत्पन्न हुई कही जाती है, उसी प्रकार एक रेखा का ज़ेमान घटकों में विभाजन होने का कारण चुंबकीय क्षेत्र द्वारा उसकी ऊर्जा दशा का विभाजन होना समझा जाता है। परमाणु के अर्धप्रतिष्ठित माडल में इलेक्ट्रॉन की कक्षक कोणीय गतिमात्रा (orbital angular momentum) को l* दिष्ट द्वारा निरूपित (represent) किया जाता है। यह कोणीय गतिमात्रा के बराबर होगी, जिसमें l कक्षीय क्वांटम संख्या है। इसी प्रकार S* दिष्ट द्वारा भ्रमि (shin) कोणीय गतिमात्रा का वर्णन किया

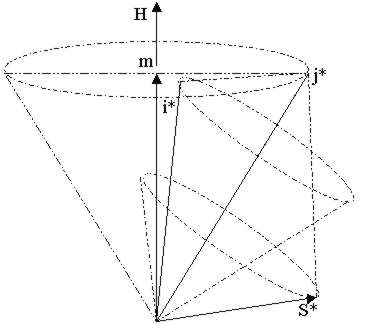
चित्र २. पुरस्सरण (Precession)

क्षेत्र H की दिशा के चतुर्दिक, अकेले संयोजी इलेक्ट्रॉन का चिरसम्मत पुरस्सरण।

जाता है। यह कोणीय गतिमात्रा के बराबर होगी, जिसमें s भ्रमि-क्वांटम संख्या है, जो ऐकिक इलेक्ट्रॉन के लिये है। l* और s* दिष्ट अपने परिणामी दिष्ट j* के चारों ओर एक समान चाल से पुरस्सरण करते हैं और संपूर्ण यांत्रिक गतिमात्रा होगी , जिसमें j आंतरिक (inner) क्वांटम संख्या कहलाता है (देखें चित्र २.)। जब परमाणु को एक निर्बल चुंबकीय क्षेत्र में रखा जाता है, तब संपूर्ण यांत्रिक संवेग से संबंधित चुंबकीय संवेग के कारण वह चुंबकीय क्षेत्र दिशा H के चारों ओर लट्टू की भाँति पुरस्सरण करने लगता है (चित्र २)। इस गति पर क्वांटम शर्ते लगती हैं कि कोणीय गतिमात्रा के चुंबकीय क्षेत्र H की दिशा पर

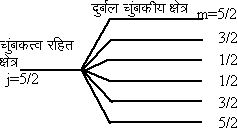
चित्र ३. दुर्बल चुंबकीय क्षेत्र में एक ऊर्जा स्तर का विभाजन

यह रेखाचित्र J = के लिये खींचा गया है।

प्रक्षेपों (projections) के केवल वही परिमाण (value) हो सकते हैं जो के बराबर हों। यहाँ चुंबकीय क्वांटम संख्या । दूसरे शब्दों में j* का क्षेत्र H की दिशा पर प्रक्षेप, -j से +j तक, केवल अर्धपूर्ण संख्याओं (half integral) के बराबर होगा। के लिये देखें चित्र ३। इस प्रकार का क्षेत्र रहित आकाश में एक ऊर्जा स्तर n,l, तथा j तीन क्वांटम संख्याओं द्वारा परिमित किया जाता है, परंतु एक निर्बल क्षेत्र में ऊर्जा स्तर को परिमित करने के लिये इनके अलावा एक चौथी क्वांटम संख्या m, चुंबकीय क्वांटम संख्या, की आवश्यकता होती है। अतएव अवकाश में परमाणु की विशिष्ट दिक्स्थिति (discreteorientation) होने के कारण ऊर्जा स्तरों की संख्या 2j+1 के बराबर होगी। इन स्तरों की पारस्परिक दूरी का परिमाण चुंबकीय क्षेत्र की तीव्रता और चुंबकीय घूर्ण पर निर्भर है। अत: किसी प्रयोग में, एक परमाणु के, जिसपर प्रेक्षण किया जा रहा है, सब स्तरों के लिये क्षेत्र तीव्रता H वही है, ज़ेमान विस्थापन को लोरेंट्स इकाइयों में प्रकट किया जा सकता है। यह विस्थापन mgLcm^-1 के बराबर होता है, जिसमें g निम्नलिखित रीति से प्राप्त प्रसिद्ध लैंडे g गुणांक है:

एक ऊर्जा स्तर से दूसरे स्तर के लिये इलेक्ट्रॉन संक्रमण (transition) के लिये वरण नियम है:

ज़ेमान नमूने की गणना शीघ्रतापूर्वक करने का एक ढंग नीचे दिया गया है, जो तथा संक्रमणों (transition) उदाहरण लेकर किया गया है :

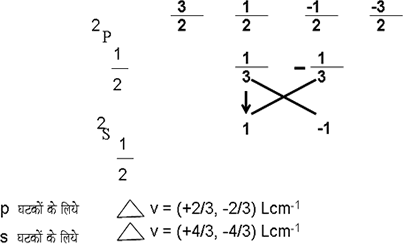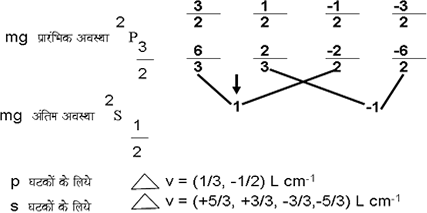
इसके संक्रमण और फलस्वरूप उत्पादित ज़ेमान नमूने चित्र ४ में दिखाए गए हैं, जिसमें रेखा की तीव्रता को रेखा की ऊँचाई द्वारा प्रकट किया गया है तथा P और S घटकों को क्षितिज रेखा के क्रमश:

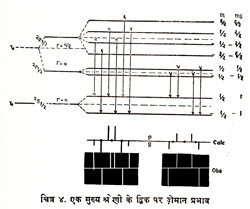
चित्र ४. एक मुख्य श्रेणी के द्विक पर ज़ेमान प्रभाव

तीर विभिन्न ज़ेमान अवयवों के संक्रमण व्यक्त करते हैं और उन संक्रमणों की सापेक्ष तीव्रता तीरों के ऊपर पूर्णांकों द्वारा दी गई हैं। बाईं ओर का तीरों का समूह (जैसे सोडियम ५८९६ ) रेखा के लिये और दाहिनी ओर का समूह (सोडियम ८५९६ A° ) रेखा के लिये है। चित्र का निचला भाग परिकलन और निरीक्षण द्वारा प्राप्त परिणामी ज़ेमान प्रभाव व्यक्त करता है।

ज़ेमान प्रभाव तभी देखा जाता है जब बाह्य चुंबक क्षेत्र इलेक्ट्रॉन की भ्रमि (spin) तथा कक्षा (orbit) गतियों द्वारा उत्पन्न किए गए आंतरिक क्षेत्र से निर्बल होता है; परंतु जब बाह्य क्षेत्र इन आंतरिक क्षेत्रों से अति प्रबल होता है तब ज़ेमान प्रभाव पाश्चन-बैक प्रभाव (Paschen-Back effect) में परिणत हो जाता है। यह प्रभाव सन् १९१२ में पाश्चन और बैक ने देखा और यह पाया कि बहुत अधिक तीव्र चुंबक क्षेत्र में प्रकृत ज़ेमान घटक नमूना प्रकृत ज़ेमान घटक नमूना प्रकृत ज़ेमान त्रिक् में बदल जाता है। इस प्रभाव का कारण यह है कि निर्बल क्षेत्र में I* और S* दिष्ट अपने परिणामी दिष्ट j* के चारों ओर पुरस्सरण करते हैं, परंतु प्रबल क्षेत्र में I* और S* का पारस्परिक बंधन खुल जाता है और दोनों स्वतंत्र रूप से क्षेत्रदिशा के चारों ओर पुरस्सरण करते हैं। सौभाग्य से अधिकतर परमाणुओं में उसके लिये पर्याप्त रूप से प्रबल बाह्य क्षेत्र साधारणतया नहीं उत्पन्न किया जा सकता है, नहीं तो j और g का अलग अलग पता लगाना संभव न होता और ज़ेमान प्रभाव का वर्णक्रम विश्लेषण में प्रयोग न हो पाता, क्योंकि अप्रकृत ज़ेमान घटकों के विभेदन से दोनों संक्रमण संबंधित स्तरों के j परिमाण का (घटकों की संख्या से) तथा g की संख्या का (विस्थापन से) पूरा पूरा पता लग जाता है। इसी लिये ज़ेमान प्रभाव वर्णक्रम विश्लेषण और परमाणुओं और आयनों (ions) की इलेक्ट्रॉन रचना का पता लगाने का मुख्य साधन है। सूर्य और तारों में (stars) कुछ रोचक गुणों की खोज ज़ेमान प्रभाव की सहायता से ही की जा सकी है।

संo ग्रंo -- ज़ेमान पीo : फिल्o मैगo ५,४३,२२६, १८९७; वही : रिसचैंज़ इन मैग्नटो-ऑप्टिक्स (लंदन, १९१३); बैक, ईo और लैंड, एo : ज़ेमान एफेक्ट अंड मल्टिप्लेट स्ट्रक्टूर डेर स्पेक्ट्रेलिनिएन; पाश्चन और बैक : ऐनo डिo फिज़िo ३९, ८९७, १९१२ तथा ४०, ९६०, १९१३; इवाइट, ईo एचo : ईट्रोडक्शन टु ऐटॉमिक स्पेक्ट्रा, १९३४, मेंकग्रॉ हिल। [अजितराम वर्मा]