क्षेत्रमिति और आयतनमिति (Mensuration) गणित की वह शाखा जो लंबाइयों, क्षेत्रफलों और आयतनों की यथार्थ अथवा सन्निकट मापों से संबंधित है। इस अनुच्छेद में मुख्यत: सूत्र दिए गए है; इनकी उपपत्तियाँ सामान्यता रेखागणित अथवा त्रिकोणमिति और कोई कलन गणित के विषयांग हैं।

1. प्राथमिक समतल क्षेत्रफल और लंबाइयाँ-किसी लंबाई के एकक (इंच, फुट, गज, मील आदि; अथवा सेंटीमीटर, मीटर आदि) के क्षेत्रफल का एकक उस वर्ग का क्षेत्रफल है जिसकी भुजा मनोनीत लंबाई के बराबर है। इस वर्ग के क्षेत्र फल को एक वर्ग एकक, अर्थात् एक वर्गइंच, एक वर्गफुट, एक वर्गमीटर आदि कहते हैं। इन एककों में किसी आयत का क्षेत्रफल उसकी लंबाई में एककों की संख्या को उसकी चौड़ाई के एककों की संख्या से गुणा करने पर प्राप्त होता है (देखें चित्र १.)



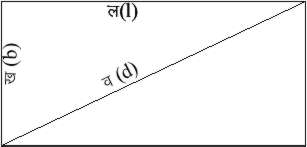
मान लीजिए, आयत की लंबाई १ है और चौड़ाई b है तो उसका

क्षेत्रफल A=1xb

और विकर्ण d=� (1²+b²)

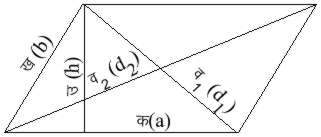
ऐसे चतुर्भुज को समांतर चतुर्भुज कहते हैं जिसकी संमुख भुजाएँ समांतर हैं। इसका क्षेत्र फल प्रकट करने के लिये किन्हीं दो समांतर भुजाओं को आधार माना जाय तो उनके बीच की लांबिक दूरी को ऊँचाई कहा जाता है। यदि आधार की लंबाई a तथा ऊँचाई h है तो क्षेत्रफल A=a h

यदि समांतर चतुर्भुज के विकर्ण d₁ तथा d₂ है तो d₁²+d₂²=2(a²+b²) जहाँ a तथा b उसकी भुजाएँ हैं।

किसी भी विकर्ण से समांतर चतुर्भुज दो समान त्रिभुजों में विभाजित हो जाता है और विलोमत: किसी भी त्रिभुज को एक समांतर चतुर्भुज के समद्विभाजन से प्राप्त हुआ माना जा सकता है। इस प्रकार समांतर चतुर्भुज का आधार और उसकी ऊँचाई उसके समद्विभाजन से प्राप्त किसी भी त्रिभुज का आधार और उसकी ऊँचाई बन जाते हैं। अतएव त्रिभुज के क्षेत्रफल के लिए सूत्र A=� a h (देखें चित्र २.)



प्राय: त्रिभुज की भुजाओं से क्षेत्रफल निकालने की आवश्यकता पड़ती है। इसके लिये सूत्र यह है : A= �s(s-a) (s-b) (s-c)

जहाँ त्रिभुज की भुजाएँ a, b, c हैं और s=� (a+b+c)*



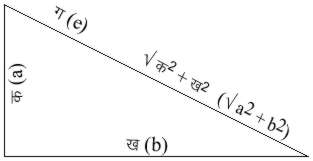
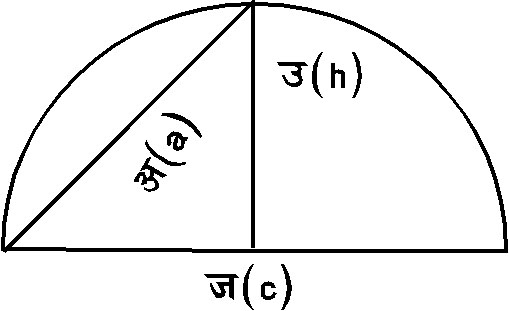
यदि त्रिभुज का एक कोण समकोण है और समकोणवाली भुजाओं की लंबाइयाँ a तथा b है तो क्षेत्रफल A=� ab होगा। तीसरी भुजा (कर्ण) c = �(a² +b²) (देखें चित्र ३.)। इस संबंध की खोज पाइथैगोरस ने ५०० ई. पू. में की थी। उसी के नाम से यह प्रमेय विख्यात है। विलोमत:, यदि यह संबंध किसी त्रिभुज की भुजाओं से संतुष्ट होता है तो वह त्रिभुज समकोण त्रिभुज है। इस सूत्र का उपयोग करके समतल मैदान में फीते की सहायता से समकोण बनाया जा सकता है। यदि १२ गज लंबे फीते के सिरों को मिलाकर उसे ३, ४, ५ गज की भुजाओंवाले त्रिभुज के रूप में तान दिया जाए तो एक समकोण त्रिभुज बन जाएगा क्योंकि

३^२ + 4² = 5²



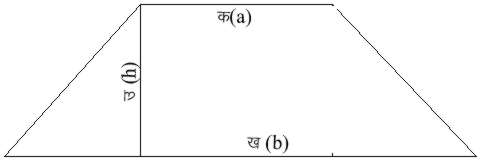
ऐसे चतुर्भुज को जिसकी दो भुजाएँ समांतर होती हैं समलंब कहते हैं। यदि समांतर भुजाओं की लंबाइयाँ a तथा b हैं और उनके बीच की लांबिक दूरी h है तो समलंब का क्षेत्रफल (देखें चित्र ४.)।

A = � (a+b) h

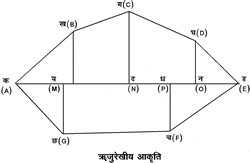
2. व्यापक बहभुज-----पूर्वोक्त आकृतियों के अतिरिक्त यदि कैसा भी बहुभुज A B...G दिया हो तो उसका क्षेत्रफल ज्ञात करने के लिये कोई विकर्ण, मान लें AE खींचे और बहुभुज के AE के अतिरिक्त अन्य शीर्षों से इसपर लंब BL, CN इत्यादि खींचें।

इस प्रकार बहुभुज त्रिभुजों और समलंबों में विभक्त हो जाता है और इनके क्षेत्रफलों का योगफल बहुभुज का क्षेत्रफल है (देखें चित्र ५.)।



(२) वृतत

3. परिधि और वृत्तीय चाप की लंबाइर्-वृत्त की परिधि व्यास की p गुनी होती हैं। p एक अपरिमेय बीजातीत संख्या है (देखें संख्या पर लेख)।

चार दशमलव स्थानों तक शुद्ध p का मान ३.१४१६ है, इससे भी अधिक शुद्ध मान ३५५/११३ है (इसे स्मरण रखने के लिये ध्यान रखें कि हर के आगें अंश लिखने पर प्रथम तीन विषम संख्याओं के जोड़े बन जाते हैं)।

सामान्यता p को २२/७ मान लिया जाता है, जो यथार्थ मान से लगभग .०४ प्रतिशत अधिक है। क्योंकि वृत्त के किन्ही दो समान लंबाई के चापों से केंद्र पर समान कोण बनते हैं, इसलिए वृत्तीय चाप की लंबाई उससे केंद्र पर बने कोण की

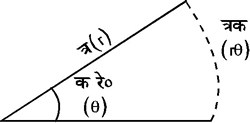
समानुपाती है। क्योंकि त्रिज्या चान की लंबाई उससे केंद्र पर १८० का ऋजुकोण बनानेवाला चाप, अर्धपरिधि, लंबाई p r का है, इसलिए केंद्र पर, q का कोण बनानेवाले चाप की लंबाई p r q /180 है। इस प्रकार त्रिज्या के बराबर की लंबाई का चाप वृत्त पर 180/p अंश का कोण बनाएगा। इस कोण को रेडियन कहते हैं, अर्थात् p रेडियन १८०। यदि केंद्र पर बने कोण की माप q रेडियन होती चाप r=q जहाँ r वृत्त की त्रिज्या है (देखें चित्र ६ .)।



कभी कभी चाप के केंद्र की स्थिति जानने में असुविधा होती है; तब उसके सिरों को मिलानेवाली ऋजु रेखा, अर्थात् उसकी जीवा c और उसके एक सिरे से चाप के मध्य बिंदु तक की ऋजु रेखा a के पदों में चाप की लंबाई १ निम्नांकित संनिकट सूत्र से ज्ञात की जा सकती है :

1- 8/3 a-1/3 c

इस सूत्र से .१% की यथार्थता का मान तब तक मिलता है जब तक कि चाप के मध्यबिंदु की जीवा के मध्यबिंदु से दूरी c से कम अर्थात् h<1/5c है। यदि ऐसा ने हो तो चाप के अलग अलग खंडों की लंबाइयाँ इस सूत्र से निकालकर उन्हें जोड़ देना चाहिए (देखें चित्र ७)।

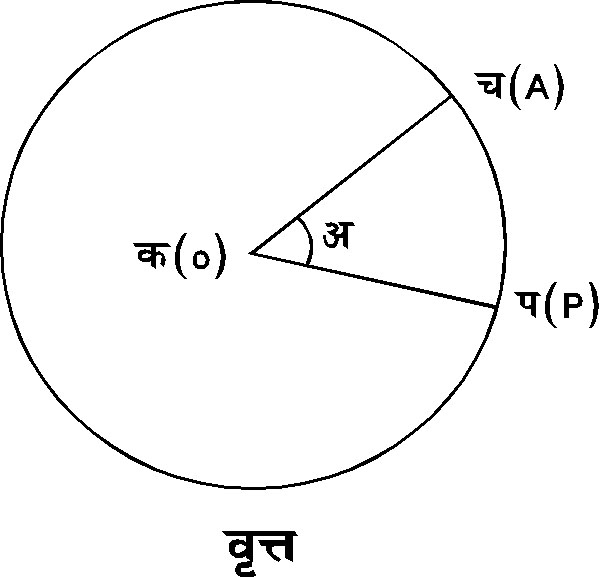
4. द्वैत्रिज्य और वृत्तखंडों के क्षेत्रफल्ा-त्रिज्या r के वृत्त का क्षेत्रफल A=pr²। वृत्त की किंन्हीं दो त्रिज्याओं और उनके सिरों को मिलानेवाली चाप से घिरा हुआ क्षेत्र द्वैत्रिज्य कहलाता है। त्रिज्याओं के बीच के कोण को द्वैत्रिज्य का कोण कहते हैं (चित्र ८. में A O P)। एक वृत्त में समान कोणों के द्वैत्रिज्यों के क्षेत्रफल समान होते हैं। इस तथ्य के आधार पर यह सिद्ध किया जा सकता है कि द्वैत्रिज्य का क्षेत्रफल उसके कोण का समानुपाती है। अतएव यदि वृत्त की त्रिज्या r है तो कोण q रेडियनवाले द्वैत्रिज्य का क्षेत्रफल A = �r²q।

यदि द्वैत्रिज्य कोण q है, तो A=pr² q/360। किसी वृत्तीय चाप और उसकी जीवा से घिरे हुए क्षेत्र को वृत्तखंड कहते हैं। चाप और वृत्त के मध्यबिंदुओं को मिलानेवाली रेखा को वृत्तखंड की ऊँचाई कहते हैं। अनुच्छेद ३ के अंतिम चित्र में वृत्तखंड की जीवा c, ऊँचाई h और अर्धताप की जीवा a है। वृत्तखंड क्ष A के लिए एक संनिकट सूत्र यह है :

A-h (2/5c+1⁸₅a)

जब तक h<1/5c

। इस सूत्र में .०३ % प्रतिशत के लगभग त्रुटि रहती है।

(३) क्षेत्रकलन


5. समतल वक्ररेखीय आकृति का क्षेत्रफल-ऐसी समतल आकृतियों क्षेत्रफल की गणना, जो एक या अधिक रेखाओं (ऋजु या तक्र) से घिरी हों, निर्देशांक ज्यामिति और कलन की विधियों से की जा सकती है। सामान्यता आकृति के समतल में पहले दो निर्देक्षाक्ष चुने जाते हैं। फिर आकृति की परिसीमा को ऐसे खंडो में विभक्त किया जाता है कि उनमें से प्रत्येक Y-अक्ष की समांतर रेखा द्वारा एक से अधिक बिंदु पर न कटता हो और X- से बिलकुल न कटता हो। ऐसे प्रत्येक खंड का निरूपण समीकरण y=fx से किया जा सकता है। यदि इसके सिरों के भुज a तथा b हैं तो कोटियों x=a; x=b; वक्र y=f(x) और (X-) अक्ष से घिरे हुए क्षेत्र को क्षेत्रफल।

A= abf (x) dx

इस सूत्र से प्राप्त विविध खंडो के क्षेत्रफल को जोड़ और घटाकर अभीष्ट क्षेत्रफल ज्ञात किया जा सकता है।

6. संनिकट गणना-यदि फलन f (x) का समाकलन कठिन तथा अज्ञात हो, या वक्र का समीकरण ज्ञात न किया जा सकता हो, तो संनिकट गणना द्वारा क्षेत्रफल प्राप्त किया जाता है। संनिकट गणना के कई सूत्र हैं। इन सबका आधार यह है कि वक्र को समदूरस्थ कई एक कोटियों से विभक्त किया जाता है। जिन बिंदुओं पर ये कोटियाँ वक्र को काटती हैं उनमें दो दो या तीन तीन ............ पर समीकरण

(y=a₀+a1x+a²x²+...)

7. वाले वक्रों का आसंजन किया जाता है और प्रत्येक खंड का क्षेत्रफल कोटियों के पदों में प्रकटकर उनके योगफल से अभीष्ट सूत्र मिल जाता है।

जहाँ h एच दो क्रमागत कोटियों के बीच की दूरी है और b-a=nh।

बहुफलक पर स्थित दो फलकों की प्रतिच्छेद रेखा को कोर कहते हैं; दो कोरों के प्रतिच्छेदबिंदु को शीर्ष कहते हैं। समपार्श्व के समांतर सिरों के बीच की लांबिक दूरी को समपर्श्व की ऊंचाई कहते हैं। यदि समपार्श्व के आधार का क्षेत्रफल A और समपार्श्व की ऊंचाई h है, तो उसका आयतन Ah। विशेषत:, यदि घनाभ की लंबाई, चौड़ाई और ऊँचाई क्रमानुसार a,b,c है तो उसका आयतन =a b c। घनाभ की तीन संगामी कोरों के सर्वनिष्ठ शीर्ष को शेष तीन कोरों के शीर्ष से मिलाने पर एक विकर्ण मिलता है। इसकी लंबाई �(a²+b²+c²)

यदि लंब समपार्श्व के आधार की परिमाप p है और आधार पर लंब कोरों की लंबाई k है तो समपश्वर का पर्श्वापृष्ठ =p k। विशेषत: घनाभ का पृष्ठ =2 (ab+bc+ca) जहाँ a,b,c घनाभ की कोरें हैं।

(८) सूचीस्तंभ-यह बहुफलक सूचीस्तंभ कहलाता हे जिसमें एक फलक, जिसे आधार कहते हैं, बहुभुज हो ओर शेष फलक ऐसे त्रिभुज हो जिनका एक शीर्ष सबमें सर्वनिष्ठ हो । इस शीर्ष को सूचीस्तंभ का शीर्ष कहते हैं शीर्ष से आधार पर खींचे गए लंब की माप सूचीस्तंभ की ऊँचाई है। यदि सूचीस्तंभ के आधार का क्षेत्रफल A और उसकी ऊँचाई h है तो उसका आयतन। ऐसे सूचीस्तंभ को लंबसूचीस्तंभ कहते हैं जिसका आधार या तो कोई सम बहुभुज हो या आयत और आधार के केंद्र को शीर्ष से मिलानेवाली रेखा आधार पर लंब हो। लंबी सूचीस्तंभ में शीर्ष को आधार की एक भुजा के मध्यबिंदु से मिलाने वाली रेखा को तिर्यक ऊंचाई कहते हैं। यदि किसी लंब सूचीस्तंभ के आधार की परिमाप p है और तिर्यक ऊंचाई १ है, तो उसका पार्श्वपृष्ठ =�01 ।

यदि कोर a है तो ऊंचाई =a�2/3 पृष्ठ =a²�3 तथा आयतन = 1/3a³�2

समपर्श्वाभ------यदि किसी बहुफलक के सभी शीर्ष दो समांतर समतलों में हों तो वह एक समपार्श्वाभ कहलाता है। इन समांतर समतलों में स्थित फलकों को आधार और अन्य फलकों को पार्श्वाफलक कहते हैं। आधारों में से एक कोर मात्र भी हो सकती है और केवल एक बिंदु भी। समपार्श्व और सूची स्तंभ का छिंतक (अर्थात सूचीस्तंभ के आधार ओर उसके समांतर समतल के बीच का खंड) दो आधारवाले समपार्श्वाभ हैं। सूचीस्तंभ स्वयं ऐसा समपार्श्वाभ हैं जिसका एक आधार बिंदुमात्र है। समपार्श्वाभ के पार्श्वफलक या तो चतुर्भुज होंगे या त्रिभुज। आधार वाले समांतर समतलों के बीच की दूरी समपार्श्वाभ की ऊँचाई है। इस ऊँचाई के समद्विभाजक, आधार के समांतर, समतल से समपार्श्वाभ की काट मध्य काट कहलाती है। यदि आधारों के क्षेत्रफल A₁..A₂तथा मध्यकाट का क्षेत्रफल Am और ऊँचाई h है तो

समपार्श्वाभ का आयतन =1/6h (A₁+4A_m+A₂)

यह अत्यंत व्यापक सूत्र है। यदि एक आधार केवल कोर या शीर्ष मात्र हो तो उसका क्षेत्रफल शून्य मान लेना चाहिए। पीपे (drum) आदि बहुत से ऐसे ठोसों का भी संनिकट आयतन इस सूत्र से ज्ञात हो जाता है जो यथार्थत: समपार्श्वाभ नहीं है। सूचीस्तंभ के छिंतक के लिए यह सूत्र सरल होकर 1/3h {A₁+A₂+�(A₁A₂} हो जाता है।

(१०) स्फान-----यदि समपार्श्वाभ का एक आधार आयत है और दूसरा आधार इस आयतवाले समतल के समांतर एक कोर है तो एक स्फान प्राप्त होता है। यदि स्फान की ऊंचाई (अर्थात आधार से कोर तक की दूरी) h है, कोर की माप १, उसके समांतर आधार की लंबाई a तथा आधार की चौड़ाई ख b है, तो स्थान का आयतन 1/6bh (2a+1)।

(१२) बेलन-------ऐसे ठोस को बेलन कहते हैं जो एक बंद बेलनीय तल और दो समांतर तलों से घिरा हो। समतल फलकों को बेलन के आधार या सिरे और बेलनीय तल को पार्श्वपृष्ठ या वक्रपृष्ठ कहते हैं। आधारों के बीच की लांबिक दूरी को बेलन की ऊँचाई और आधार के बीच जनक की माप को बेलन की लंबाई कहते हैं। यदि लंब काट क्षेत्रफल A_c और परिमाप P_c की है तथा बेलन की लंबाई १ है, तो बेलन का वक्रपृष्ठ =1p_c आयतन A_c1=Ah जहाँ A आधार का क्षेत्रफल है और h बेलन की ऊँचाई है।

बेलन का सरलतम और समान्यतम रूप लंबवृतीय बेलन है, जिसमें लंब काट और सिरे समान वृत्त हैं। यदि वृत्त की त्रिज्या r और ऊंचाई h है तो लंब वृत्तिय बेलन का

आयतन p r²h;

वक्रपृष्ठ 2prh

यदि लंब बेलन के सिरे सकेंद्र वक्र हैं, तो सिरों के केंद्रों को मिलाने वाली रेखा को बेलन का अक्ष कहते हैं। किसी लंबवृत्तीय बेलन से उसी अक्ष वाला एक छोटा लंबवृत्तीय बेलन निकाल लेने पर रिक्त बेलन मिलता है। नल आदि रिक्त बेलन के आकार होते हैं। यदि रिक्त बेलन के बाह्य पृष्ठ की त्रिज्या r₁ भीतरवाले की r₂और ऊंचाई h है तो उसके द्रव्य का आयतन =p (r₁²-r²₂)h और उसकी धारिता (आयतन) = p r₂²h ।

१३. शंकु-जब कोई ऋजु रेखा इस प्रकार चलती है कि वह सदा एक स्थित बिंदु से ओर एक दिए हुए वक्र के विभिन्न बिंदुओं से होकर जाय तो शांकव तल का जननहोता है। रेखा की विभिन्न स्थितियों को जनक कहते हैं और स्थित बिंदु को शीर्ष। नियता की परिभाषा पूर्ववत है। शीर्ष के एक ओर के बंद शांकव पृष्ठ और एक समतल से घिरे हुए ठोस को शंकु कहते हैं: पृष्ठ का समतल भाग आधार है और शीर्ष से आधार की लंबिक दूरी शंकु की ऊँचाई है। यदि आधार का क्षेत्रफल A है और शंकु की ऊँचाई h है तो शंकु का आयतन =1/3 Ah। यदि शंकु का आधार (त्रिज्या r का) वृत्त है ओर शीर्ष को आधारकेंद्र से मिलानेवाली रेखा आधार लंब पर है, तो शंकु लंबवृत्तिय शंकु कहलाता है। शीर्ष को आधार की परिधि के किसी बिंदु से मिलानेवाली रेखा शंकु की तिर्यक ऊँचाई है ओर जो कोण यह आधार के लंब से बनाते हैं शंकु का अर्धशीर्ष कोण है। यदि तिर्यक् ऊँचाई १, अर्धशीर्ष कोण है तो r, h, I, a वक्र पृष्ठ c संपूर्ण पृष्ठ s और आयतन V के कुछ संबंध ये हैं :
h=1 Cos a r=1 Sin a, V=1/3pr²h

c=pr1, S=pr (r+1)

यदि शकुछिंतक के सिरों की त्रिज्याएँ r₁ r₂ लांबिक ऊंचाई h और तिर्यक ऊंचाई १ हैं, तो छिंतक का आयतन =1/3ph (r₁² + r₁ r₂ +r₂² ।

तथा वक्र पृष्ठ =p (r₁ + r₂)।

१४. गोला-----अवकाश में ऐसे बिंदु का पथ जिसकी किसी स्थिर बिंदु से (जिसे केंद्र कहते हैं) दूरी सदा एक अचर राशि r है, एक गोला है और यह अचर दूरी r गोले की त्रिज्या है। गोले का वक्रपृष्ठ एक बंद तल है ओर इसका क्षेत्रफल =4 pr² तथा गोले का आयतन =4/3 r³ । कोई भी केंद्र गामी समतल गोले को त्रिज्या r के दीर्घवृत्त में काटता है। केंद्र से दूरी=p<r वाला समतल गोले को त्रिज्या � (r²-p²) के लघुवृत्त में काटता है। इस समतल से गोले के पृष्ठ का दो खंडों में विभाजन हो जाता है जिनकी ऊँचाइयाँ r- p और r+p हैं। गोलीय खंड के वक्रपृष्टीय भाग को टोपी कहते हैं। यदि गोलीय खंड की ऊँचाई h आधार त्रिज्या r₁ है तो

वक्रपृष्ठ=2prh

और आयतन =h2 (r-1/3h) = 1/6ph (3 r₁²+h²)।

दो समांतर समतलों के बीच गोले के पृष्ठों का भाग कटिबंध कहलाता है। कटिबंध के सिरे वृत्त होते हैं। इनके केंद्रों को मिलानेवाली रेखा कटिबंध की ऊँचाई है। यदि सिरों की त्रिज्याएँ r1r2 और ऊँचाई h है तो कटिबंध का

वक्रपृष्ठ =2prh

और आयतन = 1/6 ph (3r₁²+ 3r₂² +h²)।

गोले के एक ही व्यासवाले किन्हीं दो अर्धवृत्तों से गोलपृष्ठों का जो भाग कटता है वह इंदुक कहलाता है, क्योंकि यह नए चंद्रमा के आकार का होता है। इस वक्रपृष्ठ और अर्धवृत्तों से घिरे हुए ठोस को भी इंदुक कहते हैं इसके समतलीय सिरों के बीच का कोण इंदुक का कोण है। त्रिज्या r के गोले से कोण a वाले इंदुक का

वक्रपृष्ठ =ar²

आयतन = 2/3 ar³

जो ठोस गोले से ऐसे लंबवृत्तीय शंकु द्वारा कटता है जिसका शीर्ष गोले के केंद्र पर है, उसे गोलीय शकल कहते हैं। यह एक गोलीय खंड और एक ऐसे लंबवत्तीय शंकु के योग से बना माना जा सकता है जिसका आधार वही है जो खंड का और शीर्ष गोले का केंद्र है। यदि खंड की ऊँचाई h है आधारत्रिज्या r१और गोले की त्रिज्या r है तो शकल का आयतन =2/3 p r²h और संपूर्ण पृष्ठ pr (2h+r)।

१५. व्यापक सूत्र------पूर्वोक्त ठोसों के अतिरिक्त अन्य ठोसों का आयतन समाकलन द्वारा ही ज्ञात किया जा सकता है। कभी-कभी सरल समाकलन से भी काम चल जाता है, अन्यथा बहुल समाकलन आवश्यक हो जाता है। सरल समाकलन तब पर्याप्त होता है जब ठोस की समांतर काटों में से किसी का क्षेत्रफल उस काट के एक स्थिर बिंदु से दूरी x का कोई समाकलनीय फलन A (x) हो । यदि काटे समतल x=a और x=b के बीच में हैं तो

आयतन=�_a^b A (x) dx

विशेषत: यदि ठोस वक्र y=f (x) के X- अक्ष के परित: घुमाने से बना है, अर्थात एक परिक्रमज ठोस है, और समतल x=a तथा x=b सीमित है, तो ठोस का

आयतन = p �_a^b {f(x)} ² dx

और वक्रपृष्ठ = 2 p �_a^b f(x) � {1+[f’(x)]²}dx

जहाँ f’ (x) = df (x)/dx

क्योंकि किसी बंद समतल से क्षेत्र a के केंद्रव

x,y के लिए सूत्र

है जहां A क्षेत्र का क्षेत्रफल है, इसलिए क्षेत्र a को इसके समतल में स्थित और इससे प्रतिच्छेदन न करनेवाली किसी ऋजु रेखा के परित: चार समकोण या कम घुमाने पर बने हुए ठोस का आयतन A1 जहाँ ल १ केंद्रवपथ की लंबाई है।

इस प्रकार यदि वक्र की परिमाप p है और इसकी परिसीमा का केंद्रव लंबाई १_१ का पथ चलता है तो उत्पादित ठोस का वक्रपृष्ठ =p1₁

सिमसन ओर समलंब नियमों के उपयोग से आयतन समाकलन की संनिकट गणना सुगमतापूर्वक की जा सकती है। इन सूत्रों का उपयोग करने लिए ठोस की काट यदि लगभग वृत्ताकार है तो उसका क्षेत्रफल =p2/4p, जहाँ p काट की परिमाप है।