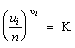 ...
. . . (१)
...
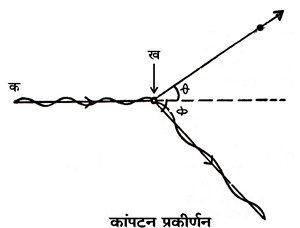
. . . (१)कापंटन परिणाम उच्च कंपन संख्या के विद्युच्चुंबकीय विकिरण की पदार्थ के साथ वह अंत: क्रिया (इंटरऐक्शन, interaction) है जिसमें मुक्त इलेक्ट्रानों से प्रकीर्ण (स्कैटर, scatter) होकर फ़ोटान की ऊर्जा में ्ह्रास हो जाता है और उनके तरंगआयाम में बुद्धि हो जाती है।
इस परिणाम के स्पष्टीकरण के लिए १९२३ ई. में कांपटन और डेबाई ने स्वतंत्र रूप से यह धारणा अपनाई कि किसी दिशा में चलते हुए फ़ोटान में जो ऊर्जा संवेग होता है उनका कुल या केवल थोड़ा सा भाग पर दे सकता है। इससे प्रकीर्ण फ़ोटान की ऊर्जा [ऊ=प्ल आ (E= hv), जिसमें प्ल (h) प्लैंक स्थिरांक है और आ (v) विकिरण की कपंन संख्या हैट आपाती फ़ोटान की ऊर्जा से कम होती है और फ़ोटान से संबंधित तरंगआयाम बढ़ जाता है। स्पष्टत: यह फ़ोटान-इलेक्ट्रान-टक्कर-प्रतिरूप (photen-election collision model) विकिरण के तरंगवाद (वेव थियरी) के एकदम प्रतिकूल है।
सन् १९२४ ई. में बोर (Bohr), क्रेमर्स और स्लेटर ने एक दूसरे प्रतिरूप का सुझाव रखा जो तरंगवाद पर आधारित था। इस प्रतिरूप में ऊर्जास्थिरता और संवेगास्थिरता के नियम विकिरण और इलेक्ट्रान की किसी एकाकी अंत: क्रिया में लागू न होकर अनेक टक्करों के सांख्यिकीय माध्य (statistical average) पर ही लागू होते हैं। अतएव आपाती विकिरण टामसन के तरंगवादी प्रतिरूप के अनुरूप सतत (continuously) प्रकीर्ण होता है, पर साथ में कभी-कभी एक प्रतिक्षेप (recoil) इलेक्ट्रान भी प्रकीर्णक से निकलता है। यह प्रतिरूप कांपटन परिणाम के कारण तरंगआयाम में वृद्धि का स्पष्टीकरण करने में सफल तो अवश्य हुआ, पर अंतत: कुछ प्रयोगिक परिणामों के आधार पर यह अमान्य हो गया और मान्यता, कांपटन एवं डेबाई के फ़ोटन-इलेक्ट्रान-टक्कर-प्रतिरूप को ही मिली।
कांपटन-डेबाई-प्रतिरूप के अनुसार प्रतिक्षिप्त इलेक्ट्रान और प्रकीर्ण विकिरण का उत्पादन साथ ही साथ होना आवश्यक है। इस युगपदीयता (Simultaneity) में क्वांटम यांत्रिकी के अनुसार समय अनिश्चिता (time uncertainty) लगभग १०-२१ सेंकड है और नवीनतम प्रयोगों में युगपदीयता समय इस सीमा के पर्याप्त निकट (फ़्१०-११सेंकड तक) पहुँच चुका है।
कांपटन-डेबाई के फ़ोटान प्रतिरूप में ऊर्जा और संवेग की स्थिरता का उपयोग करके प्रतिक्षिप्त इलेक्ट्रान और प्रकीर्ण फ़ोटान की दिशाओं में एक यथार्थ संबंध मिलता है। आधुनिक प्रयोगों से इस संबंध की संतोषजनक पुष्टि होती है।
डिरैक (Dirac) की क्वांटम यांत्रिकी (द्र. 'क्वांटम यांत्रिकी') के सिद्धांतों के अनुसार विद्युच्चुंबकीय क्षेत्र और एक इलेक्ट्रान के बीच अंत: क्रिया का स्पष्टीकरण पूर्णत: भिन्न रूप से किया गया है। इस प्रतिरूप में अंत: क्रिया की प्रारंभिक और अंतिम स्थितियों के अतिरिक्त एक मध्यम (intermediate) स्थिति भी होती है, जिसमें केवल संवेग ही स्थिर रहता है, ऊर्जा नहीं। इस अंत:स्थ स्थिति में एक इलेक्ट्रान एक फ़ोटान को उत्सारित (emit) कर सकता है या एक फ़ोटान का अवशोषण (absorption) कर सकता है। अत: कांपटन परिणाम में दो विकल्पों की शक्यता है :
(१) इलेकट्रान पहले आपाती फ़ोटान को प्रचूषित कर लेता है और अंत: स्थ स्थिति में कोई फ़ोटान उपस्थित नहीं रहता। अतिम स्थिति तक पहुँचने पर इलेक्ट्रान एक भिन्न ऊर्जा का (प्रकीर्ण) फ़ोटान उत्सारित कर देता है।
(२) इलेक्ट्रान पहले एक भिन्न ऊर्जा का (प्रकीर्ण) फ़ोटान उत्सारित कर देता है। अत: अंत:स्थ स्थिति में दो फ़ोटान उपस्थित रहते हैं। अंतिम स्थिति तक पहुँचने पर इलेक्ट्रान आपाती फ़ोटान का अवशोषण कर लेता है।
इन दोनों विकल्पों का विचार करके इलेक्ट्रान के विद्युच्चुंबकीय विकिरण के प्रकीर्णन का अध्ययन किया गया है और उससे जो निष्कर्ष निकले हैं (क्लाइन तथा निशीना के प्रकीर्णन क्रॉस सेक्शन के सूत्र) वे आधुनिक प्रयोगों द्वारा ऊर्जा के पर्याप्त विस्तार के लिए सिद्ध किए जा चुके हैं। कांपटन-डेबाई के निष्कर्ष इस सामान्य निष्कर्षों के विशेष रूप है। यदि प्रकीर्ण पदार्थ में हम इलेक्ट्रान की पूर्णतया स्वाधीन (अपरिबद्ध) और स्थिर मानें और यदि आपाती फ़ोटान की ऊर्जा प्ल आरू (hv�) हो और प्रकीर्ण फ़ोटान की ऊर्जा प्ल आव् (hv�) हो, तो ऊर्जा स्थिरता और संवेग स्थिरता के नियमों का उपयोग करके हमें निम्नलिखित समीकरण मिलते हैं :
प्ल आ० अ द्र० प्र२ उ प्ल आ
कोज्या त अ
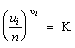 ...
. . . (१)
...
. . . (१)
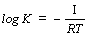 ...
(२)
...
(२)
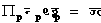 ...
(३)
...
(३)
जिनमें द्ररू (m� ) इलेक्ट्रान का स्थिर द्रव्यमान (rest mass) है, वे (उ ब प्र) अर्थात् द्व (उ ड ड़) प्रतिक्षिप्त इलेक्ट्रान का वेग है, त (f )
प्रतिक्षिप्त इलेक्ट्रान
ऊर्जा
उ m c2
उ ![]()
संवेग
उ m u उ![]()
�
प्रकीर्णन कोण है और थ (q) प्रतिक्षिप्त इलेक्ट्रान की दिशा और आपाती फ़ोटान की दिशा के बीच का कोण है।
इन मूल समीकरणों के उपयोग से हमें निम्नलिखित निष्कर्ष मिलते हैं :
कांपटन विचलन-
![]() .
. . (४)
.
. . (४)
विकीर्ण फ़ोटान की ऊर्जा-
प्ल आ
![]()
जिसमें
ण उ ![]()
प्रतिक्षिप्त इलेक्ट्रान की गतिज ऊर्जा-
ऊगतिज
उ प्ल आस् - प्लआव् ![]() ...
(६)
...
(६)
ऊगतिज उ प्ल आस्
![]()
ऊगतिज उ प्ल आस्
![]()
प्रकीर्णन कोणों त (f) और थ (q) का परस्पर संबंध निम्नांकित है
कोस्प था (१ अ ण) स्प ह त
[cot q उ (१ अ a) tan � f]
समीकरण (४) से आपाती फ़ोटान और प्रकीर्ण फ़ोटान के तरंगआयामों का अंतर, जिसे कांपटन विचलन (shift) कहते हैं, ज्ञात होता है। यह कांपटन विचलन केवल प्रकीर्णन कोण पर निर्भर रहता है, आपाती फ़ोटान की ऊर्जा पर बिलकुल नहीं।
क्लाइन-निशीना सूत्र–डीरैरक की क्वांटम यांत्रिकी के आधार पर क्लाइन और निशीना ने कांपटन परिणाम के लिए अवकल प्रकीर्णन अनुप्रस्थ काट (differntial sacatting cross-section)
ता (ई ढ), (es), ज्ञात किया, जिसकी परिभाषा हम
ता (ई ढ), [d(es)]= पुन: विकिरण शक्ति से कर सकते हैं
आपाती ऊर्जा
यदि हम आपाती विकिरण अनभिस्पंदित (unpolarized) लें और प्रकीर्ण फ़ोटान को प्रकीर्णन कोणों त (f) और तअतात (f + df) के बीच ठोस कोण ता ठो (ड्डज़्) से जाने दें तो क्लाइन और निशीना के अनुसार
ता (ईढ) उ ह गा०२ (आफ़/आ०)२ (आ०/आफ़ अ आ/आ० - ज्या२ त)
ता ठो सेंमी२
इलेक्ट्रान
![]()
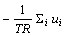
![]() d
W cm2/electron (१०)
d
W cm2/electron (१०)
जिसमें गा० � <2/p�0 |�2, y0 � e2/m0 c2
और ता ठो उ २ द्र ज्या त ता त (d W = 2 p sin f d f).
इसी समीकरण का अनुकलन (Intergration) करने पर हमें समस्त प्रकीर्णन अनुप्रस्थ काट (Total scattering cross-section) ज्ञात होता है :
ईढ उ द्र गा०२ लघु (१ अ २ ण)
लघु (१ अ २ ण)
![]()
![]()
![]()
![]()
![]() ...
...(११)
...
...(११)
समीकरण (१०) और (११) प्रयोगों द्वारा सत्यापित किए जा चुके हैं और इनकी सफलता डिरैक की इलेक्ट्रान थियरी की सत्यता का पहला प्रमाण है, क्योंकि दूसरे प्रमाण, पॉज़िट्रान का आविष्कार कई वर्षों के उपरांत हुआ।
परिबद्ध इलेक्ट्रानों से कांपटन प्रकीर्णन कांपटन तथा डेबाई और क्लाइन तथा निशीना के समीकरण इसी धारणा पर आधारित हैं कि इलेक्ट्रान प्रारंभ में अपरिबद्ध और स्थित हैं। यह धारणा केवल संयोजी (valence) इलेक्ट्रानों के लिए ही मान्य है पर अधिक बंधकारी ऊर्जा (binding energy) वाले इलेक्ट्रानों, जैसे के तथा एल (K or L shell) इलेक्ट्रानों के लिए मान्य नहीं है।
प्रयोगों से यह देखा गया है कि कांपटन प्रकीर्ण विकरण को यदि किसी एक प्रकीर्णन कोण पर मापा जाए तो उसका केवल एक तरंगआयाम नहीं मिलता, एक निश्चित विस्तार में तरंगआयाम मिलता है। यह तरंगआयाम का विस्तार (breadth) प्रकीर्णक के के–तथा एल (K तथा L) इलेक्ट्रानों के संवेग के कारण होता है।
परिबद्ध इलेक्ट्रानों और नाभिक के बीच जो बंधकारी ऊर्जा होती है उसके कारण अधिकतम संभावी कांपटन विचलन में कुछ त्रुटि क़्दे (D l) उत्पन्न हो जाती है जो बंधकारी ऊर्जा की अनुपाती होती है :
![]() .
. . (१२)
.
. . (१२)
और दै
![]() . . . (१३)
. . . (१३)
जहाँ दैव्व् (lव्व्) अधिकतम संभावी प्रकीर्ण तरंग आयाम है और ख (b) एक स्थिरांक है।
सं.ग्रं. ए.एच. कांपटन तथा एस. के. ऐलिसन : एक्स-रेज़ इन थियरी ऐंड एक्सपेरिमेंट (डी. वान नोस्ट्रैंड कं. न्यूयार्क, १९४८); आर.डी.एवांस : दि ऐटोमिक न्यूक्लियस (मैकग्रॉ हिल बुक कं., न्यूयार्क, १९५५); हांडबुख़ डर फ़िज़ीक, खंड ३४ (श्द्रिन्गर वरलाग, बर्लिन, १९५८)। (ज.सिं.)