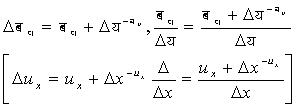
कलन (परमित अंतरों का) यदि कुछ राशियाँ परस्पर आश्रित हों तो उनकी युगपद् वृद्धियों के अनुपातों का अध्ययन जिस विज्ञान का विषय है, उसी का नाम परिमित अंतर कलन है। साधारणतया इसका उपयोग सांख्यिकी सिद्धांत और अवलोकन सिद्धांत में होता है। इसके विपरीत अवकल कलन में उन सीमाओं का अध्ययन किया जाता है जिनकी ओर उक्त अनुपात तब अग्रसर होते हैं जब वृद्धियाँ अत्यल्प हो जाती हैं।
वृद्धियों के लिए हम इस संकेतलिपि का प्रयोग करेंगे :
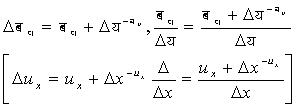
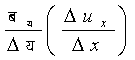एक
वास्तवकि भिन्न
है, किंतु अवकल
कलन की राशि
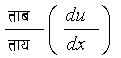कोई
वास्तवकि भिन्न
नहीं है, और न
ताब (dn)
और ताय (dx)
का एक दूसरे
से स्वतंत्र अस्तित्व
ही है।
यदि 
य
(x)
यदि को मान
१ दिया जाए,बय
बय+१
- बब (ux
= ux+1 - ux)
माना जाए, तो
तब य
= ट
(x
= h) तो
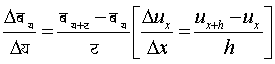
य (x) के किसी फलन के अंतरों के अंतर को द्वितीय अंतर कहते हैं। यथा
बय
= २बय, स-१
बय =
सबय
ux
=
2ux, n-1
ux =
nux
यदि बय उ य३ (ux = x3) तो हमें निम्नलिखित सारणी प्राप्त होगी : य के मान
1 2 3 4 5 6
[ values of x 1 2 3 4 5 6]
बय १ ८ २७ ६४ १२५ २१६
[ux 1 8 27 64 125 216]
बय ७ १९ ३७ ६१ ९१
[ux 7 19 37 61 91]
२बय १२ १८ २४ ३०
[2ux 12 18 24 30]
३बय ६ ६ ६
[3ux 6 6 6]
बय
= (य
+१)३
- य३ = ३
य२ +
३ य +
१, २बय
= (३
य२ +
य +
१) = ६ य
+ ६, ३बय
= ६
[ux
= (x + 1)3 - x3 = 3x2 + 3 x + 1] 2ux
= (3x2
+ 3 x + 1) = 6x + 6, 2ux
= 6]
यदि (ux) य (x) के स वें (nth,/-) घात का, कोई परिमेय, पूर्णांक फलन हो तो उसका स वाँ (n th) अंतर इस प्रकार निकलेगा :
बय = क यस + ख यस-१ अ . . . [ux = axn + bxn-1 + . . . ]
बय
= क (य
+ १)स
+ क
(य +
१)स-१ +
. . . - क यस
+ ख यस-१
अ . . .
[
ux
= a (x+I)n + b (x + I)n-1 +.
. . - axn - b xn-1 - . . .]
अर्थात् ब य उ क स यस-१ अ ख यस-२ अ ख२ यस-३अ . . .
[ux=
a nxn-1+
b xn-2 + b2xn-3 + . . .]
जिसमें
ख१, ख२,... (b1,
b2...) अचर हैं। अत:
बय
(ux)
(स - १) वें [(nI)th])
घात का फलन है।
अंत में, सबय
= क स (स—१)
(स—२)
. . . ३. २. १
[nu
= a n n—1) (n—2). . . 3. 2.1]
और सयस
= स!
[nxn = n !]
२. प्रारंभिक फलनों के अंतर
(१) यदि बय उ य (य—१) (य—२) ... (य—म +१)
[ux = x (x—1) (x—2)... (x—m + I)]
बय
= म
य (य—१)
(य—२)
... (य—म
+२)
[ux
= m x (x—I) (x—2)... (x—m + 2)]
इस संबंध में निम्नलिखित संकेतलिपि प्रयुक्त होती है, जिसका नाम क्रमगुणन संकेतलिपि है :
य (य–१) (य–२) ... (य–म अ१) = य (म)
[ x (x—I) (x—2)... (x—m + I) = x (m)]
हमें प्राप्त है :
य
(भ) म य (म-१)
[x
(m) = m x (m-1)]
अत:य
(न) उ म (म–१)
य (म-२) [2x
(m) = m (m—1)x (m-2)]
सय (म) उ म (म–१)... (म–स अ१) य (म-स)
[nx
(m) = m (m—1)... (m—n + 1)x (m-n)]
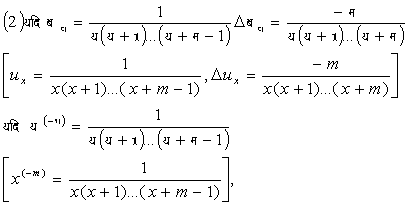
हमें प्राप्त
है य
(-भ) =
- म य (- भ-१) [x
(-m) = - m x (- m - 1)] उत्तरोत्तर
पदों से हमें प्राप्त
होगा
सय-भ
(न) =
(–१)भ
म (म +१)...
(म+स
-१) य (-भ -स)
[nx
(-m) = (—I)m m (m + I)... (m + n – I)x (-m -n)]
इसी प्रकार के और भी उदाहरण दिए जा सकते हैं।
(३) क्रमगुणितों में प्रसार
यदि फ (य) उ क अ ख य अ ग य(२) अ ट य (म)
[ f (x) = a + b x + cx(2) + ... h x (m)]
तो फ
(य) =
ख +
२ ग य +
३ घ य(२)+
...म ट य(म-१)
[f
(x) = b + 2 c x + 3 d x(2) + ... mhx (m-I)]
म
फ (य ) =
म (म –१)...
२. १. ट ।
[mf
(x) = m (m -I)... ... 2. I. h]
यदि हम इनमें से प्रत्येक में म = 0 (x = 0) रखों तो हमें प्राप्त होगा,
फ (0) = क, फ (0) = ख, D2फ (0) = 2ग, . . . Dम फ (0) = 1. 2. म ...ट।
[f
(0) = a,f
(0) = b, 2
f (0) = 2 c, ... . . . f
(0) = 1. 2. ... m h]
अत:
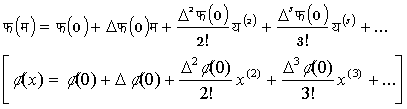
४. बय (ux) और अंतर श्रेणी के पदों में बमअस (ux+n) का प्रसार हमें हस्तगत है :
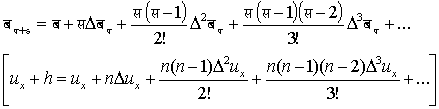
५. धा-संकेतलिपि ( E-notation)
धा बय स् बस्ा+1 [Eux º ux+1]
वितरणशील
है : (बय
अ भय अ...) बय
अ भय
[
(ux
+ ux +...) = ux
+ vx
+...]
किसी अचल गुणांक के प्रति व्यत्यशील है।
क
बय =
क बय
[aux
=a
ux]
धा =
१ + [E
= 1 + ]
बय+१ = धा बय [u+1 = E u]
बय+२ = धा२ बय [u+2 = E2 u]
बय+३
=
धाम बय =
(1
+ D)
बयम
[ux+n = En ux= (1 +)n
ux]
सं.ग्रं.—बूल : ट्रिटिज़ ऑन द कैलक्युलस ऑव फ़ाइनाइट डिफ़रेंसेज़। (ना.गो.श.)