के म (m) पदों का योगफल

य_म

यदि म (m) (अनंत की ओर प्रवृत्त हो तो य_म (S_m), स्वयं २ (२) की ओर प्रवृत्त होगा।

यदि यह सीमा विद्यमान हो।

यदि ऊपर दी हुई सीमा विद्यमान हो तो उसे

तार अथवा तार/ताय

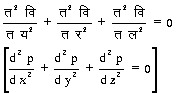
ताय

से प्रदर्शित करते हैं। इस चिह्न में अक्षर ता, य, र, ताय, तार, (d, x, y, dx, dy) का अलग-अलग कोई अर्थ नहीं है। पूरा तार/ताय ऊपर दी हुई सीमा का मान द्योतित करता है तथा र (y) का य (x) के सापेक्ष अवकलज कहलाता है। तार (dy) और ताय (dx) का केवल एक परिस्थिति में अलग-अलग अर्थ लिया जाता है, जिसको जानने के लिए कलन की विशिष्ट पुस्तकें द्रष्टव्य हैं। तार/ताय (dy/dx) साधारणत: अवकल गुणांक कहलाता है। अवकलज ज्ञात करने की क्रिया को अवकलन करना या अवकल ज्ञात करना कहते हैं। जैसे, मान लें र उ य^म [y = e ^m],तो अवकल गुणांक

के और उच्च घात }

इसी प्रकार यदि र ज्या य (y = sin x),

तो कोज्या य

तथा र उ क , ता

अवकल गुणांक ज्ञात करने की अनेक विधियाँ अवकल कलन की पुस्तकों में दी रहती हैं जिनसे किसी फलन का अवकल गुणांक सुगमता से ज्ञात हो सकता है। गणित में अवकल गुणांक बहुत उपयोगी है। विज्ञान की अन्य शाखाओं में भी इसका अधिकाधिक प्रयोग हो रहा है। सच पूछिए तो आधुनिक युग के विज्ञान की उन्नति कुछ सीमा तक कलन पर ही निर्भर है। इसका प्रयोग वक्रों के स्पर्शी, उनके महत्तम अल्पतम बिंदु, उनकी वक्रता, अवगुंठन (एनवेलप, enveloper) इत्यादि तथा परिवर्तनशील राशियों की तात्कालिक परिवर्तन दर तथा उनके पारस्परिक संबंध इत्यादि निकालने में होता है।

स्पर्शी अवकल गुणांक का अर्थ वक्र के स्पर्शी से सुगमता से विकसित हो सकता है। मान लें आसन्न चित्र वक्र र = फ (य) [y = f (x)] का रेखाचित्र है। वक्र पर ब (P) कोई बिंदु है। म (Q) काई अन्य बिंदु है। रेखा बम (PQ) खींचें। इसे बिंदु ब (P) पर इस प्रकार घुमाएँ कि बिंदु म (Q) बिंदु ब (घ्) की ओर आए और मब (PQ) को इतना घुमाएँ कि बिंदु म (P) बिंदु प (P) पर पहुँच जाए; तो छेदन रेखा ब म (PQ) की सीमा बिंदु ब (P) पर की स्पर्शी होगी।

�

�

यहाँ या (X) और रा (ज््ञ) नियामक है।

यदि बिंदु म (Q) बिंदु ब (P) की ओर अग्रेसारित हो तो इस समीकरण का रूप निम्नलिखित होगा:

क्योंकि

अपनी चरम सीमा में

हो जाएगी अर्थात् तार उस कोण की स्पर्शज्या है जो कि उस बिंदु पर की स्पर्शी य-अक्ष के साथ बनाती है। इस कोण को जानकर स्पर्शी आसानी से खींची जा सकती है। मान लें, परवलय

४ र = य^२ [4 y = x²]

के बिंदु (२, १) पर स्पर्शी खींचना है तो यहाँ ह य [dy/dx उ ह न्ट जिसका मान दिए बिंदु पर १ हे। अब बिंदु (२,१) से ऐसी रेखा खींचें जिसकी प्रवणता १ हो। यही उस बिंदु पर परवलय की स्पर्शी है।

परिवर्तन दर किसी परिवर्तनशील राशि की तात्कालिक परिवर्तन दर से विवेचन से भी अवकलज का भाव विकसित किया जा सकता है। मान लें कोई गण बिंदु का (ॠ) से चलना प्रारंभ करता है और उसका वेग प्रतिक्षण बढ़ता रहता है, तो प्रश्न उठता है कि पथ के किसी बिंदु खा (ए) पर कण का वेग कैसे नापा जाए।

का (A) खा (B) गा (C)

यदि कण समान वेग से चलता तो बिंदु खा (B) से किसी अन्य बिंदु गा (C) तक जाने का समय नाप लेते तथा दूरी खा गा (BC) को उससे भाग देकर कण का वेग निकाल लेते। पथ के प्रत्येक बिंदु पर कण का वेग समान होता तो ऐसा किया जा सकता है था, परंतु कण का वेग हमारे प्रश्न में प्रत्येक बिंदु पर भिन्न है। यदि बिंदु का (A) से खा B) की दूरी द (s) तथा खा (B) से गा (C) की दूरी दव् (d) हो तथा का (A) से खा (B) तक चलने का समय स (t) हो तो दव्/सव् (s�/t�) बिंदु खा (B) से गा (C) तक का मध्यमान (औसत) वेग होगा। यह बिंदु खा (B) पर के वेग से अधिक तथा गा (C) पर के वेग से कम होगा। यदि हम समय सव् (t�) अत्यंत अल्प रखें तो भी खा (B) बिंदु पर का वेग ठीक ज्ञात नहीं हो सकता। दव्/सव् (s�/t�) उसका केवल लगभग मान ही बतलाएगा। ठीक-ठीक मान जब तक ज्ञात नहीं हो सकता जब तक समय सव् (t�) के बराबर न हो जाए। परंतु सव् (t�) शून्य करते ही दव् (s�) भी शून्य हो जाता है। और इसलिए दव्/सव् [s�/t�] का मान निकल ही नहीं सकता। इस कठिनाई से बचने के लिए वेग की परिभाषा यों दी जाती है :

कण का बिंदु खा (B) पर वेग

यह स्पष्ट है कि समय स (द्य) में चली हुई दूरी स (t) के मान पर निर्भर है, अर्थात् स (t) का एक फलन है, अर्थात् द फ (स) [S = f (t)] , जिससे ताद/तास्ा [ds/dt] का मान किसी भी समय स (द्य) पर कण के वेग का मान होगा। इसी प्रकार यदि समय स (द्य) पर कण का वेग व (v) हो तो

त्वरण

महत्तम अल्पतम मान किसी वक्र प = फ [y = f (x)] के रेखाचित्र पर विचार करें :

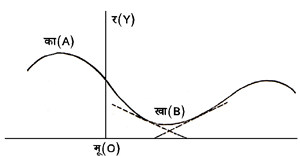
इस चित्र के बिंदु का (A), गा (C) राशि र (p) के महत्तम मान प्रदर्शित करते हैं और खा (B) अल्पमत मान। बिंदु का (A) और गा (C) पर वक्र का ऊपर उठना रुक जाता है और नीचे उतरना आरंभ हो जाता है। बिंदु खा (B) पर इसके विपरीत उतरना रुक जाता है और ऊपर उठना प्रारंभ हो जाता है। ज्यों-ज्यों वक्र ऊपर उठता है त्यों-त्यों स्पर्शी की प्रवणता (अर्थात् स्पर्शी और य(x) अक्ष के बीच के कोण की स्पर्शज्या, जिसका मान तार/ताय [dy/dx] है), घटती जाती है और नीचे उतरने पर बढ़ती जाती है। क्योंकि ऊपर उठते समय स्पर्शी और य(x) अक्ष के बीच का कोण न्यून कोण है, अत: इसकी स्पर्शज्या अर्थात् तार/ताय [dy/dx] का मान धन होगा और उतरते समय वह कोण अधिक कोण होगा अर्थात् तार/ताय [dy/dx] ऋण होगा। अत: बिंदु का और गा पर तार/ताय [dy/dx] का मान धन से ऋण की ओर जाएगा। इस क्रिया में वह स्थान पर अवश्य शून्य के बराबर होगा। वही स्थान महत्तम बिंदु होगा। इसी प्रकार खा पर तार/ताय [dy/dx] का मान ऋण से धन में बदल जाएगा अर्थात् उस बिंदु पर उसका मान शून्य होगा। अत: महत्तम और अल्पतम बिंदुओं पर

इस संबंध से उन बिदुओं का पता लगाया जा सकता है। उदहारण : एक छड़ २० फुट लंबी है, उसका ऐसा आयत बनाएँ जिसका क्षेत्रफल महत्तम हो।

मान लें आयत की एक भुजा य (न्) है, तो दूसरी २०-य (२०-न्) होगी और उसका क्षेत्रफल

र उ य (२०- य) उ २० य - य^२ [y = x (20—x) = 20xx²]

महत्तम के लिए

तार/ताय = 20-2य = 0 [dy/dx = 20-2x = 0]

अत: य =10 [x = 10];

अर्थात् जब छड़ वर्ग के लिए रूप में होगा तब क्षेत्रफल अधिकतम होगा।

अवकलज के अन्य प्रयोग अवकल कलन की पुस्तकों में मिलेंगे।

अनुकल किसी दिए हुए फलन के अनुकल के दो मुख्य अर्थ होते हैं। एक तो ऐसा फलन जिसका अवकलज वह दिया फलन हो और दूसरा, एक विशेष श्रेणी के पदों के योग की सीमा। इस दशा में वह सीमित अनुकल कहलाता है।

यदि एक फलन दूसरे फलन का अलकल गुणांक हो तो दूसरा फलन पहले का अनुकल कहलाता है। जैसे ऊपर बताया जा चुका है कि य^म (न्^्थ्र) का अवकल गुणांक मय^म-१ है; अत: य^म (x^m) फलन म य^म-१ [m x^m-1] का एक अनुकल है। एक अनुकल इसलिए कहा जाता है कि यदि य^म अ क, [x^m + c] का अवकलज निकालें तो वह भी म य^म-१ [m x^m-1ट ही होगा। अत: य^म अ क, [x^m + c] फलन म य^म-1 [m x^m-1] का पूर्ण अनुकल है, जिसका य^म (x^m) एक विशेष रूप है। इस विचार को

से प्रदर्शित करते हैं और पहले को 'अनुकल म य^म-१ ताय बराबर है के य^म अ क'' के पढ़ते हैं।

सीमित अनुकल माने लें फ (य) [f (x)] स्वतंत्र चर य (न्) का कोई फलन है, जिसका अंतराल क, ख [a, b] में प्रत्येक बिंदु पर केवल एक मान है। मान लें, चित्र में मूका उ क, मूखा उ ख [OA = a, OB = b] ।

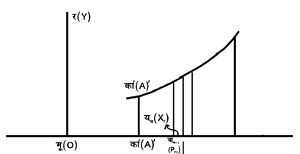
अंतराल को बिंदु बा_१ (P₁), बा_२ (P₂), . . .बा_म-१ [P_m-1] म (m) भागों में बाँटो। यहाँ

मूका < मूबा_१ < मूबा_२ < . . . < मूबा_च < मूबा_S�+1 < . . . < मूखा

[OA < OP₁ < OP₂ < . . . < OP_r <OP_{r + 1} < . . . < OB]

फ (य) ताय

यदि फ (य) तो

फ (य) ताय उ फा (ख) - फा (क)

इस प्रमेय द्वारा सीमित अनुकल का मान ज्ञात होता है।

निश्चिम समाकल बहुत उपयोगी है। इसका एक प्रयोग है क्षेत्रफल निकालना, जिसका उदाहरण नीचे दिया हुआ है।

मान लें कि आसन्न चित्र वक्र र = फ [y = f (x)] का रेखाचित्र है

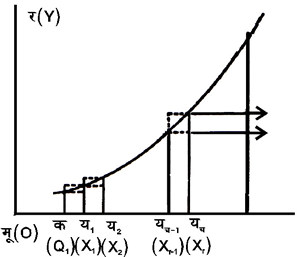
रेखाएँ य = क तथा य = ख खींची गई हैं, जो वक्र बिंदुओं का और खा पर काटती हैं। तो क्षेत्र क ख खा का का क्षेत्रफल

फ (य) ताय

है। अंतराल क (a), ख (b) को म (m) भागों में बाँटें। प्रत्येक विभाजक बिंदु य_१, य_२, . . . (x₁, x₂, . . .) से र - (y-) अक्ष के समांतर रेखाएँ खींचें जो वक्र को या_१, या_२ . . . (X₁, X₁. . .) पर काटें। या_१, या_२ . . . (X₁, X₁. . .) य - (x-) अक्ष के समांतर रेखाएँ खींचें। तो प्रत्येक अंतराल, जैसे य_च-१, य_च (x_r-1, x_r ) पर दो आयत बनेंगे जिनमें से स्पष्टतया एक क्षेत्र य_च-१, य_च या_च या_च-१, (x_r-1, x_{r ,} X_r, X_r-1) से छोटा और दूसरा पड़ा होगा, अर्थात्

[Rect. x'_r-1 X'_r < Area _r-1 x_r X_r X_r-1 < Rect x_r-1 X]

जिन आयताकार क्षेत्रों में क्षेत्रफल क ख खा का रेखाओं य उ य, य उ य,. . . (x = x₁, x = x₂ . . . ) से विभाजित है उन सबके लिए ऐसी ही असमानताएँ लिखकर जोड़ने से

अत: क्षेत्र क ख खा का (a b B A) का क्षेत्रफल भी

इसी प्रकार पिंडों के आयतन, पृष्ठों के क्षेत्रफल और वक्रों की लंबाई इत्यादि का मान निकालते हैं।

(झ.ला.श.)