उष्मामिति किसी रीति से उष्मा के मापन को उष्मामिति कहते हैं। उष्मामिति उष्मा के किसी प्रभाव पर आधारित होती है। उष्मामापन की साधारणतया निम्नलिखित पद्धतियाँ हैं :
(क) तापपरिवर्तन अथवा तापमानीय उष्मामिति,
(ख) अवस्थापरिवर्तन अथवा गुप्त ताप उष्मामिति।
प्रथम पद्धति में वे रीतियाँ हैं जिनमें ताप परिवर्तित होता है तथा मापन तापपरिवर्तन पर निर्भर होता है। अंतत: यह पद्धति केवल ताप के अवलोकन में परिणत हो जाती है। अत: इन विधियों में तापमान के अवलोकन में परिणत हो जाती है। अत: इन विधियों में तापमान एक मुख्य उपकरण है। इस पद्धति में रेनो की मिश्रण विधि तथा ड्यूलाँग और पेती की शीतलीभवन विधि हैं।
दूसरी पद्धति में वे विधियाँ सम्मिलित हैं जो ठोसों के द्रवण अथवा वाष्पों के संघनन पर निर्भर हैं। इनमें हिम तथा वाष्प उष्मा मान सम्मिलित हैं। द्रवण तथा वाष्पीकरण पर निर्भर होने के कारण इन प्रयोगों में ताप स्थिर रहता है, अतएव इनमें तापमापन की कोई आव 40;ा नहीं होती।
(क) ताप-परिवर्तन-उष्मामिति में जल का तापन एक नियत ताप तक किया जाता है तथा इस जल की मात्रा से उष्मा की मात्रा ज्ञात की जाती है।
उष्मा का एकक-उषमा का एकक उष्मा की वह मात्रा है जो एक एकक मात्रा जल के ताप में १� श्की वृद्धि करती है। यदि द्रव्यमान का एकक १ ग्राम हो तो तथा तापांतर १� सें. हो तो उष्मा के एकक को एक कलरी कहते हैं। १ ग्राम द्रव्यमान के जल के ताप में १� श्सें. वृद्धि करने के लिए प्रत्येक ताप पर उष्मा की आवश्यक मात्रा समान नहीं होती। अत: वैज्ञानिकों ने १� श्सें. का पूर्वोंक्त तापंतर १४.५� श्सें से १५.५� श्सें. तक माना है। अत: एक कलरी उष्मा की वह मात्रा है जो १४.५� श्सें. के एक ग्राम जल के ताप को बढ़ाकर १५.५� श्सें. कर दे। विभिन्न तापों पर एक डिगरी ताप बढ़ाने के लिए आवश्यक उष्मा की मात्रा में अंतर बहुत कम हाता है; अत: साधारण प्रयोगों में किसी भी ताप पर १ ग्राम शुद्ध जल के ताप में १� श्सें. की वृद्धि के लिए आवश्यक उष्मा की मात्रा को १ कलरी मान सकते हैं।
अंग्रेजी पद्धति में १ पाउंड शुद्ध जल के ताप में १� श्फारेनहाइट वृद्धि के लिए आवश्यक उष्मा को उष्मा का एकक माना गया है। इसके उष्मा का अंग्रेजी एकक (ब्रिटिश थर्मल यूनिट : बी. टी-एच.यू.) कहते हैं।
१ पाउंड = ४५३.६ ग्राम तथा १� श्फा. = ४/९� श्सें.।
अत: १ ब्रिटिश थर्मल यूनिट = ४५३.६ �४/९
=२५२ कैलरी
उष्माधारिता-किसी वस्तु की उष्माधारिता उष्मा की वह मात्र है जो १ सें. तापवृद्धि के लिए उस वस्तु को देनी पड़ती है, अथवा १ सें. तापपतन द्वारा उससे प्राप्त होती है।
विशिष्ट उष्मा-जल की उष्माधारिता की तुलना में किसी पदार्थ की उष्माधारिता को उस पदार्थ की विशिष्ट उष्मा कहते हैं। अर्थात्, पदार्थ के किसी द्रव्यमान की किसी तापवृद्धि के लिए आवश्यक उष्मा की मात्रा तथा समान द्रव्यमान के जल की उसी तापवृद्धि के लिए आवश्यक उष्मा की निष्पत्ति को उस पदार्थ की विशिष्ट उष्मा कहते हैं। १ ग्राम जल की १� सें. तापवृद्धि के लिए आवश्यक उषमा १ एकक उष्मा होती है अत: एक ग्राम पदार्थ की उष्माधारिता उस पदार्थ की विशिष्ट उष्मा होती है, यदि द्रव्यमान द्र (m) की किसी वस्तु का ताप थ� (q�) से था� (q�) तक बढ़ाने के लिए आवश्यक उष्मा की मात्रा मा (Q) हो तो पूर्वोक्त परिभाषा के अनुसार विशिष्ट उष्मा वि (S ) निम्नलिखित सूत्र में प्राप्त होगी
���������������������������������������������������������������������� (1)
����������������������� 
�������������������������������������������������������������������������������� (I)
इसमें वि (S ) ताप थ (q) तथा था (q�) के बीच मध्यक उष्मा है। किसी तापश् थ (q) पर विशिष्ट उष्मा ज्ञात करने के लिएश् था (q�) कोश् थ (q) के अति निकट लिया जाता है, अत: था - था (q�-q) के स्थान पर ताथ (d q) तथा तत्संबद्ध उष्मा की मात्रा तामा (d Q)श् मानकर
����������������������������������������������������������������������������� (1)
����������������������� 
���������������������������������������������������������������������������������� (2)
इससे यह सिद्ध हुआ कि किसी वस्तु की उष्माधारिता उस वस्तु के द्रव्यमान तथा विशिष्ट उष्मा का गुणनफल है। इसे उस वस्तु का जल तुल्यांक भी कहते हैं।
गैसों की
विशिष्ट उष्मा-साधारणतया
विशिष्ट उष्मा की परिभाषा करते समय उस परिस्थितियों का
निर्देशन आवश्यक है जिनमें तापपरिवर्तन हुआ हो।
उदाहरणतया, यदि संपीडन से किसी गैस के ताप में वृद्धि हो
तो ताथ �
(dq �) , परंतु तामा
= ० (dQ =)। अतएव
विशिष्ट उष्मा वि (S) शून्य होगी।
पुन: यदि एक गैस में परिमित मात्रा में उष्मा दी जाए और उसका
प्रसरण इस प्रकार हो कि उसका ताप स्थिर रहे तो इस
परिस्थिति में ताथ = ० (dq =) तथा तामा = ० श्(dQ =)। अतएव
विशिष्ट उष्मा अत्युच्च होगी। गैस का प्रसरण इस प्रकार भी
कराया जा सकता है कि कुछ मात्रा में उष्मा तो उसे दी जाए परंतु
फिर भी उसके ताप का पतन हो; तब ताथ (dq )
के ऋण होने के कारण उसकी विशिष्ट उष्मा का मान भी ऋण होगा।
इससे यह प्रतीत होता है कि गैस की विशिष्ट उष्मा का मान + � श्से - � के अंतर्गत कुछ भी हो
सकता है तथा यह मान परिस्थितियों से संबंधित है। इस
कारण गैस की विशिष्ट उष्मा के विषय में तापपरिवर्तन की
परिस्थितियों का निर्देशन अत्यंत आवश्यक है। अत: गैस के विषय
में दो विशिष्ट उष्माएँ होती हैं : (१) स्थिर दाब विशिष्ट उष्मा, विदा
(Cp) तथा (२) स्थिर आयतन
विशिष्ट उष्मा, विआ (CV)।
द्रव तथा ठोस पदार्थों में संपीडन न्यून होने के कारण साधारण प्रयोगों में आयतन परिवर्तन न्यून तथा नगण्य होते हैं। अत: एक ही विशिष्ट उष्मा रह जाती है। प्रत्येक ताप ताप पर ठोस तथा द्रव की एक निश्चित विशिष्ट उष्मा होती है तथा ताप के साथ इसकी वृद्धि होती है।
तापपरिवर्तन उष्मामिति-इस पद्धति में निम्नलिखित रीतियाँ हैं :
(क) मिश्रण विधि,
(ख) शीतलीभवन विधि।
(क) मिश्रण विधि द्वारा रेना ने परम शुद्ध फल ज्ञात किए।
यदि दो पदार्थ क तथा ख के द्रव्यमान द्र१ (m1) तथा द्र२, (m2) ताप थ१ श्(q1) तथा थ२ श्(q2) तथा विशिष्ट उष्माएँ वि१ (S1) तथा वि२ (S2) हों और यदि वे एक दूसरे के साथ रखे जाएँ तो उष्मा एक से दूसरे में जाएगी तथा फलस्वरूपश् थ१ तथा थ२ के अंत:स्थ एक सामान्य ताप थ (q) होगा। परिणामत: यदि उष्मा का नियमन क तथा ख ही में हो तो क द्वारा दी गई उष्मा ख द्वारा ली गई उष्मा के तुल्य होगी-
अत: द्र१ वि१ (थ१- थ) = द्र२ दि२ ((थ - थ२) . . . (३)
m1 S1 (q1-q) = m2� S2 (q1-2)�������������������������������� . . . (३)
अब यदि क जल की कोई मात्रा है तो परिभाषानुसार वि२ (S2) का मान १ होगा तथा ख की विशिष्ट उष्मा निम्नलिखित समीकरण से ज्ञात होगी :
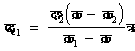��������������������������������������������������������������� . . . (४)
���������������������������������������������������������� . . . (४)
यहाँ वि१ (S1) ताप थ (q) तथा थ१ (q1) के अंतर्गत मध्यक उष्मा है। यहाँ हमने यह माना है कि ताप के समीकरण की अवधि में क तथा ख न तो अन्य वस्तुओं से उष्मा लेते हैं, न उन्हें देते हैं। व्यवहार में हय अवस्था असंभव है। सामान्यतया अन्य वस्तुओं से उष्मा का नियमन होता है। ऐसी त्रुटियों को दूर करने अथवा कम करने की विशेष रीतियाँ हैं।
उष्मामापी-उष्मामापन के प्रयोगों का मुख्य उपकरण ताँबे, पीतल अथवाचाँदी की पतली चद्दर का बना उष्मामापी होता है। यह एक बड़े बर्तन के भीतर कुचालक आधारों पर रखा जाता है। उषमामापी में मापे हुए द्रव्यमान का जल भरा होता है, जिसमें निश्चित ताप की तप्त वस्तु डाली जाती है तथा एक सूक्ष्म तापमापी से तापपरिवर्तन पढ़ा जाता है। जल को (दूर अथवा कम) चलाने के लिये उसमें ताँबे का मुड़ा हुआ विचालक रहता है। विकिरण द्वारा उष्मा का क्षय दूर अथवा कम करने के लिए उष्मामापी के बाहरी तल तथा बड़े बर्तन के भीतरी तल पर पालिश की जाती है।
किसी तप्त पदार्थ को उष्मामापी के जल में डालने पर जल के अतिरिक्त उष्मामापी, विचालक तथा तापमापी का पारा भी तप्त पदार्थ की उष्मा लेते हैं तथा उनके ताप में भी वृद्धि होती है। अत: इनकी उष्माधारिताओं का लेखा लेना भी आवश्यक है। यदि उष्मामापी का द्रव्यमान द्र१ (m1) ग्राम हो तथा विशिष्ट उष्मा वि१ (S1) हो तो उसकी १� सें. तापवृद्धि के हेतु द्र१ वि१ (m1 S1) कैलरी की आवश्यकता होगी।श् द्र१ वि१ (m1 S1) को उष्मामापी को जलतुल्यांक कहते हैं; क्योंकि द्र१ वि१ (m1 S1) ग्राम जल के ताप में भी १� सें. की वृद्धि होगी। अब यदि द्र१ द्र२ द्र३ (m1 m2 m3) ग्राम उष्मामापी, तापमापी का पारा तथा विचालक के द्रव्यमान हों तथा वि१' वि२' वि३ (S1' S2'� S3), उनकी विशिष्ट उष्माएँ, तो उष्मामापी तथा उपसाधनों का जलतुल्यांक ज (w) निम्नलिखित समीकरण से मिलेगा।
ज = द्र१ वि१ + द्र२ वि२ + द्र३ वि३ . . . (५)
W = m1 S1 + m2 S2� + m3� S3����������������������������������������������������������������������� . . . (५)
पारे की संहति द्र२ अति न्यून होती है तथा यदि विचालक और उष्मामापी एक ही धातु के बने हो तो
ज = द्र१ +श् द्र३ वि१
W = (m1 + m3 ) S1श्
अतएव समीकरण (३) निम्नलिखित होगा :
द्र१ वि१ (थ१ - थ ) = (द्र२ - ज ) (थ - थ२) + क्ष . . . (६)
m1 �S1 (q1-q) = (m2 +� W) (q-q2) + R������������������������������ . . . (६)
इसमें क्ष �(R) विकिरण तथा निकालने के लिए संदर्भ ग्रंथों में से किसी एक को देखिए।
यदि उष्माक्षय
के शोधन के कारण तापवृद्धि
थ हो तो
द्र१
वि१ {थ१� (- थ )} = (द्र२ + ज ) (थ + थ१ - थ२) ������� . . . (७)
m1 �S1
q - {q +q } = (m2 +�
W) (q
+ q1 - q2) �������� . . . (७)
तापांतर की वृद्धि से विकिरण शोधन में भी वृद्धि होती है; इस कारण उचित यह है कि उष्मामापी में जल की मात्रा इतनी अधिक ली जाए कि ताप में अधिक वृद्धि न हो; परंतु ऐसा करने से प्रयोग की सूक्ष्मता घट जाती है। इसके प्रतिकार के लिए सूक्ष्म तापमापी का व्यवहार आवश्यक हो जाता है।
(ख) शीतलीभवन विधि-इस कल्पना पर निर्धारित है कि जब कोई वस्तु किसी समावृत्त में शीतल होती है तो समय की अवधि ता स में उसके द्वारा उत्साहित उष्मा ता मा (dQ) (१) वस्तु के समावृत्त पर, (२) ताप के आधिक्य पर, (३) उसके तल की प्रकृति पर, तथा (४) तल के क्षेत्रफल पर निर्भर करती है। अत:
तामा = क. फ (थ). तास .श् . . (८)
dQ = A f (q) �dt������������������������������������������������������������ .श् . . (८)
इस समीकरण में क (A) वस्तु के तल पर, अर्थात् उसके क्षेत्रफल तथा विकिरण शक्ति पर निर्भर है, तथा फ (थ) श्[f (q)] ताप के आधिक्य का अज्ञात फलन है जो प्रत्येक वस्तु के लिए सम होगा। अत: यदि न्यूटन का शीतलीभवन नियम यर्थात है तो यह फलन केवल तापंतर थ (q) है। यदि तास (dt) अवधि में वस्तु तापांतराल ताथ (dq) से शीतल होती है तो
तामा = द्रवि ताथ। . . . (९)
dQ = m S d q����������������������������������������������������������������� . . . (९)
द्र (m) वस्तु की संहति तथा वि (S) विशिष्ट उष्मा है। अत:
द्र वि ताथ = क फ (थ) तास . . . (१०)
�m S dq = A f (q) �dt���������������������������������������������������� . . . (१०)
अतएव तापांतर थ१ �(q1) से थ२ �(q2) तक शीतल होने का समय स (t) निम्नलिखित होगा :
यदि एक अन्य वस्तु का द्रव्मान द्र� (m�) हो तथा विशिष्ट उष्मा वि� (S�) हो तो एक ही समावृत्त में तथा समताप प्रसार के लिए उसके शीतल होने का समय
���������������������������������� 
अतएव 
यदि दोनों वस्तुओं के तल के क्षेत्रफल समान हों तो क = क' (A=A') तथा
��������������������������������������������������������������������������������� (११)
�������������������������������������������������������������������������������������� (११)
अर्थात् दोनों वस्तुओं की उष्माधारिताएँ उन अवधियों की निष्पत्ति हैं जो उन वस्तुओं को ताप के समान परास (रेंज) द्वारा शीतल होने में लगती हैं।
यदि द्र१ (m1) तथा द्र२ (m2) द्रव्यमान के दो द्रव पदार्थ क्रमश: उष्माधारिता ज (W) के उष्मामापी में रखे जाएँ तथा यह उष्मामापी ० सें ताप के एक बर्तन के मध्य लटकाया जाए और तब शीतलीभवन की दर का अवलोकन किया जाए तो
(१२)
���������������������������������� 
������������������������������������������������������������������������� (१२)
यदि इनमें एक द्रव जल हो तो दूसरे द्रव की विशिष्ट उष्मा का मान ज्ञात किया जा सकता है।
इस रीति से परिशुद्ध फल नहीं मिलते। इसका केवल ऐतिहासिक महत्व ही रह गया है।
अवस्थापरिवर्तन अथवा गुप्त ताप उष्मामिति : (क) हिम-द्रवण विधि-ब्लैक ने प्रथम बार इस विधि का प्रयोग किया। हिम के एक बड़े टुकड़े में छोटा सा छेद बनाकर उसमे मुख को हिम के छोटे टुकड़े से बंद किया जाता है। इस प्रकार एक हिम से घिरा हुआ मंडल बन जाता है। ज्ञात द्रव्यमान की वस्तु को एक निश्चित ताप तप्त कर तथा हिममंडल के जल को सावधानी से सोखकर तप्त वस्तु को उसके भीतर तुरंत डाल दिया जाता है और उसके मुख को लघु हिम खंड से ढक दिया जाता है। यह वस्तु उष्मा देकर तुरंत हिम के द्रबांक पर आ जाती है तथा इससे निश्चित मात्रा में हिम का द्रवण होता है। पूर्व तौले हुए एक स्पंज से इस जल को सोखकर स्पंज को पुन: तौल लेते हैं तथा द्रवित हिम का द्रव्यमान ज्ञात कर लेते हैं। यदि वस्तु का आरंभिक ताप थश् (q ) , तथा द्रव्यमान द्र (m) तथा विशिष्ट उष्मा वि (S) हो तो उसे द्वारा दी हुई उष्मा की मात्रा द्र वि थ (m S q ) होगी। परिणामत:
द्र वि था = गु द्रा
m S q �= L W
यहाँ गु (L) हिमद्रवण की गुप्त उष्मा तथा द्रा (W) द्रवित हिम का द्रव्ममान है।
बुन्सेन का हिम-उष्मामापी-हिमद्रवण से आयतन का ्ह्रास होता है। इस सिद्धांत पर आधारित बुन्सेन का हिम उष्मामापी द्रवों तथा ठोस पदार्थों की विशिष्ट उष्मा ज्ञात करने का एक अत्यंत सुग्राही उपकरण है। यदि पदार्थ कम मात्रा में उपलब्ध हो तब भी उसकी विशिष्ट उष्मा ज्ञात की जा सकती है (द्र. चित्र २)।
संपूर्ण उपकरण के चारों ओर शुद्ध हिम भर देते हैं। नली क में कुछ शुद्ध जल रखते हैं। जब संपूर्ण उपकरण ०� सें ताप पर हो जाता है तो दिए हुए ठोस पदार्थ को एक स्थिर ताप ता� (T�) सें. तक तप्त करके तुरंत नली क के जल में डाल देते हैं। यदि ठोस का द्रव्यमान तथा विशिष्ट उष्मा क्रमानुसार उष्मा क्रमानुसार द्रा (M) तथा वी (s) हों तो ०� सें. तक शीतल होने में वह दा वी ता (M s T)श् कैलरी उष्मा देगा जिससे उस नली के चारों ओर के कुछ हिम का द्रवण होगा। अत: केशनली का पारा भीतर की ओर चलेगा। इसके पाठ से आयतन्ह्रास ज्ञात हो जाएगा। माना कि यह ्ह्रास आ (v)श् घन सें.मी. है। यदि हिम का विशिष्ट घनत्व घ (d) हो तो १ ग्राम हिम के द्रवण से आयतन में १/घ-१ [1/d-1] घ. सें.मी. की कमी होगी। माना कि यह य (x) है। अत: द्रवित हिम का द्रव्यमान आ/य (v/x) ग्राम। यदि हिम द्रवण की गुप्त की गुप्त उष्मा गु (L) हो तो
द्रा वी ता = (आ/य) गु। . . . (१३)
M s T = (v/x) L������������������������������������������������������������� . . . (१३)
इस उपकरण को उपयोग में लाने के लिए बहुत सावधानी की आवश्यकता होती है। इसमें जो पारा तथा जल रहता है उनक शुद्ध तथा वायुरहित होना अति आवश्यक है। बाहर के हिम का भी शुद्ध होना आवश्यक है।
श्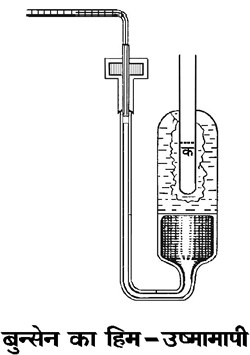
श्
चित्र २. बुन्सेन का हिम-उष्मामापी
(ख) वाष्पीकरण विधि-इस विधि में पदार्थ को एक मंडल में तुला के पलड़े पर रखकर उसमें १००� ताप का जलवाष्प तब तक भरते रहते हैं जब तक उस पलड़े की तौल स्थिर न हो जाए। दोनों तौलों के अंतर से संघनित वाष्प की मात्रा ज्ञात हो जाती है। यदि पदार्थ का द्रव्यमान, ताप तथा विशिष्ट उष्मा द्र (m), थ (q) तथा वि (S) हों, संघनित वाष्प का द्रव्यमान द्रा (M) और जलवाष्प की गुप्त उष्मा गु हो तो
द्रवि (१०० थ) = द्रा गु।
m s (100 - q)= M L
इसके लिए जॉली के जलवाष्प उष्मामापी का उपयोग होता है।
श्
श्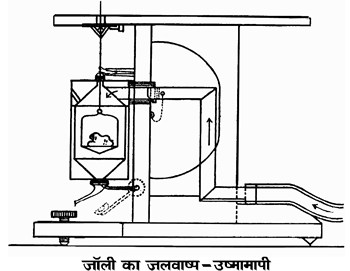
चित्र २. जॉली का जलवाष्प-उष्मामापी।
गैसों की विशिष्ट उष्मा-गैस की स्थिर आयतन विशिष्ट उष्मा का मान जॉली के विभिन्नक जलवाष्प उष्मामापी से ज्ञात किया जाता है। यह जलवाष्प उष्मामापी से कुछ भिन्न होता है। तुला की भुजा से धातु के एक सूक्ष्म तार द्वारा शुद्ध तथा शुष्क गैस से भरा हुआ एक गोला (बल्ब) लटकाया जाता है तथा दूसरी भुजा से इसके समरूप दूसरा गोला, जिसे निर्वात कर दिया जाता है। ये दोनों गोले एक ही मंडल में रहते हैं। अब पहले बताई गई रीति से गैस की विशिष्ट उष्मा ज्ञात की जाती है। (ब्योरे के लिए द्र. प्रेस्टन की पुस्तक)।
स्थिर चाप विशिष्ट उष्मा का मान ज्ञात करने के लिए रेनो के उपकरण का प्रयोग किया जाता है। लुसाना ने इस विषय पर महत्वपूर्ण प्रयोग किए हैं।
सं.ग्र.-प्रेस्टन : थ्योरी ऑव हीट; साहा : ट्रीटिज़ ऑव हीट। (प्रे.ना.श.)
�