हिंदी विश्वकोश

उष्मागतिकी प्रारंभ में उष्मागतिकी विज्ञान की वह शाखा थी जिसमें केवल उष्मा के कार्य में परिणत होने अथवा कार्य के उष्मा में परिणत होने का विवेचन किया जाता था। परंतु अब इसका क्षेत्र अधिक विस्तृत हो गया है। अब इसमें ताप संबंधी लगभग सभी बातों का अध्ययन किया जाता है। उदाहरणत: यदि हम निकल जैसे किसी चुंबकीय पदार्थ की एक छड़ को एक कुंडली के भीतर रखें और इस कुंडली में बिजली की धारा प्रवाहित कराकर एक चुंबकीय क्षेत्र स्थापित करें तो छड़ की लंबाई में थोड़ा अंतर आ जाएगा, वह थोड़ा गर्म हो जाएगा, और उसकी विशिष्ट उष्मा में भी अंतर हो जाएगा। ऐसे ही यदि नाइट्रोजन तथा हाइड्रोजन का मिश्रण लेकर हम उसमें एक उत्प्रेरक छोड़ दें तो इस मिश्रण में नाइट्रोजन, हाइड्रोजन तथा अमोनिया एक विशेष अनुपात में रहेंगे। ताप में परिवर्तन होने से इस अनुपात में भी परिवर्तन होता है, और यह परिवर्तन उस उष्मा से संबंधित है जो अमोनिया के संश्लेषण की क्रिया में ताप को अपरिवर्तित रखने के लिए उस मिश्रण से निकालनी आवश्यक होती है। ऐसी ही अन्य बातों का अध्ययन भी अब उष्मागतिकी के अंतर्गत होता है जिससे इसका क्षेत्र बहुत विस्तृत हो गया है।

१९वीं शताब्दी के मध्य में उष्मागतिकी के दो सिद्धांतों का प्रतिपादन किया गया था, जिन्हें उष्मागतिकी के प्रथम एवं द्वितीय सिद्धांत कहते हैं। २०वीं शताब्दी के प्रारंभ में दो अन्य सिद्धांतों का प्रतिपादन किया गया है जिन्हें उष्मागतिकी का शून्यवाँ तथा तृतीय सिद्धांत कहते हैं।

उष्मागतिकी का शून्यवाँ सिद्धांत ताप-उष्मागतिकी के अध्ययन में एक नई भावना का समावेश होता है। वह ताप की भावना है। यदि किसी पिंड (बॉडी) के गुणधर्म इस बात पर निर्भर न रहें कि वह कितना गरम अथवा ठंडा है तो उसका पूरा परिचय पाने के लिए उसके आयतन अथवा उसके घनत्व के ज्ञान की ही आवश्यकता होती है। जैसे यदि हम कोई द्रव लें तो यांत्रिकी में यह माना जाता है कि उसके ऊपर दाब बढ़ाने पर उसका आयतन कम होगा। दाब का मान निश्चित करते ही आयतन का मान भी निश्चित हो जाता है। इस तरह इन दो चर राशियों में से एक स्वतंत्र होती है और दूसरी आश्रित अथवा परंतत्र।

परंतु प्रत्यक्ष अनुभव से हम जानते हैं कि आयतन यदि स्थिर हो तो भी गरम या ठंडा करके दाब को बदला जा सकता है। इस प्रकार दाब तथा आयतन दोनों ही स्वतंत्र चर राशियाँ हैं। आगे चलकर आवश्यकतानुसार हम अन्य चर राशियों का भी समावेश करेंगे।

और आगे बढ़ने के पहले हम ऐसी दीवारों की कल्पना करेंगे जो विभिन्न द्रवों को एक दूसरे से अलग करती हैं। ये दीवारें इतनी सूक्ष्म होंगी कि इन द्रवों की पारस्परिक अंतरक्रिया को निश्चित करने के अतिरिक्त उन द्रवों के गुणधर्म के ऊपर उनका अन्य कोई प्रभाव नहीं होगा। द्रव इन दीवारों के एक ओर से दूसरी ओर न जा सकेगा। हम यह भी कल्पना करेंगे कि ये दीवारें दो तरह की हैं। एक ऐसी दीवारें जिनसे आवृत द्रव में बिना उन दीवारों अथवा उनके किसी भाग को हटाए हम कोई परिवर्तन नहीं कर सकते, और उन द्रवों में हम विद्युतीय या चुंबकीय बलों द्वारा परिवर्तन कर सकते हैं क्योंकि ये बल दूर से भी अपना प्रभाव डाल सकते हैं। ऐसी दीवारों को हम 'स्थिरोष्म' दीवारें कहेंगे।

दूसरे प्रकार की दीवारों को हम 'उष्मागम्य' (डायाथर्मानस) दीवारें कहेंगे। ये दीवारें ऐसी होंगी कि साम्यावस्था में इनके द्वारा अलग किए गए द्रवों की दाब तथा आयतन के मान स्वेच्छ नहीं होंगे, अर्थात् यदि एक द्रव की दाब एवं आयतन और दूसरे द्रव की दाब निश्चित कर दी जाए तो दूसरे द्रव का आयतन भी निश्चित हो जाएगा। ऐसी अवस्था में पहले द्रव की दाब एवं आयतन दा_१(P₁) और आ_१(V₁) तथा दूसरे द्रव की दाब एवं आयतन दा_२(P₂) और आ_२(V₂) में एक संबंध होगा जिसे हम निम्नांकित समीकरण द्वारा प्रकट कर सकते हैं :

फ (दा_१, आ_१, दा_२, आ_२) = 0 (१)

�� F (P₁, V₁, P₂, V₂) = 0�� (1)

यह समीकरण उन द्रवों के तापीय संबंध का द्योतक है। दीवार का उपयोग केवल इतना है कि पदार्थ एक ओर से दूसरी ओर नहीं जा सकता। अनुभव द्वारा हम यह भी जानते हैं कि यदि एक द्रव के साथ अन्य द्रवों की तापीय साम्यावस्था हो तो स्वयं इन द्रवों में आपस में तापीय साम्यावस्था होगी। इसी को उष्मागतिकी का शून्यवाँ सिद्धांत कहते हैं।

यदि तापीय साम्यवस्थावाले तीन द्रवों के दबाव तथा आयतन क्रमश:

(दा_१, आ_१), (दा_२, आ_२) तथा (दा_३, आ_३)

(P₁, V₁), (P₂, V2),श् तथा (P₃,V3)

हों तो इनमें समीकरण (१) की भाँति निम्नलिखित समीकरण होंगे :

फ_१ (दा_१, आ_१, दा_२, आ_२) = 0; फ (दा_२, आ_३, दा_३, आ_३) = 0; फ_३(दा_३, आ_३, दा_१, आ_१,) = ०, (२)

f₁ (p₁, V₁, p₂, V₂) = 0;�� f₂(p₂, V₂, p₃, V₃)= 0;� �f₃(p₃, V₃, p₁, V₁,)=0,�� (2)

परंतु उष्मागतिकी के शून्यवें सिद्धांत के अनुसार इन समीकरणों इन समीकरणों में केवल दो ही स्वतंत्र हैं, अर्थात् पहले दोनों समीकरणों की तुष्टि के फलस्वरूप तीसरे की तुष्टि भी अवश्यंभावी है। यह तभी संभव है जब इन समीकरणों का रूप इस प्रकार हो :

फ_१(दा_१, आ_१) = फ_२(दा_२, आ_२) = फ_३(दा_३, आ_३)। (३)

�� f_1�(p₁, V₁) = f₂(p₂, V₂) = f₃(p₃,V₃)�� (3)

इनमें से किसी एक द्रव का उपयोग तापमापी के रूप में किया जा सकता है और उस द्रव के फलन के मान को हम प्रायोगिक ताप की भाँति प्रयुक्त कर सकते हैं। यदि पहले द्रव को तापमापी माना जाए तथा उसके फलन का मान ज (t) हो तो दूसरे द्रव के लिए हमें जो समीकरण मिलेगा अर्थात् फ (दा_२, आ_२)=ज [f₂ (p2 V2)= t] वह दूसरे द्रव का दशासमीकरण (इक्वेशन ऑव स्टेट) कहा जाएगा।

यों तो द्रव के किसी भी गुण का उपयोग तापमापी के लिए किया जा सकता है परंतु दा (p) तथा आ (V) के जिस संबंध का उपयोग किया जाए वह जितना ही सरल होगा उतना ही ताप नापने में सुगमता होगी। हम जानते हैं कि समतापीय अवस्था में अल्प दाबवाली गैस की दाब एवं आयतन का गुणनफल अचर होता है। अतएव दाआ=टमा (pV=R0)श् को ताप नापने के लिए उपयोग में लाया जा सकता है और इस संबंध का उपयोग किया भी जाता है। परंतु यदि (दाब�अयातन) अचर हो तो (दाब�आयतन)^१/२ अथवा (दाब^२�आयतन^२) भी अचर होगा। किंतु इनका उपयोग नहीं किया जाता। दाआ=टमा (p�=R0) का उपयोग करने में क्या लाभ है यह आगे चलकर प्रकट होगा।

२. उष्मागतिकी का प्रथम सिद्धांत, ऊर्जा एवं उष्मा-उष्मागतिकी के शून्यवें सिद्धांत में ताप की भावना का समावेश होता है। यांत्रिकी में, विद्युत् याश् चुंबक विज्ञान में अथवा पारमाण्वीय विज्ञान में, ताप की भावना की कोई आवश्यकता नहीं प्रतीत होती। उष्मागतिकी के प्रथम सिद्धांत द्वारा उष्मा की भावना का समावेश होता है। जूल के प्रयोग द्वारा यह सिद्ध होता है कि किसी भी पिंड को (चाहे वह ठोस हो या द्रव या गैस) यदि स्थिरोष्म दीवारों घेरकर रखें तो उस पिंड को एक निश्चित प्रारंभिक अवस्था से एक निश्चित अंतिम अवस्था तक पहुँचाने के लिए हमें सर्वदा एक निश्चित मात्रा में कार्य करना पड़ता है (ऊर्जा शीर्षक लेख देखें)। कार्य की मात्रा पिंड की प्रारंभिक तथा अंतिम अवस्थाओं पर ही निर्भर रहती है, इस बात पर नहीं कि यह कार्य कैसे किया जाता है। यदि प्रारंभिक अवस्था में दाब तथा आयतन के मान दा₀(p₀) तथा आ₀(V₀) हैं तो कार्य की मात्रा अंतिम अवस्था की दाब तथा आयतन दा (p) तथा आ (V) पर निर्भर रहती है, अर्थात् कार्य की मात्रा दा (P) तथा आ (V)श् का एक फलन है। यदि कार्य की मात्रा का (W) हैं तो हम लिख सकते हैं कि

का=ऊ -ऊ₀(४)

�� W=U-U₀_{��}(४)

यह समीकरण एक राशि ऊ की परिभाषा है जो केवल उस पिंड की अवस्था पर ही निर्भर रहती है न कि इस बात पर कि वह पिंड उस अवस्था में किस प्रकार पहुँचा है। इस राशि को हम पिंड की आंतरिक ऊर्जा कहते हैं। यदि कोई पिंड एक निश्चित अवस्था से प्रारंभ करके विभिन्न अवस्थाओं में होते हुए फिर उसी प्रारंभिक अवस्था में आ जाए तो उसकी आंतारिक ऊर्जा में कोई अंतर नहीं होगा, अर्थात्

f ताऊ =� ० (५)

�� f dU� =� 0� �� (5)

और ताऊ (dU) एक यथार्थ अवकल (परफ़ेक्ट डिफ़रेन्शियल) है।

यदि कोई पिंड एक अवस्था से दूसरी अवस्था में जाए तो ऊ-ऊ₀-का, (U-U₀-W) का मान सर्वदा शून्य के बराबर नहीं होगा। यदि प्रत्येक अवस्था के लिए ऊ (U) का मान ज्ञात कर लिया गया है तो यह अंतर ज्ञात किया जा सकता है। यदि पिंड की दीवारों का कोई भाग उष्मागम्य है तो सर्वदा इस अंतर के बराबर उष्मा उस पिंड को देनी पड़ेगी। यदि उष्मा की मात्रा मा (Q) है तो

मा=ऊ-ऊ₀-का (६)

�� Q=U-U₀-W�� (6)

इस समीकरण में मा (Q)उन्हीं एककों में नापा जाएगा जिसमें क (W), परंतु यदि हमने मा (Q) का एकक पहले ही निश्चित कर लिया है तो हम इस समीकरण द्वारा इन दोनों एककों का अनुपात ज्ञात कर सकते हैं। इस प्रकार जूल के प्रयोग द्वारा हम उष्मा का यांत्रिक तुल्यांक निकाल सकते हैं। इस प्रयोग में मा (Q) शून्य के बराबर होता है और ऊ-ऊ₀(U-U₀) का मान उष्मा के एककों में ज्ञात किया जाता है।

समीकरण (६) उश्मागतिकी के प्रथम सिद्धांत का गणितीय रूप है। इसमें का (Q) वह कार्य है जो बाहर से उस पिंड पर किया जाता है। यदि यह पिंड स्वयं कार्य करे, जिसका परिणाम तोका (dW) हो, और किसी प्रक्रम (प्रोसेस) में निकाय की आंतरिक ऊर्जा जिस परिमाण में बढ़े वह ताऊ (dU)हो तो गिनती उष्मा उस निकाय को दी जाएगी वह तो (dQ) होगी और

तोमा = ताऊ + तोका। (७)

�� dQ = dU + dW�� (7)

इसमें तोमा (dQ) और तोका (dW) में ता (d) को तो (d) इस कारण कर दिया गया है कि ये यथार्थ अवकल नहीं हैं।

और आगे बढ़ने के पहले हम एक ऐसे प्रक्रम का वर्णन करेंगे जिसका उपयोग उषमागतिकी में बहुत किया जाता है। इसे प्राय: स्थैतिक (सिस्टम) के आयतन को एक अत्यणु परिमाण ताआ (dV) से परिवर्तित करें तो इसका ताप भी थोड़ा परिवर्तित हो जाएगा। साम्यावस्था प्राप्त होने पर इसके आयतन में मान ले हम थोड़ा और अत्यणु परिवर्तित करें। इस तरह हम धीरे धीरे अवस्था १ से अवस्था २ में पहुँच जायँगे। यदि हमारे परिवर्तनों का परिमाण धीरे धीरे शून्य की ओर बढ़े तो अंत में १ से २ तक परिवर्तन कहते हैं। ऐसे प्रक्रम का यह भी लक्षण है कि विस्थापनों, किए गए कार्य एवं अवशोषित उष्मा के चिह्नों को उलटकर इस निकाय को अवस्था २ से कारण इन प्रक्रमों को उत्क्रमणीय प्रक्रम कहते हैं। जो प्रक्रम उत्क्रमणीय नहीं होते उन्हें अनुत्क्रमणीय प्रक्रम कहते हैं।

श्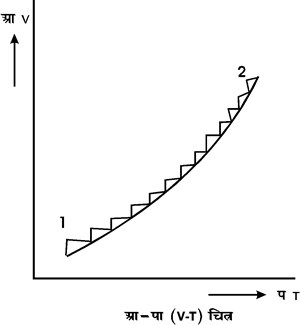

चित्र १. आ-पा (V-T) चित्र

श्

यह सरलता से सिद्ध किया जा सकता है कि यदि किसी निकाय की दाब दा (p) हो तो एक उत्क्रमणीय प्रक्रम में यह जो कार्य करेगा वह दाताआ (pdV) के बराबर होगा। अतएव उष्मागतिकी के प्रथम सिद्धांत को हम इस तरह भी लिख सकते हैं :

तो मा = ता ऊ+ दा ता आ। (८)

�� dQ = dU + pdV �� (8)

३. उष्मागतिकी के प्रथम सिद्धधांत के उपयोग-यदि हम आयतन एवं ताप को स्वतंत्र चर राशियाँ मानें तो :

�� (9)

जहाँ द

अतएव अचर आयतन पर विशिष्ट उष्मा वि_आ(C_V)श् का मान होगा :

�� (10)��

�� (10)

इसी प्रकार अचर दाब पर विशिष्ट उष्मा का मान होगा :

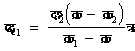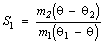�� (11)

अतएव �� (12)

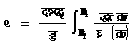�� (12)

जूल-टामसन के प्रयोग में गैस एक पाइप में लगे डाट के एक ओर से दूसरी ओर जाती है। इसमें बाहर से गैस को उष्मा नहीं मिलती। एक ओर से एक पिस्टन दाब दा_१ (p₁) पर गैस को दबाता है। दूसरी ओर गैस दाब दा_२(p₂) वाले एक पिस्टन को पीछे ढकेलती है। यदि गैस का आयतन प्रारंभ में आ_१(V₁) हो तथा अंत में आ_२(V₂)तो पहल पिस्टन द्वारा गैस पर कार्य दा_१ आ_१(P₁V₁) होता है तथा दूसरे पिस्टन को ढकेलने के लिए स्वयं गैस को दा_२ आ_२(p₂V₂) कार्य करना पड़ता है। इस प्रकार गैस को कुल दा_३आ_३-दा_१ आ_१ (p2 V₂- p₁ V₁) का कार्य करना पड़ता है। समीकरण (८) के अनुसार

० = (ऊ_२-ऊ_१)+(दा_२आ_२-दा_१आ_१)

० = (U₂- U₁)+ (P₂V₂- P₁V₁)

अथवा

ऊ_२+ दा_२= आ_२ऊ_१+ दा_१आ_१(13)

�� U₂+ P₂V₂ = U₁+ P₁V_{1��}(13)

यदि हम ऊ+दा आ=पू (U+PV=H) रखें तो राशि पू (H) जूल-टामसन प्रयोग में अचर रहती है। राशि पू (H) को पूर्णोष्मा (टोटल हीट) कहते हैं।

यदि हम किसी निकाय का आयतन न बढ़ने दें तो इसके द्वारा किया गया कार्य शून्य के बराबर होगा। ऐसी अवस्था में जो भी उष्मा उसको मिलेगी उससे उसकी आंतरिक ऊर्जा बढ़ेगी। अर्थात् समीकरण (६) या (८) के अनुसार

तोमा = ऊ₂-उ₁, क्योंकि ताआ = ० (14)

�� dQ = U₂-U₁, क्योंकि dV=0�� (14)

परंतु यदि दाब एक समान रहे और आयतन आ_१(V₁) से बढ़कर आ_२(V₂) हो जाए तो निकाय दा (आ_२-आ_१)[� P(V₂-V₁) ] के बराबर कार्य करेगा और

तोमा = ऊ_२-ऊ_१+दा (आ_२-आ_१) = प_ू२-प_ू१(15)

�� dQ= U₂-U₁+P (V₂-V₁) = H₂-H_{1��}(15)

अर्थात् किसी समदाब प्रक्रम में किसी निकाय को जो उष्मा मिलती है वह उसकी पूर्णोष्मा की वृद्धि के बराबर होती है।

रासायनिक क्रियाओं द्वारा प्राप्त होनेवाली उष्मा के विषय में हेस का नियम भी प्रथम सिद्धांत का ही एक दूसरा रूप है, यद्यपि इसका प्रतिपादन हेस ने उष्मागतिकी के सिद्धांत के पहले ही सन् १८४० में किया था।

४. उष्मागतिकी का द्वितीय सिद्धांत : एंट्रापी-उष्मागतिकी के द्वितीय सिद्धांत द्वारा भी एक नई भावना का समावेश होता है। यह एंट्रापी की भावना है। अन्य भावनाओं की अपेक्षा अधिक अमूर्त होने के कारण इसका बोध भी अधिक कठिन है। उष्मागतिकी के द्वितीय सिद्धांत का वर्णन कई प्रकार से किया जाता है।

क्लाज़िउस तथा लार्ड केलविन के शब्दों में इस सिद्धांत का विवरण उष्मा शीर्षक लेख में दिया जा चुका है।

इस सिद्धांत के अध्ययन में हम अभी सिद्ध करेंगे कि--

''प्रत्येक उष्मागतिकी निकाय की प्रत्येक अवस्था के लिए दो लाक्षणिक गुणधर्म (कैरेक्टेरिस्टिक प्रॉपर्टी) होते हैं, एक परम ताप पा (T) जो केवल प्रायोगिक ताप प (t) पर निर्भर करता है, दूसरा एंट्रापी एं (S) जिसको इस प्रकार में इस निकाय को परिमाण तोमा (dQ) में उसेष्मा मिलें तो

तोमा = पाताएं (dQ= TdS)

होता है। संसार में होनेवाले वास्तविक प्रक्रमों में, जो स्वभावत: अनुत्क्रणीय होते हैं, एंट्रापी की वृद्धि होती है।'' अतएव दूसरे सिद्धांत का वर्णन उपर्युक्त कथन से भी किया जा सकता है।

पहले हम केलविन तथा क्लाज़िउस के कथनों की समतुल्यता सिद्ध करेंगे। इसके लिए हम यह सिद्ध करेंगे कि यदि केलविन का कथन असत्य हो तो क्लाज़िउस का कथन भी असत्य होगा। इसी तरह यदि क्लाज़िउस का कथन असत्य हो तो केलविन का कथन भी असत्य होगा।

यदि केलविन का कथन असत्य हो अर्थात् यदि उष्मा को किसी चक्रीय प्रक्रम में संपूर्णत: कार्य में परिवर्तित करना संभव हो तो घर्षण द्वारा इस कार्य को पुन: उष्मा में परिवर्तित करके किसी अन्य निकाय में पहुँचाया जा सकता है, चाहे यह दूसरा निकाय किसी भी ताप पर हो। इस प्रकार उष्मा को निम्न तापवाले निकाय से उच्च तापवाले निकाय में ले जाना संभव होगा। इस तरह क्लाज़िउस का कथन भी असत्य सिद्ध हो जाएगा।

यदि सिद्ध करने के पहले कि यदि क्लाज़िउस का कथन असत्य हो तोश् केलविन का कथन भी असत्य होगा, हम इस बात का अध्ययन करेंगे कि उष्मा को कार्य में कैसे परिवर्तित करते हैं। इसके लिए हम उस चक्रीय परिवर्तन का अध्ययन करेंगे जिसे कार्नो चक्र (कार्नो साइकिल) कहते हैं।

कार्नो चक्र-कार्नो चक्र का वर्णन उष्मा शीर्षक लेख में संक्षेप में किया गया है। कल्पना करें कि एक निकाय है जिसकी अवस्था दो चर राशियों दा (p) तथा आ(V)द्वारा निश्चित की जा सकती है। यह भी मान लें कि तापों प_१(t₁) प_२(t₂)पर उष्मा के दो बहुत बड़े स्रोत अथवा कुंड हैं जिनकी उष्माधारिता अनंत है प_१(t₁) तथा प_२(t₂) किसी भी प्रायोगिक तापक्रम पर नापे गए हैं और हम मान लेंगे कि प_२(t₂) से प_१(t₁) अधिक है। हम यह भी कल्पना करेंगे कि निकाय, जो तरल है, एक बेलनाकार पात्र के भीतर है और उसपर किसी पिस्टन द्वारा दबाव पड़ रहा है। पिस्टन तथा बेलन के पार्श्व उष्मा के चालक नहीं हैं, किंतु बेलन की पेंदी उष्मा की चालक है। एक ऐसी टोपी भी है जो बेलन की पेंदी में लगाई जा सकती है और जो उष्मा की चालक नहीं है। पहले हम बेलन को ताप प_१ (t₁) वाले स्रोत पर रखते हैं। इस तरह तरल निकाय का ताप भी प_१ (t₁) हो जाएगा। मान लीजिए इसकी अवस्था दा-आ (P-V) रेखाचित्र में बिंदु क द्वारा निश्चित हो रही है। अब मान लीजिए कि तरल निकाय प्राय:-स्थैतिक प्रक्रम से फैल रहा है। ऐसी दशा में पिस्टन की दाब के विरुद्ध तरल निकाय कुछ कार्य करेगा और स्रोत से कुछ उष्मा ग्रहण करेगा जिसका परिमाण मान लेते है कि मा_१ (Q₁) है। इस प्रक्रम में तरल निकाय का ताप एक समान रहेगा और इस परिवर्तन को दा-आ (P-V) रेखाचित्र में समतीय वक्र क ख श्द्वारा दिखलाया जा सकता है। अब बेलन की पेंदी पर हम टोपी लगा देते हैं जिससे तरल निकाय में उष्मा का प्रवेश न हो सके। तब हम तरल निकाय को प्राय:स्थैतिक प्रक्रम से और फैलने देते हैं जिससे इसका ताप प_२(t₂)श् हो जाता है। दा-आ (P-V) रेखाचित्र में इस परिवर्तन को स्थिरोष्म वक्र ख ग द्वारा दिखलाया जा सकता है। अब कुचालक टोपी उतारकर हम बेलन को तापश् प_२(t₂) वाले स्रोत पर रखते हैं और प्राय:स्थैतिक प्रक्रम से इसका संपीडन करते हैं। इससे तरल निकाय पर पिस्टन द्वारा कुछ कार्य होगा और कुछ उष्मा तरल निकाय से स्रोत में जाएगी जिसका परिमाण, मान लेते हैं, मा_२(Q₂) है। दा-आ (P-V) रेखाचित्र में यह परिवर्तन समतापीय वक्र ग घ द्वारा दिखलाया जा सकता है। बिंदु घ इस तरह चुना जाता है कि वह उसी स्थिरोष्म वक्र पर हो जिस पर क श्है। अब टोपी लगाकर फिर प्राय:स्थैतिक प्रक्रम से तरह निकाय का संपीडन किया जाता है जिससे इसका ताप फिर प_१(t₁) हो जाए और तरल निकाय अपनी प्रारंभिक अवस्थ में जा जाए।

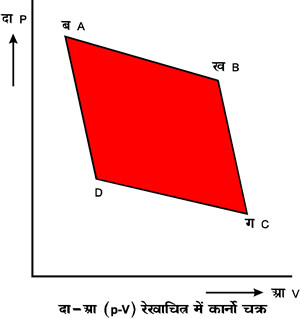
इस चक्रीय परिवर्तन का फल केवल यह हुआ कि प_१(t₁) तापवाले स्रोत में से परिमाण मा_१(Q₁) में उष्मा ली गई है। इसमें कुछ भाग कार्य में परिणत हुआ है और परिमाण मा_२(Q₂) में उष्मा ताप प_२(t₂) वाले स्रोत में चली गई है। क्योंकि इस चक्र में सभी परिवर्तन प्राय:स्थैतिक हैं, अतएव इस चक्रीय परिवर्तन में जो कार्य होता है वह �दाताआ [�pdv] के बराबर होता है। जो क्षेत्र कखगघ के क्षेत्रफल के बराबर होता है। यदि यह कार्य का (W) के बराबर है तो प्रथम सिद्धांत के अनुसार

का=मा_१-मा_२ (१६)

(W=Q1-Q₂) (१६)

कानों चक्रा की बड़ी विशेषता यह है कि इसके सारे परिवर्तन प्राय:स्थैतिक हैं। अतएव इसे उलटी दिशा, अर्थात, क घ ग ख श्दिशा में भी पूरा किया जा सकता है। इस प्रक्रम में तरल निकाय के ऊपर परिमाण में कार्य किया जाएगा, ताप प_२(t₂) वाले स्रोत से तरल निकाय परिमाण मा_२(Q₂) में उष्मा लेगा और ताप प_१(t₁) वाले स्रोत में परिमाण मा_१(Q₁) में उष्मा देगा।

पहले हम यह सिद्ध करेंगे यदि का (W) धन राशि हो तो मा_१(Q₁) तथा का_२(Q₂) भी धन राशियाँ होंगी। पहले मान लेते हैं कि का_२(Q₂) धन राशि नहीं है। अर्थात् ताप प_२(t₂) वाले स्रोत से परिमाणश् मा_२(Q₂) में उष्मा ली गई है, उसमें उष्मा पहुँचाई नहीं गई है। अब दोनों स्रोतों को उस समय तक एक दूसरे को स्पर्श करने दिया जा सकता है जब तक परिमाणश् मा_२(Q₂) में में उष्मा स्रोत प_१(t₁) से स्रोत प_२(t₂) में पहुँच जाए। इन सब परिवर्तनों का फल यह होगा कि स्रोत प_१(t₁) से कुछ उष्मा लेकर उसे संपूर्णतया कार्य में परिणत कर दिया गया है। परंतु वह केलविन के कथन के विरुद्ध है। अतएव मा_२(Q₂) धनराशि है। क्योंकि मा_१=मा_२+का (Q₁=Q₂+W) अत: मा_१(Q₁) भी धन राशि है।

अब बड़ी सुगमता से यह सिद्ध किया जा सकता है कि यदि क्लाज़िउस का कथन असत्य हो तो केलविन का कथन भी असत्य होगा। क्योंकि यदि किसी चक्रीय परिवर्तन से ताप प_२(t₂) वाले स्रोत से ताप प_१(t₁) वाले स्रोत में परिमाण मा_१(Q₁) में उष्मा पहुँचना संभव हो तो कार्नो चक्र की सहायता से ताप प_१(t₁) वाले स्रोत से उष्मा मा_१(Q₁) लेकर इसमें से कार्य का (W) किया जा सकता है तथा शेष मा_२=मा_१-का (Q₁=Q₂-W) ताप प_२(t₂) वाले स्रोत में पहुँचाई जा सकती है। इस पूरे परिवर्तन का यह फल होगा कि किस अन्य परिवर्तन के बिना ही परिमाण मा_१-मा_२-का (Q₁-Q₂=W) में ताप प_२(t₂) वाले स्रोत की उष्मा को कार्य में परिणत कर दिया गया है। यह केलविन के कथन के विरुद्ध है, अर्थात् यदि क्लाज़िउस का कथन असत्य हो तो केलविन का कथन भी असत्य होगा।

किसी चक्रीय परिवर्तन में जितना कार्य किया जाए उसका ऊँचे तापवाले स्रोत से ली गई उष्मा के साथ जो अनुपात है उसे उस चक्र की कार्यक्षमता (सफ़िशेंसी) कहते हैं। अर्थात कार्यक्षमता=का/मा (W/Q)।

अब हम सिद्ध करेंगे कि कार्नो चक्र की कार्यक्षमता सबसे अधिक होती है और केवल प_१ तथा प_२ (t तथा t_२) पर ही निर्भर रहती है। मान लेते हैं कि कोई अनुत्क्रमणीय चक्र ऐसा है जिसकी कार्यक्षमता कार्नो चक्र से अधिक है। हम दो तरल निकाय लेते हैं जिनमें एक तापों प_१(t ) तथा प_२ (t₂) के बीच कार्नों चक्र पूरा करता है तथा दूसरा अनुत्क्रमणीय चक्र कार्नो चक्र में तरल निकाय ताप प_१(t ) तथाश् प_२ (t₂) के बीच कार्नो चक्र पूरा करता है तथा दूसरा अनुत्क्रमणीय चक्र कार्नो चक्र में तरल निकाय ताप प_१(t ) वाले स्रोत से उष्मा मा_१ (Q₁) लेकर कार्य का (W) करता है और शेष मा_२=मा_१-का� (Q₂=Q₁-W�) को ताप प_२ (t₂) वाले स्रोत को दे देता है। अनुत्क्रमणीय चक्र ताप प_१(t₁ ) वाले स्रोत से उष्मा मा_१� (Q₁�) लेकर कार्य का� (W�) करता है और शेष मा�_२=मा�_१-का� (Q₂�=Q₁�-W�) को तापश् प_२ (t₂) वाले स्रोत को दे देता है। हम इन चक्रों का ऐसा नियंत्रण करेंगे कि मा_१=मा_१� (Q₁=Q₁�); अतएव का�>का (W�>W) क्योंकि हमने मान लिया है कि अनुत्क्रमणीय चक्र अधिक कार्यक्षम है। अब हम इन दोनों को एक साथ चलाते हैं और अनुत्क्रमणीय चक्र का उपयोग उत्क्रमणीय चक्र को विपरीत दिशा में चलाने में करते हैं। इस प्रकार तापश् प_२ (t₂) वाले स्रोत से मा_२=मा_२� (Q₂=Q₂�) परिमाण में उष्मा कार्य का�>का (W�>W) में परिणत हो जाएगी और यह केलविन के नियम के विरुद्ध है। अतएव कोई अनुत्क्रमणीय चक्र कार्नो की अपेक्षा अधिक कार्यक्षम नहीं हो सकता।

यदि दोनों ही चक्र उत्क्रमणीय हों तो इसी प्रकार हम सिद्ध कर सकते हैं कि न तो पहला दूसरे से अधिक कार्यक्षम है, न दूसरा पहले से। अर्थात् दोनों की कार्यक्षमता बराबर है और यह कार्यक्षमता किसी तरह निकाय पर निर्भर नहीं रहती, केवल स्रोतों के तापों पर निर्भर रहती है अतएव

मा_१/मा_१=फ (प_१,प_२)। (१७)

Q/Q₂= f (t₁,t₂)�� (१७)

अब हम तापों प_१,प_२(t₁,t₂) तथा प_३(t₃) पर तीन स्रोत लेते हैं। एक कार्नो चक्र स्रोत प_१श्(t₁) से उष्मा मा_१(Q₁) लेता है और स्रोतश् प_२(t₂) को उष्मा मा_२(Q₂) देता है। दूसरा कार्नो चक्र स्रोत प_२(t₂) से उष्मा मा_२(Q₂) लेता है और उष्मा मा_३(Q₃) स्रोत प_३(t₃) को देता है अतएव

मा_१/मा_२=फ (प_१,प_२) ; मा_२/मा_३=फ (प_२,प_३)। (१८)

Q_१/Q₂= f (t₁,t₂) ; Q_२/Q₃= f (t₂,t₃)� (१८)

एक तीसरा कार्नो चक्र ऐसा है जो स्रोत प_१श्(t₁) से उष्मा मा_१(Q_१) लेता है और स्रोत प_३(t₃) को उष्मा मा_३(Q₃) देता है; अतएव

मा_१मा_३= फ (प_१,प_२)। (१९)

Q/Q₃= f (t₁,t₃)�� (१९)

समीकरणों (१८) तथा (१९) के कारण

फ (प_१,प_२) = फ (प_१,प_३)/फ (प_२,प_३)। (२०)

�f (t₁,t₂) = f (t₁,t₃) / f (t₂,t₃)�� (२०)

जो प_१,प_२,प_३(t₁,t₂,t₃) के सभी मानों के लए ठीक है। इस समीकरण के बाईं ओर प_३(t₃) नहीं है। अतएव दाहिनी ओर भी प_३(t₃) को नहीं होना चाहिए। यह तभी होगा जब फ (प_१,प_२) [ f (t₁,t₂)] फलन का स्वरूप निम्नलिखित हो :

फ (प_१,प_२) = फी (प_१)/फी (प_२)। (२१)

�f (t₁,t₂) = g (t₁) / g (t₂)�� (२१)

इसमें फी (प) [ g (t)] प्रायोगिक ताप का फलन है, जिसका मान हम धनात्मक ले सकते हैं, क्योंकि म_१ (Q₁) तथा म_२ (Q₂) धन राशियाँ हैं। ताप के इस फलन को अथवा इसके गुणज (मल्टिपुल) को हम परम ताप के बराबर मान सकते हैं। अथार्त् पा=अ फी (प), [ T=a g (t)] जिसमें पा �(T) परम ताप है। इस प्रकार

मा/मा_२= फ (पा_१/पा_२)। (२२)

Q/Q₂= (T₁/T₂)�� (२२)

इस परम ताप की विशेषता यह है कि इसका मान किसी पदार्थ के गुणों पर निर्भर नहीं रहता। इसी कारण उष्मागतिकी में इसी पैमाने का उपयोग किया जाता है। इसका आकार निश्चित करने के लिए इस तापक्रम में भी हम पानी के हिमांक तथा क्वथनांक के बीच का अंतर १०० के बराबर मानेंगे। यदि इन बिंदुओं का मान पा_० (T_०) तथा तथा पा_१०० (T₁₀₀) है तो

�� (२३)

यदि प्रत्यक्ष या अप्रत्यक्ष रूप से मा_१०० (Q₁₀₀) तथा मा_० (Q_०) का मान ज्ञात कर लिया जाए तो पा_० (T_०) का मान निकाला जा सकता है। इस तरह यह ज्ञात किया गया है कि पा_० (T_०)= २७३.१६.

कार्नो चक्र में मा_१ (Q) तथा मा_२(Q₂) का अनुपात पा_१ (T₁) तथा पा_२(T₂) के अनुपात के बराबर है,

अर्थात्श्श् मा_१/मा_२=पा_१/पा_२। �� (Q₁/Q₂= T₁/T₂)

�� मा/मा_१-मा_१/पा_२=०श्श् श् श्(Q₁/T₂- T₁/T₂=0)

�� (मा/पा)=०, श्श् [�(Q/T)=0],�� (24)

जिसमें मा (Q) निकाय द्वारा ली गई उष्मा का परिमाण है अैर यदि निकाय उष्मा लेता है तो यह धन होगा; यदि निकाय उष्मा देता है तो यह ऋण होगा।

अब यह दिखलाना सरल है कि आदर्श गैस-तापमापी पर नापा ताप वही है जो परम-ताप-क्रम का ताप (आदर्शगैस्-तापमापी के लिए तापमान शीर्षक लेख देखें)। आदर्श गैस का समीकरण है

दा आ = झ थ, (२५)

PV=Rq, (२५)

जिसमें थ (q) आदर्श गैस तापक्रम पर ताप है और झ (R) एक अचर है। यदि कार्नो चक्र में जो तरल प्रयुक्त हो रहा है वह एक आदर्श गैस है तो मा_१ (Q₁) उस कार्य के बराबर होगा जो आदर्श गैस बिंदु क से ख तक फैलने में करती है। यदि गैस का आयतन बिंदुओं क, ख, ग तथा घ पर क्रमानुसार आ_१, आ_२, आ_३ (V₁, V₂, V₃) तथा आ_४ (V₄) है तोश्

�� (२६)

इसी प्रकार

मा झ थ_२ लघु {आ_३/आ_४}। (२७)

Qq₂=R₂ log_e {V₃/V₄}�� (२७)

क्योंकि बिंदु ख तथा ग एक ही स्थिरोष्म पर हैं, अतएव

थ_१ आ_२^गा^-१=थ_२ आ_३^गा^-१; (q₁ V₂y^-1=q₂ V₃y^-1;)

अर्थात्

थ_१/थ_२=(आ_३/आ_२)^गा^-१। �(q₁ /q₂=(V₃/V₂)y^-1;)�� (२८)

इसी प्रकार क तथा घ भी एक ही स्थिरोष्म पर हैं, अतएव

थ_१ आ_२^गा^-१=थ_२ आ_४^गा^-१ (q₁ V₂y^-1=q₂ V₄y^-1)

अर्थात् थ_१/थ_२=(आ_४/आ_१)^गा^-१=(आ_३/आ_२)^गा^-१

�(q₁ /q₂=(V₄/V₁)y^-1=V₃/V₂)y^{-1��}

अर्थात् आ/आ_२=(आ_३/आ_२)। (V₄/V₁)=V₃/V₂)

अतएव आ_३/आ_४=(आ_२/आ_१)। (V₃/V₄)=V₂/V₁)�� (२९)

समीकरणों (२६), (२७) एवं (२९) की सहायता से

मा_१/मा_२=(थ_३/थ_२)। �(Q₁ /Q₂=q₁ /q₂ )�� (३०)

अब समीकरणों (२२) तथा (३०) की सहायता से

थ_१/थ_२=पा_१/पा_२)। (q₁ /q₂=T₁ /T₂ ) (३१)

आदर्श गैस-तापमापी में भी पानी के हिमांग तथा क्वथनांक में १००� का अंतर है। अतएव आदर्श गैसतापमापी के ताप एवं परम तापक्रम के ताप एक ही हैं। दाआ= झथ �(PV=Rq ) का उपयोग करने का यही लाभ है।

अब हम कल्पना करेंगे कि कोई निकाय एक चक्रीय परिवर्तन पूरा करता है। इस परिवर्तन में यह निकाय कई स्रोतों से उष्मा ग्रहण करता है या उनको ऊष्मा देता है। इन स्रोतों के ताप पा_१, पा_२,..., पा_म(T₁ T₂... T_m) हैं। विनिमय की गई उष्मा का परिमाण क्रमश: मा_१, मा_२,..., मा_म(Q₁ Q₂... Q_m) है। जो निकाय उष्मा लेता है उसे हम धन मानेंगे तथा जो देता है उसे ऋण। अब हम सिद्ध करेंगे कि

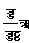
�� o।�� 0.�� (३२)

बराबरी का चिह्न उस दशा में लागू हाता है जब निकाय द्वारा पूरा किया गया चक्रीय परिवर्तन उत्क्रणीय हो।

इसको सिद्ध करने के लिए हम यह कल्पना करेंगे कि इस म (m) स्रोतों के अतिरिक्त एक और स्रोत है जिसका ताप पा_०(T_० ) है और इस स्रोत और उपर्युक्त स्रोतों के बीच कार्नो चक्र का_१, का_२,..., का_म(W₁ W₂... W_m) क्रमानुसार कार्य करते हैं जिनके फलस्वरूप उपर्युक्त स्रोतों में उष्मा क्रमानुसार परिमाण मा_१, मा_२,..., मा_म(Q₁ Q₂... Q_m) में पहुँच जाती है। समीकरण (२२) के अनुसार य वें (xth) कार्नो चक्र द्वादा य वें (xth) स्रोत में मा_१ (Cx) परिमाण में उष्मा पहुँचाने के लिए ताप पा_०(T_० ) वाले स्रोत में से य वाँ चक्र जितनी उष्मा लेगा उसका परिमाण होगा

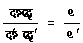
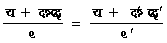�� (३३)

इस प्रकार ताप वाले स्रोत से जो कुल उष्मा ली जाएगी उसका परिमाण

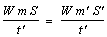
�� (३४)

होगा। निकाय न (n) तथा म (m) कार्नो चक्रों के चक्रीय परिवर्तन पूरा

करने के फलस्वरूप म (m) स्रोतों में उतनी उष्मा पहुँच जाएगी जितनी प्रत्येक में से निकाय न (n) ने ग्रहण की थी। क्योंकि न (n) तथा क_१, क_२,... (W₁, W₂...) आदि इन चक्रीय परिवर्तनों को पूरा करके अपनी प्रारंभिक अवस्था में पहुँच जाएँगे, इसलिए इन चक्रीय परिवर्तनों का फल केवल यह होगा कि ताप पा_० (T_०) वाले स्रोत का परिमाण भा की उषमा कार्य में परिवर्तित हो गई। यदि मा_० (Q_०) धन राशि हो तो यह फल केलविन के नियम के विरुद्ध होगा। अतएव मा_०�० (Q_०�0) अर्थात्

०। 0�� (३५)

यदि निकाय न (n) श्द्वारा पूरा किया चक्र उत्क्रमणीय हो तो यह उस चक्रीय परिवर्तन को उलटी दिशा में पूरा कर सकता है। ऐसी दशा में प्रत्येक मा_अ(Q_x) को चिह्न बदल जाएगा। अर्थात् जब हम इस परिणाम पर पहुँचेंगे कि

०।0.

अर्थात् ०।श् �� (३६)

श्

(३५) तथा (३६) की असमताएँ एक साथ तभी ठीक हो सकती हैं जब

०।श् 0�� (३७)

अतएव चक्र यदि उत्क्रमणीय हो तो समीकरण (३७) ठीक होगा और यदि अनुत्क्रमणीय हो तो असमता (३२) लागू होंगी।

यदि स्रोतों की संख्या परिमित होने के स्थान पर अपरिमित हो तथा इनमें प्रत्येक निकाय अत्यणु परिमाण में उष्मा ग्रहण करे तो हमें संकलन के स्थान पर समाकलन का प्रयोग करना पड़ेगा और हमें यह फल मिलेगा कि

०, �� 0,�� (३८)

जिसमें समानता का चिह्न उत्क्रमणीय चक्र के लिए है और असमानता का चिह्न अनुत्क्रमणीय चक्र के लिए है।

यदि दा आ (P-V) रेखाचित्र ३ में क एवं ख दो बिंदु निकाय की साम्यावस्थाओं के सूचक हैं तो निकाय क से ख बिंदु तक साधारणतया कई उत्क्रमणीय पथों द्वारा ले जाया जा सकता है। मान लेते हैं कि क_१ख एवं क_२ख ऐसे दो पथ हैं। अतएव क_१ख_२क एक उत्क्रमणीय चक्र है और इस चक्र के लिए समीकरण (३८) के कारण

०। 0

इस समाकलन को दो खंडों में विभाजित किया जा सकता है। एक क_१ख पथा से दूसरा ख_२क पथ से। अर्थात्

०

श्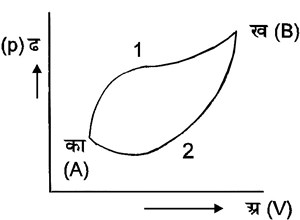

चित्र : ३

अतएव ।

�� (३९)

श्

अर्थात् समाकलन �तोमा/पा (�dQ/T) श्का मान पथ पर नहीं निर्भर रहता, केवल क एवं ख दोनों अवस्थाओं पर ही निर्भर रहता है। अतएव इस समीकरण की सहायता से हम निकाय के नए लाक्षणिक गुणधर्म को निश्चित कर रहे हैं जिसे एंट्रापी कहते हैं।

अतएव

एं_ख-एं_क=।�� (४२)

एक अत्यण उत्क्रमणीय परिवर्तन के लिए, जिसमें निकाय उष्मा तोमाश् (dQ) ताप पाश् (T) पर ग्रहण करता है, इस एंट्रापी की वृद्धि ताएंश् (dS) होगी जहाँ

पा ताएं=तोमा

TdS=dQ �� }�� (४१)

उष्मागतिकी के पहले सिद्धांत के कारण

पा ताएं=ताऊ+दा ताआ (TdS=dU+PdV);

अतएव तोमा=ताऊ+दा ताआ

TdS=dU+PdV�� }�� (४२)

श्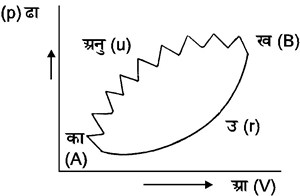

चित्र : ४

यदि कोई चक्र अंशत: अत्क्रमणीय एवं अनुत्क्रमणीय हो तो असमता (३८) लागू होगी और

< ० (४३)

<�� (४३)

जिनमें क उ ख (ArB) उत्क्रमणीय पथ है तथा ख अनु क (BuA) अनुत्क्रमणीय पथ है। असमता (४३) की सहायता से

०>

�� >

अर्थात् ०> -[ एं_ख-एं_क]�� (४४)

> �� (४४)

श्

(४०) तथा (४४) की सहायता से हम देखते हैं कि

एं_ख-एं_क �� (४५)

तथा पा ताएं � (ताऊ+दा ताआ) � (ताऊ दा ताआ)

TdS�dU+PdV� dH-VdP�� }�� (४६)

जिसमें समता का चिह्न उत्क्रमणीय परिवर्तन के लिए लागू है एवं असमता का चिह्न अनुत्क्रमणीय परिवर्तन के लिए।

५. उष्मागतिकीय विभव तथा मैक्सवेल के संबंध-यदि निकाय पूर्णत: पृथक हो तो उसके लिए तोमा=० (d Q=०)। अतएव ऐसे निकाय के लिए

श्श् ताएं�०

dS�० } (४७)

अर्थात् किसी भी पृथक निकाय में स्वभावत: जो भी परिवर्तन होते हैं उनके फलस्वरूप एंट्रापी बढ़ी ही है, घटती नहीं, और इस निकाय की यह अवस्था सबसे अधिक स्थायी होती है जसमें एंट्रापी का मन सबसे अधिक रहता है।

परंतु सभी निकाय ऐसे नहीं होते जिनका बाह्य संपर्क कुछ भी न हो। अतएव हम ऐसे निकायों का भी विवेचन करेंगे जो पूर्णतया पृथक भी न हो। अतएव हम ऐसे निकायों का भी विवेचन करेंगे जो पूर्णतया पृथक न हों। असमता (४६) को हम एक और प्रकार से लिख सकते हैं। वह है

दा ताआ�पा ताएं-ताऊ,

�� p dV�TdS-dU�� }�� (४८)

समतापीय प्रक्रमों के लिए (४८) इस प्रकार भी लिखा ला सकता है।

दा ताआ�-(ताऊ-पा एं)=-ताफा

�� p dV�-d(U-TS)=-dF�� }�� (४९)

जिसमें फा=ऊ-पाएं (F=U-TS)। फा (F) को स्वतंत्र ऊर्जा कहते हैं। असमता (४९) का यह अर्थ है कि कोई निकाय नियत ताप पर उत्क्रमणीय परिवर्तनों में उतना ही कार्य कर सकता है जितनी कमी उसकी स्वतंत्र ऊर्जा में होती है। अनुत्क्रमणीय परिवर्तनों में कार्य की मात्रा स्वतंत्र ऊर्जा में कमी की मात्रा से कम होती है। असमता (४९) को यों भी लिखा जा सकता है :

ताफा�-(दा ताआ)। dF�-(PdV)�� (५०)

अर्थात् नियत ताप तथा निकयत आयतन पर वास्तविक (अतएव अनुत्क्रमणीय परिवर्तनों में स्वतंत्र ऊर्जा कम होती है तथा निकाय की वह अवस्था सबसे अधिक स्थायी होती है जिसमें स्वतंत्र ऊर्जा सबसे कम हाती है।

यदि किसी निकाय का केवल ताप ही नियत रहे अपितु इसका दबाव भी नियत रहे, तो असमता (४९) से हम एक अन्य असमता प्राप्त कर सकते हैं। वह है

०�-ता (ऊ-पा एं+दा आ)=-ताफू

०�-d (U-TS+PV)=-dG�� }�� (५१)

जिसमें फू=ऊ-पाएं+दाआ) (G=U-TS+PV)। फू (G) को स्वतंत्र पूर्णोष्मा अथवा गिब्ज़ की स्वतंत्र ऊर्जा कहते हैं; फा को हेल्महोल्ट्स की स्वतंत्र ऊर्जा कहते हैं। असमता (५१) का अर्थ यह है कि समतापीय एवं समदाबीय वास्तविक परिवर्तनों में गिब्ज़ की स्वतंत्र ऊर्जा कम होती है और वह अवस्था सबसे अधिक स्थायी होती है जिसमें गिब्ज़ की स्वतंत्र ऊर्जा सबसे कम रहती है।

अब तक हम उष्मागतिकीय निकायों से संबंधित आठ राशियों की चर्चा कर चुके हैं। ये हैं दा, आ, पा, एं �(P, V, T, S) एवं श्ऊ, पू, फा (U, H, F,) औरश् फू (G)। इनमें पिछली चार राशियों की विमितियाँ (डाइन्मेन्शन्स) वे ही हैं जो ऊर्जा की। इन चारों राशियों को उष्मागतिकीय विभव कहते हैं। किसी भी उष्मागतिकीय निकाय की प्रत्येक अवस्था के लिए प्रथम चार राशियों का एक निश्चित मान होता है जो उस पथ पर निर्भर नहीं करता जिससे निकाय उस अवस्था को प्राप्त हुआ है। इसी तरह पिछली चार राशियों के भी निकाय की प्रत्येक अवस्था के लिए निश्चित मान होते हैं। अर्थात् ताऊ, (dU) तापू, (dH) ताफा (dF) तथा ताफू (dG) चारों यथार्थ अवकल हैं तथा उत्क्रमणीय परिवर्तनों के लिए इनका मान निम्नांकित समीकरणों द्वारा प्रकट होता है :

ताऊ=पा ताएं-दा ताआ। dU =T dS-p dV,�� (५२)

तापू=ताऊ+दा ताआ+आ तादा=पा ताएं+आ तादा, (५३)

dH =dU+p dV+VdP=T dS+SdT�� (५३)

ताफा=ताऊ-पा ताएं-एं तापा=-दा ताआ-एं तापा, (५४)

dF =dU-T dS-S dT=-PdV-S dT�� (५४)

ताफू=ताऊ-पा ताएं-एं तापा+दा ताआ+आ तादा (५५)

dG =dU-T dS-S dT+pdV+VdP=Vdp-S dT (५५)

समीकरण (५२) में एंट्रापी एं (S) तथा आयतन आ (V) स्वतंत्र चर राशियाँ हैं तथा इनमें हमें निम्नलिखित फल मिलते हैं :

��

परंतु ,

अतएव ।

�� (५६)

इसी प्रकार समीकरणों (५३), तथा (५५) से हमें तीन अन्य फल मिलते हैं :

�� (५७)

�� ,�� (५७)

�� ,�� (५८)

,�� (५८)

�� । (५९)

�� (५९)

समीकरणों (५६), (५७), (५८) तथा (५९) में जो संबंध दिखाए गए हैं उन्हें मैक्सवेल के संबंध कहते हैं।

समीकरण (५४) से

एं।

�� (६०)

अतएव फा=ऊ-पाएं=ऊ+पा ,

�� (६०)

अर्थात् 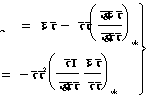�� (६१)

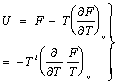�� (६१)

श्

समीकरण (६१) को गिब्ज़-हेल्महोल्ट्स-संबंध कहते हैं।

इसी प्रकार पू तथा फू के बीच भी गिब्ज़-हेल्महोल्ट्स-संबंध प्राप्त किया जा सकता है। समीकरण (५५) से

एं। �� (६२)

अतएव फू=ऊ+दाआ-पाएं=पू-पाएं

�� (६२)

अथवा 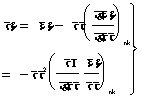�� (६३)

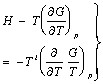�� (६३)

श्

समीकरणों (६१) एवं (६३) की सहायता से समीकरणों (५४) तथा (५५) को निम्नलिखित प्रकार से लिखा जा सकता है :

�� (६४)

तथा �� (६५)

�� (६५)

अतएव

तथा (६६)

तथा �� (६६)��

६. जूल-टामसन-प्रभाव-हम पहले देख चुके हैं कि जूल-टामसन-प्रयोग में पूर्णोष्मा पू का मान नियत रहता है। यदि हम ताप तथा दाब को स्वतंत्र चर राशियाँ मानें तो

��

अतएव जूल-टामसन-प्रयोग के लिए

��

अतएव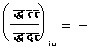

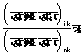
समीकरण (५३) के अनुसार

�� (६७)

तथा समीकरण (६६) के अनुसार

�� (६८)

��

अतएव 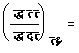। (६९)

�� (६९)

आदर्श गैस के लिए पा (तआ/तपा) _दा-आ=०;[T(dV/dT)_p–v=o] श्अतएव आदर्श गैस पर जूल-टामसन-प्रयोग का कोई असर नहीं पड़ेगा। जिस गैस के लिए समीरण (६९) की दाईं ओर की राशि धन होगी वह इस प्रयोग में ऊँची दाब से नीची दाब की ओर जाने पर ठंडी हो जाएगी। जिस गैस के लिए दाईं ओर की राशि ऋण होगी वह ऊँची दाब से नीची दाब की ओर जाने पर गरम हो जाएगी। हाइड्रोजन तथा हीलियम साधारण ताप पर इस प्रयोग में गरम हो जाती है, परंतु ताप पर्याप्त कम कर देने से ये भी ठंडी होती हैं।

७. दोनों विशिष्ट उष्माओं का अंतर-समीकरण (१२) में हमने दोनों विशिष्ट उष्माओं का अंतर निकाला है। परंतु इस अंतर के व्यंजक में (तऊ/तआ)_पा (U/V)_T एक ऐसी राशि है जिसका मान साधारणतया प्रयोग द्वारा ज्ञात नहीं किया जा सकता है। अब हम इस अंतर को ऐसी राशियों के रूप में रखेंगे जिनका मान प्रयोग द्वारा ज्ञात किया जा सकता है। समीकरण (६६) के अनुसार

��

अतएव �� (७०)

=डढआदापा,

�� (७०)

जिसमें ड (�) प्रसार गुणांक है तथा ढ (B) दवाब बढ़ने का गुणांक है। गैसों के लिए सूत्र (७०) इस रूप में है कि वि_दा (Cp) एवं वि_आ (Cv)� का अंतर ज्ञात किया जा सके। परंतु द्रवों के लिए अथवा ठोस पदार्थों के लिए यह उपयुक्त रूप में नहीं है। इनके लिए हम इसको निम्नलिखित रूप में रखते हैं :

ड/ण (७१)

�� (७१)

जिसमें ण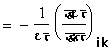 संपीड्यता।

(संपीड्यता)

अतएव वि_दा- वि_आ पा आ ड^२/ण। (७२)

�� (७२)

८. आदर्श गैस की एंट्रापी-समीरकरण (४०) एवं (४२) की सहायता से किसी अवस्था में आदर्श गैस की एंट्रापी का क्या मान होगा, यह निकाला जा सकता है। समीकरण (४२) में

��

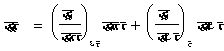
समीकरण (६६) की सहायता से यह सिद्ध किया जा सकता है कि आदर्श गैस के लिए उपर्युक्त व्यंजक में दाईं ओर का दूसरा पद शून्य के बराबर है।

अतएव ताएं

��

अत: एं = वि_दाश्लघु पा - झ लघु दा + एं_० , (७३)

�� (७३)

जिसमें एं (S) श्परमशून्य ताप पर एंट्रापी का मान है।

९. रासायनिक विभव-अभी तक अपने विवेचन में हमने यह मान लिया है कि दाब, आयतन, ताप आदि राशियों में ही परिवर्तन होता है, पदार्थ की मात्रा में कोई परिवर्तन नहीं होता है। अब हम इस बात पर विचार करेंगे कि पदार्थ की मात्रा में परिवर्तन करने से हमारे सूत्रों में क्या परिवर्तन होते हैं। हम किलोग्राम-अणु को पदार्थ की मात्रा में एकक चुनेंगे और निकाय में पदार्थ की मात्रा को इस एकक में द्र (n) श्द्वारा निर्देशित करेंगे। हमारी चर राशियाँ दो प्रकार की हैं। एक वे जिनका मान पदार्थ की मात्रा पर निर्भर नहीं रहता, जैसे ताप अथवा दाब। ये तीव्रात्मक कही जाती हैं। दूसरी प्रकार की राशियों का मान पदार्थ की मात्रा पर निर्भर रहता है, जैसे आयतन तथा एंट्रापी। ये विस्तारात्मक चर राशियाँ कही जाती हैं। इसी प्रकार यदि किसी चुंबकीय पदार्थ को एक चुंबकीय क्षेत्र में रखा जाए तो चुंबकीय क्षेत्र तीव्रात्मक चर राशि होगा और चुंबकीय घूर्ण विस्तारात्मक चर राशि। यदि हम पिछले सूत्रों का निरीक्षण करें तो हम देखेंगे कि प्रत्येक तीव्रात्मक चर राशि एक विस्तारात्मक चर राशि से संबद्ध है। इनको संयुग्मी चर राशियाँ कहते हैं। दाब एवं आयतन संयुग्मी चर राशियाँ हैं। इसी प्रकार ताप और एंट्रापी तथा चुंबकीय क्षेत्र और चुंबकीय घूर्ण संयुग्मी चर राशियाँ हैं।

किसी निकाय की ऊर्जा उसके पदार्थ की मात्रा पर निर्भर रहती है। अतएव निकाय की ऊर्जा में परिवर्तन न केवल उसको गर्म करने अथवा उसपर कार्य करने से होगा, अपितु उसके आयतन तथा एंट्रापी को नियत रखकर उसमें पदार्थ की मात्रा में परिवर्तन करने से भी होगा। यदि आ_१(V), एं_१(S), ऊ_१(u), पू_१(h), फ_१(f), तथा फू_१(g), किसी निकाय के एक किलोग्राम-अणु के क्रमानुसार आयतन, एंट्रापी, ऊर्जा, पूर्णोष्मा, हेल्महोल्ट्स की स्वतंत्र ऊर्जा तथा गिब्ज़ की स्वतंत्र ऊर्जा हैं तो

आ = द्र आ_१, एं = द्र एं_१, ऊ = द्र ऊ_१, पू = द्र पू_१, तथा फू = द्र फू_१, (७४)

श्तथा �� (७४)

एवं ता ऊ = पा ताएं - दा ताआश् + रा ता द्र, (७५)

�� (७५)

ता पू = पा ताएं + आ तापा + रा ता द्र, (७६)

�� (७६)

ता फा = - एं तापा + दा ताआश् + रा ता द्र, (७७)

�� (७७)

ता फू = - एं तापां + आ तादाश् + रा ता द्र। (७८)

�� (७८)

रा (m) को रासायनिक विभव कहते हैं और उपर्युक्त समीकरणों से प्रगट है कि रा (m) तथा द्र (n) संयुग्मी चर राशियाँ हैं। रासायनिक विभव का मान निम्नाकिंत समीकरण से प्रगट है :

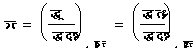
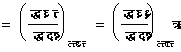(७९)

�� (७९)

उपर्युक्त समीकरण के अंतिम पद से रा (m) का मान तुरंत निकाला जा सकता है।

फू = ऊ - पा एं + दा आ = द्र ऊ ₁- द्र पा एं_१+ द्र दा आ_१

अतएव ताफू = ताद्र (ऊ ₁- द्र पा एं_१+ द्र आ_१) + द्र (ताऊ - एं_१+ तापा

- पा ताएं_१+ दा ताआ_१+आ_१तादा)

= ताद्र (ऊ ₁- पा ताएं_१+ दा आ_१) + द्र (आ_१ तादा - एं_१तापा)

()()

�� ()()

तथा 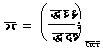= ऊ पा एं_१+ दा आ_१= फू_१) (८०)

�� (८०)

श्

अर्थात् रासायनिक विभव एक किलोग्राम-अणु की गिब्ज़-ऊर्जा के बराबर होता है। समीकरण (८०) तभी ठीक होता है जब निकाय में एक ही तरह का पदार्थ होता हो। यदि निकाय में कई तरह के पदार्थ हों तो समीकरणों (७५), (७६), (७७) एवं (७८) की जगह निम्नलिखित समीकरण होंगे :

ताऊ = पाता एं - दा ता आ + �_चरा_च�ताद्र_च(८१)

�}

तापू = पाता एं + आ तादा + �_चरा_च�ताद्र_च(८२)

�}

ताफा = - एं तापां - दा ताआ + �_चरा_च�ताद्र_च(८३)

�}

ताफू = - एं तापां - आ तादा + �_चरा_च�ताद्र_च(८४)

�}

अतएव ��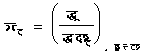

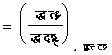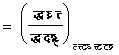
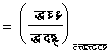�� (८५)

इन समीकरणों से भी मैक्सवेल के संबंधों की तरह संबंध प्राप्त किए जा सकते हैं। उदाहरणत:

�� (८६)

}�� (८६)

समीकरण (८५) के अंतिम समीकरण बहुत महत्वपूर्ण है। यदि किसी निकाय में प्रत्येक प्रकार के पदार्थ की मात्रा दूनी कर दी जाए तो फू का मान भी दूना हो जाएगा। वस्तुत:

फू (ठ द्र_१, ठ द्र_२, . . .) = ठ फू (द्र_१, द्र_२, . . .)। (८७)

() ()�� (८७)

परंतु इसका अर्थ यह है कि फू (G) पदार्थ मात्राओं काएक घात का समघात फलन है। अतएव आयलर के प्रमेय की सहायता से

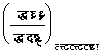
��_चरा_चद्र_च।

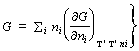�� (८८)

�� = �_im_in_i

समीकरण (८८) के अवकलन से

ताफू = �_चरा_च�ताद्र_च + �_चरा_चद्र_च।

इसमें से समीकरण (८४) को घटाने से

एं तापा - आ तादा+ �_चद्र_चश्तारा_च=०। (८९)

}�� (८९)

समीकरण (८९) गिब्ज़-ड्यूहेम-संबंध कहलाता है।

१०. साम्यावस्था के प्रतिबंध-जितने वास्तविक परिवर्तन होते हैं वे कम स्थायी स्थितियों से अधिक स्थायी स्थितियों की ओर होते हैं। असमताओं (४६), (५०), तथा (५१) को ध्यान में रखते हुए हम इस परिणाम पर पहुँचे हैं कि साम्यावस्था में

निश्चित ऊ (U)श् तथा आ (V)श् के लिए एं (S) अधिकतम होता है। (९०)

निश्चित पू (H) श्तथा दा (P)श् के लिए एं (S) अधिकतम होता है। (९१)

निश्चित पा (T)श् तथा आ (V)श् के लिए फा (F)श् न्यूनतम होता है। (९२)

निश्चत पा (T)श् तथा दा (P)श् के लिए फू (G) न्यूनतम होता है। (९३)

असमता (४६) को ध्यान में रखते हुए (९०) तथा (९१) को दूसरी तरह भी लिखा जा सकता है।

निश्चित एं (S)श् तथा आ (V) के लिए ऊ (U) न्यूनतम होता है। (९४)

निश्चित एं (S) तथा दा (P) के लिए पू (H) न्यूनतम होता है। (९५)

क्योंकि एं (S) की अपेक्षा पा (T) की जानकारी अधिक सुगमता से हो सकती है, अतएव (९४) एवं (९५) की अपेक्षा (९२) तथा (९३) अधिक उपयोगी हैं। यदि पा (T) तथा आ (V) स्वतंत्र चर राशियाँ हैं तो साम्यावस्था में

_श्ताफा _श्= ० । dF = o (९६)

यदि पा तथा दा स्वतंत्र चर राशियाँ हों तो साम्यावस्था में

_श्ताफू _श्= ० । dG = o (९७)

११. आदर्श गैसों के मिश्रण में रासायनिक साम्यावस्था-द्रव्यमात्रा क्रिया नियम-यदि हम दो गैसों को मिलाएँ तो मिश्रण की एंट्रापी वही नहीं होती जो उनकी अलग-अलग एंट्रापियों के जोड़ने से प्राप्त होती है। इसका कारण यह है कि मिलाने पर उन गैसों का पारसरिक विस्तार होता है जो एक अनुत्क्रमणीय परिवर्तन होता है। समीकरण (७३) में थोड़ा परिवर्तन करके हम मिश्रण की एंट्रापी निकाल सकते हैं। मिश्रण का दवाब डाल्टन के नियम के अनुसार

दा = �_च दा_च। �� (९८)

और दा_च = द्र_च झ पा/ आ।

अतएव दा = द्र झ पा/ आ, दा = �द्र_च

�� (९९)

और दा_च = (द्र_च / द्र।) दा। p_i = (n_i/ n) p�� (१००)

अतएव द्र_च एं_च = द्र_च वि_वाच लघु पा - द्र_च झ लघु दा_च + द्र_च एं_च_०

द्र_च { एं_चश् (पा, दा) + �झ लघु (द्र / द्र_च)}�� (१०१)

n_i S_i = C_pi log T- n_i R log P_i + n_i S_io

अतएव = n_i

फू = पू - पाएं

=�_चद्र_च {(पू_१)_च (पा) - पाएं_च (पा दा) - झपा लघु (द्र/द्र_च)

=�_चद्र_च{(फू_१)_च (पा, दा) - झपा लघु (द्र/द्र_च)}�� (१०२)

G = H - T S

�� =�_i n_i

�� =�_i n_i�� (१०२)

समीकरणों (८८) तथा (१००) की तुलना से हम देख सकते हैं कि

रा_च= (फू_१)_चश् - झपा लघु (द्र/द्र_च)।

�� (१०३)

समीकरण (८०) के स्थान पर मिश्रण में रा_च (m₁) तथा (फू_१)_च (g₁) में उपर्युक्त संबंध होता है। अब हम मान लेंगे कि रासायनिक क्रिया किसी विशेष ताप तथा दाब पर होगी। इसलिए साम्यावस्था में ताफू=० (dG=0)। समीकरण (१०२) की सहायता से

ताफू= �_पताद्र_च{(फू_१)_च (पा, दा) - झपा लघु (द्र/द्र_च)। (१०३)

श्- झपा �_चद्र_चता लघु (द्र/द्र_च)

dG = �_i dn_i {g_i (T, p) - RT� log n/n_i}

�- RT� �_i n_i d( log� n/n_i)

उपर्युक्त पदसंहति के अंतिम पद शून्य के बराबर होगा। ताद्र_च (dn₁) उन अणुओं की संख्या के अनुपात में होंगे जो उस रासायनिक क्रिया में भाग ले रहे हैं। यदि इन अणुओं की संख्या सं_१, सं_२, सं_३... (u_1,u_2,u_3,). . .� है तो

�_चसं_चश्{(फू_१)_च (पा, दा) - झपा लघु (द्र/द्र_च) =० (१०४)

�_i u_i{g_i (T, p) - RT� log (n/n_i)}= o�� (१०४)

अथवा

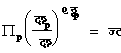�� (१०५)

जहाँ लघु �_चसं_चश्(फू_१)_च (दा, पा)।

�� (१०५)

जहाँ �_i u_i�g_i ( p T )

इस नियम का प्रतिपादन नार्वे के गुल्डबर्ग तथा बाग नामक दो वैज्ञानिकों ने सन् १८६७ ई. किया था। इस समीकरण को आण्विक भिन्नों के रूप में हम यों लिख सकते हैं :

जिसमें �� (१०६)

�जिसमें �� (१०६)

इनश् समीकरणों में वे सं_चश्(u₁) धन होते हैं जो अणु रासायनिक क्रिया के फलस्वरूप उत्पन्न होते हैं और जो लुप्त होते हें वे ऋण होते हैं। समीकरणों (१०५) तथा (५५) की सहायता से

�� (१०७)

इसमें (आ_१)_च (V₁) एक किलोग्राम-अणु का दाब दा (P) पर आयतन। अतएव दा (आ_१)_च =झ पा, (PV₁=RT) तथा

��

अथवा ० (१०८)

o�� (१०८)

समीकरण (१०८) के समाकलन से

�� (१०९)

जिसमें गश् (C) दाब के ऊपर निर्भर नहीं रहता। समीकरण (१०६) में

ग_च = द्र_च/द्र = दा_च/दा। (Ci = n_i/n = p_i/p)

अतएव P_चश्(दा_च/दा) सं^च= ट। [P_i( p_i/p) ui = K ]

अर्थात् त_दा= P_चदा_चसं^च= ट दा �_चसं^च= ग। (११०)

श्K = P_i�p_i�V_i = K p�ⁱ ui = C�� (११०)

इससे प्रकट है कि ट_दाश्(K_P) दबाव पर निर्भर नहीं है।

इसी प्रकार समीकरणों (१०५) तथा (५५) की सहायता से

श्

�� (१११)

��

�� (१११)

समीकरण (१०५), (१०७) तथा (१११) बहुत महत्वपूर्ण हैं। समीकरण (१०५) से यह स्पष्ट है कि ट (K) के मान में वृद्धि होने से उन संघटनों के सांद्रण में वृद्धि होती है जिनके संश् (u₁) धन होते हैं। समीकरण (१०७) से यह स्पष्टश् है कि ताप को निश्चित रखते हुए दाब में वृद्धि की जाए तो रासायनिक क्रिया उस ओर चलेगी जिधर आयतन में कमी होगी। इसी प्रकार समीकरण (१११) से यह स्पष्ट है कि दाब को निश्चित रखते हुए ताप में वृद्धि हो तो रासायनिक क्रिया उस ओर चलेगी जिधर संघटकों में अधिक उष्मा होगी। इस प्रकार समीकरण (१०७) तथा (१११) एक बहुत व्यापक नियम को स्पष्ट करते हैं जिसे लशाटल्ये-नियम कहते हैं और जो यह है :

''यदि किसी उष्मागतिकी निकाय की बाह्य अवस्थाओं में परिवर्तन किया जाए तो निकाय की साम्यावस्था उस दिशा में परिवर्तित होगी जिससे बाह्य परिवर्तनों के मानों में कमी होगी।''

१२. क्लाजिउस-क्लेपिराँ-समीकरण तथा पानी का बिंदु-अब हम इस बात पर विचार करेंगे कि यदि कोई संघटन गैस, द्रव आदि कई कलाओं (फ़ेज़ेज़) में किसी निकाय में हो तो इन कलाओं में पारस्परिक संबंध क्या होता है। यदि संघटक गैस तथा द्रव दो अवस्थाओं में हो और निकाय में इसकी कुल द्रव्यमात्रा नियत हो तो

द्र = द्र_गैस+ द्र _द्रव। (n = n_गैस�+ n_द्रव) �� (112)

जिसमेंश् द्र_गैस(n_गैस) तथा द्र _द्रव( n_द्रव) किलोग्राम-अणु एककों में गैस तथा द्रव अवस्थाओं में निकाय में विद्यमान संघटक की मात्रा हैं। अतएव

d द्र_गैस+ d द्र _द्रव= ०।श् ( d n_गैस�+ d n_द्रव= ०) �� (113)

इसी प्रकार फू = (फू_१) _गैस+ द्र_द्रव(फू_१) _द्रव �� (114)

�� G = n_गैस(g)_गैस+ n_द्रव(g)_द्रव �� (114)

ताप तथा दाब को नियत रखकर साम्यावस्था में

d फू+ d द्र_गैस_श्(फू_१) _गैस + d श्द्र_द्रव_श्(फू_१) _द्रव। �� (115)

�� dG+ d n_गैस(g)_गैस + d n_द्रव_श्श्(फू_१) (g)_द्रव �� (115)

समीकरणों (११३) तथा (११४) के कारण

(फू_१) _गैस(पा, दा) = (फू_१) _द्रव (पा, दा)। (116)

�� (g)_गैस (T, P) = (g)_द्रव(T, P)�� (116)

यदि हम पानी तथा उसके वाष्प की साम्यावस्था का अध्ययन कर रहे हैं तो हम गैस के स्थान पर भाप एवं द्रव के स्थान पर जल लिखेंगे। यदि हम ताप को पा (T) से पा + तापा (T+dT) करें जिससे संतृप्त भाप की दाब दा + तादा (P+dP) हो जाए तो

(फू_१)_भाप�(पा + तापा, दा + तादा) = (फू_१)_जल(पा + तापा, दा + तादा) (117)

�� g_भाप(T + dT, p + dp) g_जलश्(T + dT, p + dp)�� (117)

परंतु फू (पा + तापा, दा + तादा)

= (फू_१) (पा, दा) + ता दा + तापा

= (फू_१) (पा, दा) - एं तादा + आ तापा। (118)

�� g (T + dT, p + dp) = g (T,� p) =

�� = g (T,� p) - S dp + V dT

श्

अतएव समीकरणों (११६), (११७) तथा (११८) की सहायता से

- एं_भापश्तापा + आ_भापता दा = - एं_जलश्तापा + आ_जलता दा,

- S_भाप dT + V_भाप�dp = - S_जलdT + V_जल dp

अर्थात् संतृप्ति

�� (119)

संतृप्ति

जिसमें गु = पा (एं_भाप- एं_जल)

[L = T (S_भाप- S_जल)] = पानी की गुप्त उष्मा

समीकरण (११९) क्लाज़िउस-क्लेपिराँ-समीकरण कहलाता है। इसे समीकरण (५८) में दिए मैक्सवेल के संबंध से भी स्थापित किया जा सकता है, परंतु उपर्युक्त प्रतिपादन अधिक संतोषजनक है।

यदि किसी निकाय में पानी ठोस, तरल एंव गैस इन तीनों ही अवस्थाओं में वर्तमान हो तो समीकरण (११६) की भांति हम यह सिद्ध कर सकते हैं कि

(फू_१)_हिम= (फू_१)_जल। �g_हिम=�g_जल(१२०)

एवं (फू_१)_हिम= (फू_१)_भाप। (g_हिम=�g_भाप)(१२१)

परंतु (१२०) तथा (१२१) समीकरणों का अर्थ हैं-

(फू_१)_जल= (फू_१)_भाप।श् (g_जल=�g_भाप)(१२२)

और निर्देशांक ज्यामिति के एक प्रमय के अनुसार समीकरण (१२२) का वक्र समीकरणों (१२०) एवं (१२१) के वक्रों के उभयनिष्ठ बिंदु से होकर गुजरेगा। इस बिंदु को पानी का त्रिगुण बिंदु कहते हैं।

समीकरण (११९) द्वारा यह ज्ञात किया जा सकता है कि ताप बढ़ने से संतृप्त भाप की दाब कितनी बढ़ती है। हिम तथा पानी की साम्यावस्था से भी इसी तरह का समीकरण निकाला जा सकता है, जिसके द्वारा यह ज्ञात किया जा सकता है कि दाब से गलनांक में क्या परिवर्तन होता है।

१३. गिब्ज़ का कला नियम-ऊपर हमने यह मान लिया है कि निकाय में एक ही प्रकार का संघटक है। अब हम कल्पना करेंगे कि संघटकों की संख्या १, २. . ., स के बराबर है तथा कलाओं की संख्या १, २. . .क के बराबर है। अतएव पूरे निकाय के लिए

�� (१२३)

इसमें (फू_१)च_छ [g_jj] संघटक च (i) का कला छ ( j ) में गिब्ज़ की स्वतंत्र ऊर्जा प्रति किलोग्राम-अणु है तथा द्र_चछ(n _ij) निकाय में इसके किलोग्राम-अणुओं की संख्या है। साम्यावस्था में फू =० (G=0 ) होता है अतएव

० (१२४)

0�� (१२४)

परंतु प्रत्येक संघटता की मात्रा नियत है। अतएव

०, च =१, २, . . . स। (१२५)

i=1, 2, . . . स। (१२५)

समीकरणों (१२४) तथा (१२५) से लाग्रांज के अनिर्धारित गुणांक विधि की सहायता से

(फू_१)_च१= (फू_१)_च२. . .= (फू_१)_चफ'। च=1, 2, 3,... ।(१२६)

g_i1 = g_i2 . . . = g _i_फ ' i = 1, 2, . . .� स

समीकरण (१२६) में समीकरणों की कुल संख्या स (क-१) है। अब हम चर राशियों की संख्या पर विचार करेंगे। साम्यावस्था में प्रत्येक कला में संघटकों के अनुपातों का ही महत्व है। अतएव इन चर राशियों की संख्या क (स-१) है। इनमें ताप तथा दाब को मिलाने से चर राशियों की कुल संख्या क (स-१) + २ है। इन राशियों पर समीकरण (१२६) द्वारा निर्देशित स (क-१) प्रतिबंध हैं। यदि स्वतंत्र चर राशियों की संख्या म हैं तो

म = क (स-१) + २ - स (क-१)

= स - क + २; (१२७)

अर्थात् म + क = स + २। (१२८)

समीकरण (१२७) अथवा (१२८) गिब्ज़ के कलानियम को प्रकट करते हैं। निकाय की मुक्तता की कोटि म, कलाओं की संख्या क तथा संघटकों की संख्या स में उपर्युक्त समीकरण होते हैं।

१४. उष्मागतिकी के द्वितीय सिद्धांत के अन्य उपयोग-उष्मागतिकी के द्वितीय सिद्धांत के जो उपयोग ऊपर दिए गए हैं उनके अतिरिक्त इसके और भी उपयोग हैं जिनका विवेचन स्थानाभाव के कारण नहीं किया जा सकता। उदाहरणत:, तनु विलयनों के रसाकर्षणीय दाब, विलयनों में रासायनिक साम्यावस्था, विलायक एवं विलयन की वाष्पदाबों के अंतर, द्रवों द्वारा गैसों के अवशोषण, चुंबकीय क्षेत्र में चुंबकीय पदार्थों की विशिष्ट उष्मा आदि के अध्ययन के लिए स्थिरोष्म अचुंबकनविधि (ऐडियाबैटिक डीमैग्नेटिज़ेशन) का उपयोग किया जाता है। इसका भी अध्ययन उष्मागतिकी द्वारा किया जा सकता है। इसके अतिरिक्त समीकरण (६१) की सहायता से यह सिद्ध किया जा सकता है कि गैल्वनीय कोशिकाओं का विद्युद्वाहक बल निम्नलिखित समीकरण से प्रकट किया जा सकता है :

द्यु - पा�� (129)

�� (129)

जिसमें द्यु (E ) कोशिका का विद्युद्वाहक बल है, श्ऊ ( V ) रासायनिक क्रिया में प्राप्त उष्मा है, यो (Z ) संयोजकता है, तथा फै (F ) फैराडे संख्या है।

१५. उष्मागतिकी का तृतीय सिद्धांत-यांत्रिकी के अध्ययन से दाब तथा आयतन के साथ हमारा परिचय होता है। उष्मागतिकी के शून्यवें सिद्धांत से ताप, प्रथम सिद्धांत से उष्मा एवं द्वितीय सिद्धांत से एंट्रापी, स्वंतत्र ऊर्जा आदि निकाय की विशिष्टताओं का समावेश होता है। तृतीय सिद्धांत द्वारा किसी नई विशिष्टता का समावेश नहीं होता। इसके द्वारा केवल एं (U ), फा श्(E ), फू श्(G ) आदि का मान निश्चित हो जाता है।

यदि किसी रासायनिक क्रिया में ऊ (U ) तथा फा (E ) में परिवर्तन क्रमश: श्ऊ ( U ) तथा श्फा ( F ) हो तो समीकरण (६१) के अनुसार

�� (130)

नेर्न्स्ट ने यह देखा कि प्राय: रासायनिक क्रियाओं में श्ऊ तथा श्फा ( U� तथा �F ) में बहुत कम अंतर होता है। इसका कारण यह है कि त ( फा/त पा श्का मान बहुत कम होता है।

अतएव नेर्न्स्ट ने यह सिद्धांत रखा कि ज्यों-ज्यों हम परमशून्य ताप की ओर बढ़ते हैं त्यों-त्यों त (फा) तपा श्का मान कम होता जाता है और परमशून्य ताप पर इसका मान शून्य के बराबर होगा। समीकरण (१३०) के अनुसार परमशून्य ताप पर यदि त ( फा)/तफा [� ( F ) [� T )का मान कोई परिमित संख्या हो तो श्ऊ ( U� तथा फा ( F ) तथा फा एक दूसरे के बराबर होंगे। परंतु नेर्न्स्ट के सिद्धांत के अनुसार

सीमासीमा, (131)

�� (131)

क्योंकि समीकरण (१३०) के अवकलन से

यदि ।

�� , यदि

क्योंकि एं,

अतएव समीकरण (१३१) का अर्थ यह है कि परमशून्य ताप परएं =० (S= o)। यह सिद्धांत नेर्न्स्ट ने सन् १९०६ ई. में प्रतिपादित किया था। इसके पश्चात् प्लांक ने सन् १९१२ ई. में यह कहा कि परमशून्य ताप पर न केवल एं =० (S= o), अपितु एं =० (S= o)। तृतीय सिद्धांत को कभी-कभी नेर्न्स्ट का उष्मा प्रमेय भी कहते हैं।

१६. तृतीय सिद्धांत के उपयोग-तृतीय सिद्धांत द्वारा यह सिद्ध किया जा सकता है कि परमशून्य ताप पर प्रसरण गुणांक शून्य के बराबर होता है तथा ताप के साथ दाब के बढ़ने का गुणांक भी शून्य के बराबर होता है। इसी प्रकार यह भी सिद्ध किया जा सकता है कि परमशून्य ताप पर, नियत दाब पर तथा नियत आयतन पर विशिष्ट उष्माएँ वि_दा (C_p) तथा वि_आ(C_y) दोनों ही शून्य के बराबर होती हैं। परंतु सबसे महत्वपूर्ण परिणाम यह है कि किसी भौतिक क्रिया द्वारा परमशून्य ताप पर पहुँचना असंभव है। हम जानते हैं कि निम्न ताप पर ताप कम करने की सबसे अच्छी विधि स्थिरोष्म विचुंबन (ऐडियाबैटिक डीमैग्नेटिजेशन) है। परंतु हम सिद्ध कर सकते हैं कि इस विधि से भी परमशून्य ताप पर पहुँचना असंभव है। इसके लिए हम पा - एं (T-S) रेखाचित्र में निकाय की अवस्था का निर्देशन करेंगे। यह चित्र ५ में किया गया है।

श्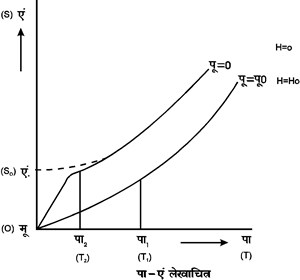

चित्र ५ पा-एं लेखाचित्र

नियत ताप पर चुंबकीय पिंड को चुंबकीय क्षेत्र में रखने से संट्रापी कम हो जाती है जैसा इस रेखाचित्र में पू(H) एवं पूपू_०(HH_०) के वक्रों द्वारा दिखाया गया है। इस रेखाचित्र द्वारा हम देख सकते हैं कि यदि ताप पा_१ (T₁) तथा पूपू_०(HH_०) से चुंबकीय क्षेत्र शून्य कर दें तो हम ताप पा_२(T₂) पर पहुँचेंगे।

ताप पा_२(T₂) ऐसा है कि पू(H) की अवस्था में एंट्रापी का वही मान है जो ताप पा१ पर अवस्था पू में। यदि शून्य ताप पर एंट्रापी शून्य होकर एं_०(S_०) के बराबर होती तो हम शून्य ताप पर पहुँचे सकते, परंतु तृतीय सिद्धांत के अनुसार यह असंभव है।

१७. द्वितीय सिद्धांत का स्वयंताथ्यिक प्रतिपादन-ऊपर हमने द्वितीय सिद्धांत का प्रतिपादन किया है जो क्लाजिउस आदि के अनुसार है। इसके अतिरिक्त कैराथियोडोरी ने स्वयंताथ्यिक प्रतिपादन दिया है। कैराथियोडोरी का प्रमेय यह है कि दा-आ (p-V) लेखाचित्र में निकाय की अवस्था में निर्देश बिंदु के आसपास ऐसे अनेक बिंदु हैं जिन तक उत्क्रमणीय-स्थिरोष्म-प्रक्रम द्वारा पहुँचना असंभव है। इस प्रमेय से आरंभ करके परमताप एवं एंट्रापी की भावना तक पहुँचा जा सकता है।

��.O��-गुगेनहाइम : थर्मोडाइनैमिक्स; विल्सन : थर्मोडाइनैमिक्स ऐंड स्टैटिस्टिकल मिकैनिक्स; सोमरफ़ेल्ड : थर्मोडाइनैमिक्स ऐंड स्टैटिस्टिकल मिकैनिक्ल मिकैनिक्स; फर्मी : थर्मोडाइनैमिक्स।

�