इलेक्ट्रान पदार्थ का मूलभूत कण है। इलेक्ट्रान की संख्या और इलेक्ट्रानिकों संरचना पर ही पदार्थ के कई भौतिक और रासायनिक गुणधर्म निर्भर करते हैं। १८७९ में एक अंग्रेज भौतिकशास्त्री सर जे. जे. थामसन ने इस ऋण आवेशयुक्त कण की खोज की और सिद्ध किया कि यह प्रत्येक परमाणु का एक अनिवार्य भाग है। प्रत्येक परमाणु आवेशहीन होता है अत: थामसन ने निष्कर्ष निकाला कि इलेकट्रान के ऋण आवेश के बराबर परमाणु धन आवेश का एक गोला है जिसमें ऋण आवेश बिखरा रहता है (जैसे तरबूज में बीज)। उनके प्रयोगों से पता चला कि परमाणु का भार इलेक्ट्रान के भार से बहुत ज्यादा है, अत: उन्होंने कल्पना की कि परमाणु का भार मुख्य रूप से धन आवेश के कारण होता है।
कुछ साल बाद लार्ड रदरफोर्ड ने पाया कि थामसन का 'परमाणु रूपक स्वर्णपत्र द्वारा अल्फा कणों के प्रायोगिक विक्षेपण के निष्कर्षो की व्याख्या नहीं करता अत: १९११ में रदरफोर्ड ने परिकल्पना की कि धन आवेश परमाणु में केंद्र के पास थोड़े से आयतन नाभिक में केंद्रित रहता है और इलेक्ट्रान नाभिक के चारों ओर सौरमंडल के ग्रहों के समान घूमते रहते हैं पर ऐसे परमाणु में घूमनेवाले इलेक्ट्रान नाभिक की तरफ निरंतर त्वरित होंगे अत: निरंतर ऊर्जा उत्सर्जित करते हुए इन्हें नाभिक के और पास आना चाहिए। पर प्रयोग इसका समर्थन नहीं करते।
१९१३ में डेनमार्क के एक भौतिकविद् नील्स बोहर ने आइन्स्टीन के 'कैसे एक निश्चित ऊर्जावाला प्रकाश पदार्थो में से इलेक्ट्रान उत्सर्जन करता है' की व्याख्या से प्रभावित होकर प्रतिपादित किया कि परमाणु में इलेक्ट्रान केवल निश्चित वृत्ताकार कक्षों में ही गमन कर सकते हैं।
बोहर ने माना कि जब तक इलेक्ट्रान इन संभव कक्षों में से किसी एक में गमन करते रहते हैं, वे ऊर्जा विकीरित नहीं करते। पर यदि इलेक्ट्रान एक बाहरी कक्ष से नाभिक के पासवाले कक्ष में गमन करें तो प्रकाश के रूप में ऊर्जा उत्सर्जित करते हैं। यह उत्सर्जित ऊर्जा इन कक्षों के ऊर्जा अंतर के बराबर होगी। किसी कक्ष की ऊर्जा इस कक्ष के अर्धव्यास पर निर्भर करती है। और कक्ष का अर्धव्यास नाभिक के धन आवेश द्वारा कक्ष के इलेक्ट्रान पर लगे आकर्षण बल के प्रभाव को नष्ट करने के लिए आवश्यक केंद्रापसारी बल द्वारा निर्धारित होता है। यह केंद्रापसारी बल कक्ष में इलेक्ट्रान की गति से उत्पन्न होता है।
बोहर के प्रतिपादन के पश्चात् हुए प्रायोगिक और सैद्धांतिक कार्यो से ज्ञात हुआ कि वास्तव में इलेक्ट्रान का पूरी तरह ज्ञात कोई एक कक्ष नहीं होता परंतु इलेक्ट्रान नाभिक के चारों ओर फूले हुए कार के टयूब की आकृतिवाले क्षेत्र में गमन करता रहता है--कभी नाभिक के पास, कभी दूर। यह गति वास्तव में नाभिक के चारों ओर एक फूले हुए टयूब की आकृतिवाले ऋण आवेश के वलय का निर्माण करती है। इसे इलेक्ट्रान बादल के नाम से भी जाना जाता है।
हालाँकि इलेक्ट्रान बादल में रहते हैं पर एक साधारण आवेशहीन परमाणु में इलेक्ट्रान के बोहर द्वारा प्रतिपादित कक्षों में से किसी एक में पाए जाने की संभावना ही सबसे अधिक है।
आजकल कक्ष का अर्थ उस सारे क्षेत्र से लिया जाता है जिसमें इलेक्ट्रान गमन करता है, न कि पूरी तरह निश्चिम एक वृत्त से। १९२५ में पाली ने प्रतिपादित किया कि एक ही परमाणु से कोई भी दो इलेक्ट्रान एक ही समय एक ही अवस्था (क्वांटम अवस्था) में नहीं रह सकते हैं। यह पाली का विस्थापन सिद्धांत कहलाता है। किसी इलेक्ट्रान की क्वांटम अवस्था चार अंकों द्वारा प्रदर्शित की जाती है। इनमें से पहला अंक इलेक्ट्रान के कक्ष का अर्धव्यास निश्चित करता है और अन्य तीन चक्रीय घूर्ण (रोटेशनल मोमेंटम्)।
समान ऊर्जावाले सभी इलेक्ट्रान एक ही क्षेत्र में स्थित कक्षीय अनुक्रमों में गमन करते हैं। इन अनुक्रमों को शेल कहते हैं। इनमें नाभिक के सबसे पासवाले शेल को K शेल कहते हैं और इसकी ऊर्जा सबसे अधिक होती है। L शेल की ऊर्जा K से कम और अन्य सभी M], N] आदि शेलों से अधिक होती है। यह K शेल की अपेक्षा नाभिक से दूर होता है। इसी प्रकार M की ऊर्जा Kऔर L शेल की ऊर्जा से कम और अन्य शेलों की ऊर्जा से ज्यादा होती है। विशेष जानकारी के लिए द्र. 'परमाणु'। (म.त्रि.)
आवेश आदि-यदि हम दो विद्यदग्रों (इलेक्ट्रोडों) को एक ऐसी बंद नली में रखें जिसमें से हवा निकाल दी गई हो (दाब पारे का १०-३ मि. मी.) तो, विभव (पोटेंशियल) लगाने पर, ऋणाग्र में से प्राय: एक नीली सी धारा निकलती दिखाई पड़ती है। यदि नली को चुंबकीय अथवा वैद्युत क्षेत्र में रखें तो यह धारा इधर उधर मोड़ी जा सकती है। मोड़ की दिशा से पता चलता है कि यह धारा ऋण आवेश (नेगेटिव चार्ज) के कणों की बनी हुई है। जैसा ऊपर बताया गया है, इन कणों को इलेक्ट्रान कहते हैं। वास्तव में, यदि इन क्षेत्रों का परिमाण ज्ञात हो तो, धारा का विक्षेप नापने से इन कणों के आवेश तथा द्रव्यमान ज्ञात हो सकते हैं। इन प्रयोगों का परिणाम यह है कि इलेक्ट्रान के आवेश आदि निन्मलिखित के अनुसार हैं:
आवेश (आ) =(१.६०२०३३±०.०००३४)´१०-२० निरपेक्ष वैद्युत चुंबकीय एकक,
=(४.८०२५१ ±०.००१०)´१०-१० निरपेक्ष स्थिर वैद्युत एकक,
विशिष्टावेश (आ/द्र) =(१.७५९२±०.००५)´१०७ नि.वैचु./ग्रा,
=(५.२७६६±०.००१५)´१०१७ नि.स्थि./ग्रा१
द्रव्यमान (द्र) =(९.१०६६०±०.००३२)´१०-२८ ग्रा, जहाँ ग्रा=ग्राम।
क्वांटम यांत्रिकी के विख्यात सिद्धांतों के अनुसार इलेक्ट्रान के साथ हम एक तरंग का भी अनुमान कर सकते हैं। यदि इलेक्ट्रान का संवेग सं है तो उसका तरंगदैर्ध्य दै=प्ल/सं (l=l mv) होगा। (द्र क्वांटम यांत्रिकी), जहाँ प्ल प्लांक का नियतांक है। अत: प्रकाश अथवा एक्सरश्मि की जगह हम इलेक्ट्रान का भी प्रयोग कर सकते हैं। इस आधार पर इलेक्ट्रान सूक्ष्मदर्शी बने हैं, जो वैज्ञानिक अन्वेषणों में बहुत लाभकारी सिद्ध हुए हैं। (द्र. इलेक्ट्रान सूक्ष्मदर्शी)। साधारण तालों की जगह इनमें वैद्युत तथा चुंबकीय क्षेत्रों का प्रयोग होता है।
वर्तमान शताब्दी के वैज्ञानिक तथा औद्योगिक विकास में इलेक्ट्रान का अत्यंत महत्वपूर्ण स्थान रहा है। पिछले वर्षों में और भी बहुत से कण मिले हैं, पर वे अस्थायी हैं।
डिरैक समीकरण---इलेक्ट्रान के विवरण के लिए डिरैक समीकरण का उपयोग आवश्यक है (द्र डिरैक)। जैसा क्वांटम यांत्रिकी में कहा गया है
आपेक्षिकतानुकूल समीकरणों में सबसे सरल समीकरण निम्नलिखित है:
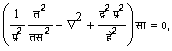
जहाँ प्र=प्रकाश का वेग; स=समय त/तय=¶|¶ c हे=एक नियतांक; सा=Y= इलेक्ट्रान का तरंगफलन (वेव फ़ंक्शन)।
यदि इस समीरण को कारक त/तस त/तय एकघातीय (लीनियर) बनाएँ तो इसका रूप निम्नलिखित हो जाएगा:
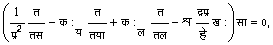
जहाँ श्र=Ö(-१)।
समीकरण (२) से पुन: (१) पाने के लिए यह आवश्यक है कि क:य, क:र, क:ल, ख: साधारण संख्याएँ नहीं, किंतु प्रबंधिनियाँ (मेट्रिसें) हों जो निम्नलिखित दिक्परिवर्तन (कम्युटेशन) नियम का प्रतिपालन करें।
क:य१=क:र२=क:ल२=ख:२=१
क:यक:र+क:रक:य=क:रक:ल+क:ल क:र=क:लक:य+क:यकल=° . . . (३)
तब सा को भी स्तंभप्रबंधिनी (कॉलम मैट्रिक्स) लेना होगा :
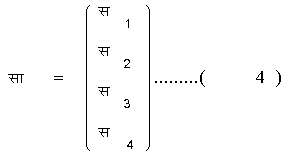
रेखात्मक समीकरण (२) का समावेश करते समय डिरैक ने जो तर्क दिए थे वे अब पूर्णतया न्यायसंगत नहीं माने जाते पंरतु इसमें संदेह नहीं कि इलेक्ट्रान के लिए (२) ही उचित समीकरण है। भौतिकज्ञों को आजकल चुंबकीय समीकरणों की सत्यता में।
प्रबंधिनियाँ क:य, क:र, क:ल, ख: प्रकट रूप से इस प्रकार लिखी जा सकती हैं:
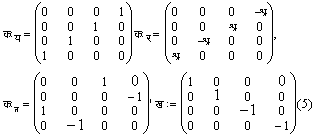
प्रत्यक्ष है कि समीकरण (२) वास्तव में चार युगपत (साइमल्टेनियस) समीकरणों के तुल्य है। सा के घटक (कंपोनेंट) परावर्तन (रिफ्लेक्शन) तथा घूर्णन (रोटेशन) रूपांतरों के प्रति किसी बहुदिष्ट (टेंसर) की तरह आचरण नहीं करते, किंतु आवर्तकों (स्पिनरों) की तरह करते हैं।
ग:-प्रबंधिनियाँ और संकेतन (लेखनपद्धति)--यदि क:य, क:र, क:ल, ख: की जगह हम ग:म (म=१, २, ३) का समावेश करें, जहाँ
ग:0 ख:, ग:१=ख:कय, ग:२= ख:क:र, ग:३= ख:य:ल, . . . (६)
तो (२) को श्रख: से गुणा करने पर उसे इस प्रकार लिख सकते हैं :
![]()
यहाँ अनुबंधनों (सिफ़क्सों) पर योग का प्रचलित नियम (समेशन कनवेंशन) बरता गया है : यदि कोई अनुबंध एक बार नीचे आए और एक बार ऊपर तो उसपर योग होगा। हम विसर्गयुक्त अनुबंधों का ० से ३ तक मान देने के लिए प्रयोग करेंगे और साधारण अनुबंधों को १ से ३ तक मान देने के लिए। (७) में
य०= प्रस, य१=य, य२=र, य३=ल। . . . (८)
अनुबंधों को ऊपर नीचे मापनी (मैट्रिक्स) जमन की सहायता करेंगे :
ज००=१, ज११=ज:२=ज३३=-१, जमन=0(म¹न)। . . . (९)
समीकरणों को सरल बनाने के लिए हम हे और प्र दोनों को इकाई के बराबर मान लेंगे। तब (७) हो जाएगा:
![]()
निरूपण (५) से स्पष्ट है कि ख:, क:ब इत्यादि हमीटियन प्रबंधिनियाँ हैं (द्र क्वांटम यांत्रिकी) :
ख:*=ख, क:प*=क:य,क:र*=क:र,क:ल*=क:ल। . . . (११)
(६) से परिभाषित ग:-प्रबंधिनियाँ में ग: हर्मीटियन है, किंतु ग:१, ग:२, ग:३ विपरीत हर्मीटियन (ऐंटी-होर्मीटियन) हैं :
ग:०*=ग:०, ग:१*=-ग:१, ग:२*=-ग:२, ग:३*=-ग:३। . . . (१२)
ग:म के दिक्परिवर्तन नियम हैं :
ग:मग: न+ ग:नग:म=२जमन . . . (१३)
जहाँ जमन प्रबंधिनी जमन की प्रतिलोम (इनवर्स) है।
यदि हम (१०) पर बाईं ओर से कारक

द्वारा क्रिया करें और (१३) बरतें तो हम पाएँगे कि सा के सब घटक दूसरे घात (आर्डर) के समीकरण (१) को मानते हैं।
आपेक्षिकतानुकूल अचरता (रिलेटिविस्टिक इनवेरियेंस)---समीकरण (१०) को आपेक्षिकतानुकूल सिद्ध करने के लिए हम दिखाएँगे कि यदि हम यस का रूपांतर
यम'= कम यन . . . (१४)
जमन कसक: जसख: कक:ख: . . . (१५)
करें तो साथ ही हम एक ऐसी प्रबंधिनी, ला:, भी ज्ञात करते सकते हैं जो नए अक्षों के तरंगफलन सा¢ को पुराने फलन से समीकरण
सा¢=ला:सा . . . (१६)
द्वारा संबंधित करे और सा' वैसा ही समीकरण संतुष्ट करे जैसा सा¢, अर्थात्
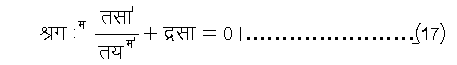
यदि (१०) में हम रूपांतरण (१४) और (१६) करें तो वह

(ला: द्वारा बाईं ओर से गुणा करने पर)।
यहाँ हमने माना है कि ला: निर्देशांक यम' पर निर्भर नहीं है। यह समीकरण (१७) के समान तब होगा जब
कनमला: ग:म ला:-१=ग:न। . . . (१८)
कनक: से गुणा और (१५) का उपयोग करने पर यह हो जाएगा
ला: ग:क : ला:-१= ग:ख : कख : क:। . . . (१९)
यदि (१४) की जगह सूक्ष्म रूपांतर (इनफ़िनिटेसिमल रूपांतर)
कमन=डमन+ ढमन,
ढमन= - ढनम, . . . (२०)
करें तो ला: को तुरंत ही ज्ञात कर सकते हैं। ऐसे रूपांतरों के लिए हम ला: को यों लिख सकते हैं :
ला:=1 +1/2 ढमनटामन, . . . (२१)
टामन=-टानम।
तब (१९) से
1/2ढमन(टामम ग:क:-ग:क:टामन)=गख: ढख: क:,
अर्थात् 1/2ढमन(टामन ग:क:-ग:क:टामन-जक:न-जक.मग:न)=0]
अर्थात् टामन ग:क-ग:क:टामन=जक:नग:न-जक.मग:न . . . (२२)
यदि हम टामन =1/4(ग:म:ग:न - ग:नग:म)º 1/2 ग:(म्ान) . . . (२३)
रख दें तो (२२) संतुष्ट हो जाएगा। क्योंकि सतत रूपांतर बहुत से सूक्ष्म रूपांतरों को जोड़कर बनाए जा सकते हैं, इसलिए स्पष्ट है कि डिरैक समीकरण (१०) आपेक्षिकतानुकूल रूपांतर (१४) के प्रति अचर है। यह भी स्पष्ट है कि सा का रूपांतर (१६) बहुदिष्टों के रूपांतर से भिन्न है।
बहुदिष्ट (टेंसर)-समीकरण (१०) से हम सा के हर्मीटियन संबंध सा*, के लिए समीकरण ज्ञात कर सकते हैं। (१२) का उपयोग करने पर

वह होगा। यदि दाईं ओर ग:० से गुणा करें और सा* की जगह
सा+= सा*ग:० . . . (२४)
काम में लाएँ, तो सा+ यह समीकरण संतुष्ट करेगा :
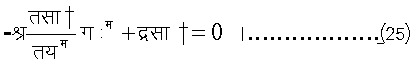
यदि रूपांतर (१४) और (१६) करने पर सा+
सा+'= सा+ला:-१ . . . (२६)
हो जाए, तो समीकरण (२५) अचर रहेगा।
(१६) और (२६) को गुणा करने पर हम देखते हैं कि
सा+¢ सा¢= सा+ सा:। . . . (२७)
अत: सा+सा अचर है।
यदि (१८) की बाईं ओर को सा+¢ द्वारा और दाईं ओर को सा¢ द्वारा गुणा करें तथा (१६) और (२६) के अनुसार ला:-१ सा¢ की जगह सा और सा+¢ ला: की जगह सा+¢ रख दें तो हमें मिलेगा :
कनम्ासा+ गा:म सा = सा+¢गा:नसा¢।
इससे स्पष्ट है कि सा+गा:म सा एकदिष्ट है।
ग:र: के लिए वैसे ही संबध (१८) को
क:र:स:ला: ग:स: ला:-१= ग:र:
से गुणा करने पर हमें मिलेंगे :
क:र:स्ा:कलक:ला: ग:स:ग:कला:-१ = ग:र:ग:न:।
इससे विदित है कि (२८) की तरह फिर
क:र:कक:नखा सा+ ग:कग:ख:सा = सा+¢ग:र सा¢। . . . (२९)
अत: सा+ग:क:सा दूसरी श्रेणी (रैंक) का बहुदिष्ट है। उसे हम एक सममित (सिमेट्रिकल) और एक असममित (ऐंटीसिमेट्रिकल) भागों में विभाजित कर सकते हैं :
ग:क:ग:ख:= 1/2 (ग:क:ग:ख:+ग:ख:ग:क:) +1/2 (ग:क:ग:ख:-ग:ख:ग:क:)=जक:ख:+ग:(क:ख:), (३०)
(देखिए (१३) और (२३)। इनमें जक:ख: तुच्छ है; अत: सा+ग:(ख:क:) सा ही महत्वपूर्ण असममित बहुदिष्ट है।
भौतिकी में ये बहुदिष्ट अत्यंत महत्वपूर्ण हैं। इसलिए हम इस प्रकार की सब संभावनाओं को यहाँ लिखे देते हैं :
अदिष्ट शा = सा+ सा,
एकदिष्ट झम= सा+ ग:न सा,
दूसरी श्रेणी का बहुदिष्ट मामन = श्रसा+ ग:(मन) सा,
तीसरी श्रेणी का बहुदिष्ट (या मिथ्या एकदिष्ट) वामनच=सा+ग:(मनच) सा चौथी श्रेणी का बहुदिष्ट (या मिथ्यादिष्ट)
पामनचछ=श्रसा+ग:(मनचछ) सा। . . . (३१)
ग:[मनच]= 1/6(ग:मग:नग:च - ग:नग:चग:म + ग:नग:चग:म - ग:नग:मग:च +
ग:चग:मग:न - ग:चग:नग:म,
ग:[मनचछ]= 1/24 (ग:मग:नग:चग:छ - ग:म्ाग:नग:छग:च +) (इत्यादि)
~ग: (५)
विद्युच्चुंबकीय अंत: प्रभाव-यदि इलेक्ट्रान और विद्युतच्चुबंकीय क्षेत्र के बीच अंत:प्रभाव भी (१०) में सम्मिलित करें तो वह

से भी प्राप्त हो सकते हैं। (३५) के प्रथम पद को हम आवेश अत: प्रभाव कह सकते हैं। द्वितीय पद दूसरे घात का है। यदि हम प्रतिबिंब
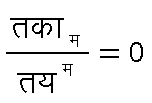
लगाएँ तो तृतीय पद शून्य हो जाएगा। चर्तुर्थ पद एक नया प्रभाव निर्दिष्ट करता है जो (३६) से नहीं आ सकता। यह विद्युच्चंबुकीय क्षेत्र की तीव्रता, फा मन, का समानुपाती है। अत: हम इसको इलेक्ट्रान के चुंबकीय घूर्ण (मैगनेटिक मोमेंट) के साथ अंत: प्रभाव का अर्थ दे सकते हैं। यह सच है कि इस पद में न केवल चुंबकीय, किंतु वैद्युत क्षेत्र भी संमिलित है। चुबंकीय और वैद्युत क्षेत्रों का साथ साथ आना आपेक्षिकतानुकूल सिद्धांत का अनिवार्य फल है। डिरैक समीकरण में यह गुण है कि उससे स्वयं ही इलेक्ट्रान का चुंबकीय घूर्ण भी निकल आता है।
समाप्ति-इलेक्ट्रान के गुण-धर्म-वर्णन के लिए डिरैक समीकरण का उपयोग अनिवार्य है। आजकल जितने परीक्षण हुए हैं सबसे परिणाम इस समीकरण के अनुकूल है। दुबारा क्वांटीकरण पर (द्र. क्वांटस यांत्रिकी) यह समीकरण अत्यंत शक्तिशाली हो जाता है।
सं.ग्रं.-इसी विश्वकोश में 'क्वांटम यांत्रिकी' शीर्षक लेख; डब्ल्यू. पाउली तथा ज़ीमन, फ़रहांडलिंगन मार्टिनस नाइहोफ़, पृ. ३१-४३ (१९३५); हांडबुख़ डर फ़िज़ीक, द्वितीय श्रेणी, खंड २४, पृ. २५१-२७२ (एडवर्ड ब्रदर्स, मिशिगन, द्वारा पुनर्मुद्रित, १९४७)। (वा.)
श्