आतानक विश्लेषण (टेंसर ऐनालिसिस) का मुख्य उद्देश्य ऐसे नियमों की रचना और अध्ययन है, जो साधारणतया सहचर (कोवैरिऐंट) रहते हैं, अर्थात् यदि हम नियामकों की एक संहति से दूसरी में जाएं तो ए नियम ज्यों के त्यों बने रहते हैं। इसीलिए अवकल ज्यामिति के लिए यह विषय महत्वपूर्ण है।

मान लीजिए, एक त्रिविस्तारी अवकाश (स्पेस) अ३है जिसके प्रत्येक बिंदु पा के नियामक तीन वास्तविक राशियों य१य२ य३ पर आश्रित हैं। मान लीजिए, पा के निकट ही फा एक दूसरा बिंदु है जिसके नियामक (य१+ताय१य२+ताय२य३+ताय३) हैं, तो इस अवकल कुलक (सेट ऑव डिफ़रेंशियल्स)

ताय१ ताय२ ताय३

मान लीजिए, हम य¢१, य२, य३,को एक दूसरी नियामक पद्धति य¢१ य¢२ य¢३ में परिवर्तित करते हैं, जो ऐसी है कि पहले नियामक दूसरे नियामकों के सतत फलन हैं। इसके अतिरिक्त अवकल गुणक

तय१ तय२ तय३ तय१ तय२

तय१'' तय२'' तय३'' तय्ा१'' तय३''

भी सतत हैं (जहाँ त º ¶ )और जैकोबियन

त (य१, य२, य३,)

त (य१¢, य२¢, य३¢,)

ताय१¢ =ताय1/ताय३ * ताय२

अब मान लीजिए, का१, का२, का३ तीन राशियाँ हैं, तो इनका रूपांतर इस के सूत्रों से होगा:

ताय१'=ताय₁/ताय_३ * ताय_२

तो इस राशि कुलक का१, का२, का३ को पदवी एक के प्रतिचल आतानक (कंट्रावैरिऐंट टेंसर ऑव रैंक वन) कहेंगे और राशियाँ का१, का२, का३, उक्त आतानक के ३ संघटक कहलाएँगी। साधारणतया आतानकों में उच्च प्रत्यय लगाए जाते हैं

इसके अतिरिक्त, यदि का१, का२, का३, तीन राशियाँ हों, जिनके पविर्तनसूत्र इस प्रकार के हों:

ताय२'=ताय3/ताय_३ ,* ताय_२

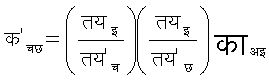
इस प्रकार, यदि स२ राशियाँ काचछ हों, जिनका परिवर्तनसूत्र

हो तो वे भी एक सहचल का सृजन करती हैं और जो राशियाँ काचछ हों, जिनका परिवर्तनसूत्र

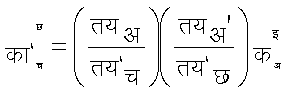
हो,तो वह पदवी २ के एक प्रतिचल का सृजन करती हैं। स्पष्ट है कि हम इन परिभाषाओं का किसी भी पदवी तक विस्तार कर सकते हैं। पदवी. के आतानक को अदिश भी कहते हैं। यह य का एकाकी फलन होता है, जो नियामकों के किसी भी परितर्वन फ'= फ के लिए निश्चल (इन्वैरिएँट) रहता है।

सं.ग्रं.-एल.पी.आइज़ेनहार्ट : कंटिन्युअस ग्रूप्स ऑव ट्रैंसफॉर्मेशंस (१९३३); ओ.वेब्लेन : इन्वैरिएँटस ऑव क्वाड्रैटिक डिफ़रेंशियल फ़ार्म्स (१९२७); ए.डी. माइकेल : मैट्रिक्स ऐंड टेंसर कैलक्युलस विद ऐप्लिकेशन्स टु मेकैनिक्स, इलैस्टिसिटी ऐंड एअरोनॉटिक्स (१९४६)। (ब्र.मो.)