
अवकल समीकरण (डिफरेंशियल ईक्वेशंस) उन संबंधों को कहते हैं जिनमें स्वतंत्र चल तथा अज्ञात परतंत्र चल के साथ साथ उस परतंत्र चल के एक या अधिक अवकल गुणांक (डिफ़रेंशियल कोइफ़िशेंट्स) हों। यदि परतंत्र चल एक तथा स्वतंत्र चल भी एक ही हो तो संबंध को साधारण (ऑर्डिनरी) अवकल समीकरण कहते हैं। जब परतंत्र चल तो एक परंतु स्वतंत्र चल अनेक हों तो परतंत्र चल के खंडावकल गुणक होते हैं। जब ये उपस्थित रहते हैं तब संबंध को आंशिक (पार्शियल) अवकल समीकरण कहते हैं। परतंत्र चल को स्वतंत्र चल के पर्दो में व्यंजित करने को अवकल समीकरण का हल करना कहा जाता है।
यदि अवकल समीकरण में च वीं कक्षा का (ऑर्डर) अवकल गुणक हो और अधिक का नहीं, तो अवकल समीकरण च वीं कक्षा का कहलाता है। उच्चतम कक्षा के अवकल गुणक का घात (पॉवर) ही अवकल समीकरण का घात कहलाता है। घात ज्ञात करने के पहले समीकरण को भिन्न तथा करणी चिंहों से इस प्रकार मुक्त कर लेना चाहिए कि उसमें अवकल गुणकों पर कोई भिन्नात्मक घात न हो। उदाहरणत :

में अवकल समीकरण (१) पहली कक्षा तथा एक घात का है; (२) की कक्षा दो परंतु घात एक है; (३)की कक्षा चार तथा घात पाँच है; और (४) की कक्षा दो और घात तीन (जैसा भिन्न और करणी चिहों से मुक्त करने पर स्पष्ट हो जाता है)।
यदि च१, च२, च३,..., चम स्वेच्छ अचल हों और
फ (य,र,च१,च२,च३,..., ...,चम)=० (५)
में फ चलों य, र का कोई फलन, तो इसे म बार अवकलन करने से म अन्य समीकरण प्राप्त होते हैं। इन म+१ समीकरणों द्वारा सभी अचलों के लुप्तीकरण से संबंध
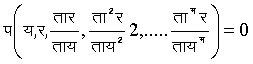 (६)
(६)
प्राप्त होता है। यह (५) का अवकल समीकरण है, जो म वीं कक्षा का है। संबंध (५) को अवकल समीकरण (६) का पूर्ण पूर्वग कहते हैं। इसे व्यापक अनुकल या व्यापक हल भी कहते हैं। यह आवश्यक नहीं कि पूर्वग य का स्पष्ट फलन हो। वास्तव में य, र के वे सभी संबंध अवकल समीकरण के अवकल कहलाते हैं जिनसे प्राप्त र तथा र के अन्य अवकल गुणकों के मान अवकल समीकरण को संतुष्ट कर सकते हैं। (५) और (६) से यह स्पष्ट है कि पूर्ण पूर्वग में स्वेच्छ अचलों की संख्या अवकल समीकरण की कक्षा के बराबर होती है। यदि पूर्ण पूर्वग में कुछ या सब अचलों को विशेष मान दे दिए जाएँ तो वह विशिष्ट अनुकल कहलाता है।
यदि संबंध (५) का लेखाचित्र खींचा जाए तो स्वेच्छ अचलों को भिन्न-भिन्न मान देने से अनंत वक्र मिलेंगे। वक्रों के इस समुदाय में एक ऐसी विशेषता है जो इसके प्रत्येक वक्र में पाई जाती है और जो स्वंतत्र अचलों पर निर्भर नहीं है। इसी विशेषता को अवकल समीकरण प्रकट करता है और वक्रों का यह समुदाय अवकल समीकरण का वक्रपरिवार कहलाता है।
अवकल समीकरण का अनुकलन सरल नहीं है। अभी तक प्रथम कक्षा के वे अवकल समीकरण भी पूर्ण रूप से हल नहीं हो पाए हैं। कुछ अवस्थाओं में अनुकलन संभव हैं, जिनका ज्ञान इस विषय की भिन्न-भिन्न पुस्तकों से प्राप्त हो सकता है। अनुकलन करने की विधियाँ सांकेतिक रूप में यहाँ दी जाती हैं।
प्रथम कक्षा और एक घात के अवकल समीकरण-इनके हल करने की बहुत विधियाँ हैं। उदाहरणत :
(अ) चलों को पृथक् करके अनुकलन करते हैं; उदाहरणत:, अवकल समीकरण (१) को निम्नांकित प्रकार से लिख सकते हैं:
फ (र) तार=प (य) ताय।
अत: अनुकलन करके

इसमें र=पय लिखने से चल पृथक् हो जाते हैं; फिर (अ) की तरह अनुकलन कर लेते हैं।
(इ) एकघात अवकल समीकरण--जब अवकल समीकरण में र तथा र के सभी अवकल गुणक एक घात के हों तो वह एकघात अवकल समीकरण कहलाता है। पहली कक्षा के एकघात समीकरणों का उदाहरण
तार/ताय+प (य) र=ब (य)
है। इसको हल करने के लिए दोनों पक्षों को
ईòप(स) ता य
से गुणा कर देते हैं जहाँ ई (ºe) प्राकृतिक लघुगणकों का आधार है, इससे बायां पक्ष र ईòप(य) ताय का अवकल गुणक हो जाता है। दोनों पक्षों का अनुकलन करने से
र ईòप(स) ता य = ò ब(य)ईòप(य) ता य ताय+च
प्राप्त होता है जो अवकल समीकरण का पूर्ण पूर्वग है।
(ई) शुद्ध अवकल समीकरण-ऊपर बता चुके हैं कि पूर्वग से स्वेच्छ अचलों को हटा देने से अवकल समीकरण प्राप्त होता है। यदि स्वेच्छ अचलों का लुप्तीकरण गुणा, भाग तथा अन्य बीजगणितीय क्रियाओं के बिना ही केवल अवकलन द्वारा हो जाए तो इस प्रकार प्राप्त समीकरण को शुद्ध अवकल समीकरण कहते हैं। कभी-कभी अवकल समीकरण किसी फलन से गुणा करने पर भी शुद्ध अवकल सुमीकरण बन जाता है। ऐसे गुणक को अनुकलन गुणक कहते हैं। जैस (इ) में ईòप(य) ताय अनुकलन गुणक है। प्रथम कक्षा का अवकल समीकरण
फ (य, र) ता र+प(य, र) त१ य=०
![]()
यहाँ तफ/तय का अर्थ है फ (य, र) का य के अनुसार आंशिक अवकल गुणक।
कुछ अवकल समीकरण ऐसे होते हैं जो वैसे तो उपर्युक्त रूपों में नहीं होते परंतु स्वतंत्र और परतंत्र चलों की उचित स्थानापत्ति (सब्स्टिट्यूशन) से इन रूपों में लाए जा सकते हैं तथा उनकी तरह हल किए जा सकते हैं। इस विधि को स्वतंत्र चल परिवर्तन तथा परतंत्र चल परिवर्तन कहते हैं।
प्रथम कक्षा परंतु एक से उच्च घात के अवकल समीकरण०प्रथम कक्षा परंतु एक से उच्च घात समीकरण से तार/ताय का मान बीजगणितीय रीतियों से निकालकर उपर्युक्त विधियों से हल कर लेते हैं। इसके हल में स्वेच्छ अचल होता तो एक है, परंतु उसका घात अवकल गुणक के घात के बराबर हाता है।
अवकल समीकरण के वक्रपरिवार का अवगुंठन (एनवेलप) उस परिवार के प्रत्येक सदस्य को स्पर्श करता है। अत: स्पर्शबिंदु के नियामक तथा संगत सदस्य के तार/ताय का मान ही उस बिंदु पर अवगुंठन के तार/ताय का मान होत है। अत: अवगठन का समीकरण अवकल समीकरण को संतुष्ट करता है। अवगठन इस परिवार का सदस्य नहीं है, न पूर्वग में स्वेच्छ अचलों को विशेष मान देने से ही प्राप्त होता है। अत: यह हल अपूर्व अनुकल (सिंगुलर सोल्यूशन) कहलाता है, जो वास्तव में परिवार के अवगठन का समीकरण होता है।
एक से उच्च कक्षा के एकघात अवकल समीकरण-यदि एकघात अवकल समीकरण
![]()
पर विचार करें तो स्थानापत्ति से यह स्पष्ट है कि यदि र=फ१(य) इसका एक हल है तो र=क१फ१(य), भी हल होगा जहाँ क१ कोई स्वेच्छ अचल है। यदि र=फ१(य), र=फ२(य), र=फ३(य),..., र=फच (य) सभी हल हों तो
र=क१फ१(य)+क२फ२(य)+...+कचफच (य) (८)
भी (७) का हल होगा जहाँ क१, क२,..., कच स्वेच्छ अचल हैं। यदि ये सब फलन स्वतंत्र हैं तो मान (८) अवकल समीकरण (७) का पूर्ण पूर्वग होगा, क्योंकि इसमें स्वेच्छ अचलों की संख्या अवकल समीकरण की कक्षा के बराबर है।
समीकरण
श्
![]()
समीकरण (७) की सहायता से हल होता है। यदि फ१, फ२,..., फच अवकल समीकरण(७) के हल हों और फा (य) समीकरण (९) का एक विशिष्ट हल हो तो
र=क१फ१(य)+क२फ२(य)+...+कचफच(य)+फा (य) (१०)
समीकरण (९) का पूर्ण पूर्वग होगा।
अवकल गुणकों के गुणक (कोइफिशेंट) यदि अचल हों, अर्थात् समीकरण निम्नांकित प्रकार का हो
श्
![]()
जिसमें क० क१..., कच अचल हैं तो इसमें र=ई य लिखने से जहाँ ई (ºe) प्राकृतिक लघुगुणकों का आधार है, संबंध
![]()
प्राप्त होता है। इस समीकरण को हल करने से म के च मान प्राप्त होते हैं । यदि वे म१, म९,..., मच हों तो संबंध
र=ख१ ईम१य + ख२ इर्म२य +...+ खच ईम्ाचय (१३)
समीकरण (११) को संतुष्ट करता है। मान (१३) अवकल समीकरण (११) का पूर्ण पूर्वग है। समीकरण (१२) को अवकल समीकरण (७) का सहायक समीकरण (ऑक्ज़िलियरी इक्वेशन) कहते हैं। समीकरण
![]()
का हल संबंध (१३) के दाएँ पक्ष में य का एक विशेष फलन जोड़ने से प्राप्त होता है, जिसे समीकरण (१४) का विशिष्ट अनुकलन कहते हैं तथा (१३) को अवकल समीकरण (१४) का पूरक फलन कहते हैं।
विज्ञान में अधिकर द्वितीय कक्षा के अवकल समीकरणों का ही प्रयोग होता है। इनके हल बहुत महत्व रखते हैं। एक-एक समीकरण पर बड़े-बड़े ग्रंथ लिखे जा चुके हैं, जैसे जीजेंडर के अवकल समीकरण
तथा बेसल के अवकल समीकरण
श्रेणी में हल-यदि हम अवकल समीकरण (२) का हल एक अनंत परंतु संसृत श्रेणी
र=यच(क०+क१य+क२य२...) (१५)
मान लें, तथा इससे प्राप्त तार/ताय, ता२र/ताय२ के हल मान अवकल समीकरण में स्थानापत्ति करें, तो सरल करने पर तादात्म्य
(१-य३) [-क०च(च-१)यच्ा-२+क१(च+१)च यच-१+क२(च+२) (च+१) यच+...]
-२य (क०च यच-१+क१ (च+१) यच+क२(च+२)यच+१+...]
+२ (क०यच+क१च+१+क२यच+२+...]=०
प्राप्त होता है।
इसको सरल करके य के प्रत्येक घात के गुणक को शून्य बराबर लिखने से समीकरण
क०च(च-१)=०
क१(च+१)च=०
क२(च+२) (च+१)-क०च(च-१)-२क०च=० (१६)
प्राप्त होते हैं। समीकरण (१६) से च=१ या ०; अन्य समीकरणों से क१, क२, क३,... के मान च के पदों में ज्ञात कर लेते हैं। इनमें च के प्रत्येक मान को स्थानापन्न करके दो फलन
रा=य, री=१-य२-1/3य४-1/4य६...
प्राप्त होते हैं जिनसे (२)का पूर्ण पूर्वग
र=क०रा+ख०री
प्राप्त होता है। समीकरण (१६) समीकरण (२) का घातीय समीकरण (इंडिशियल इंक्वेशन) कहलता है। इसी प्रकार अन्य समीकरण भी हल किए जाते हैं। साधारणत: घातीय समीकरण के मूलों की संख्या अवकल समीकरणों की कक्षा के बराबर होती है।
युगपत अवकल समीकरण-यदि परंतत्र चल एक से अधिक हों तो पूर्वग ज्ञात करने के लिए साधारणत: उतने ही अवकल समीकरण होने चाहिए लितने परंतत्र चल। जैसे

यहाँ ल और र परतंत्र चल हैं। इन समीकरणों द्वारा ल का लुप्तीकरण करने पर एक साधारण अवकल समीकरण प्राप्त होता है, जिसे हल करके र का मान प्राप्त करते हैं। फिर दिए हुए समीकरणों में र की स्थानापत्ति करके या तो ल का मान ज्ञात हो जाता है, अन्यथा ऐसा अवकल समीकरण प्राप्त होता है जिसे हल करके ल का मान ज्ञात कर सकते हैं।
यदि परंतत्र चल दो हों और केवल एक ही संबंध ज्ञात हो तो पूर्वग प्रत्येक अवस्था में ज्ञात नहीं हो सकता।
प्रथम कक्षा और एक घात का समीकरण निम्नांकिंत रूप में लिखा जा सकता है :
प (य, र, ल) ताय+फ (य, र, ल) तार+ब (य, र, ल) ताल=०।
इसे तभी हल कर सकते हैं जब फलन प, फ, ब समीकरण

को संतुष्ट करें। इसे अनुकलन की शर्त (कंडिशन ऑव इंटीग्रेबिलिटी) कहते हैं।
यदि प, फ ब यह शर्त पूरी नहीं करते तो इसे हल करने के हेतु हम य, र, ल में दूसरा स्वेच्छ संबंध मान लेते हैं, जिसकी सहायता से पूर्वोक्त विधि या अन्य विधियों से समीकरण को हल करते हैं।
आंशिक अवकल समीकरण-ये समीकरण दो प्रकार से प्राप्त होते हैं। पूर्वग को स्वेच्छ अचलों से मुक्त करके या इसे स्वेच्छ फलन से मुक्त करके।
यदि ल परतंत्र चल तथा य, र स्वतंत्र चल हों और
प (य, र, ल, क, ख) =० (१७)
में फ चलों य, र ल को कोई फलन हो ता इस संबंध तथा संबंध तप/तय =० , तप/तर =० से क, ख का लोप करके आंशिक अवकल समीकरण
फ (य, र, ल, पा, फा) =० (१८)
प्राप्त होता है। यहाँ
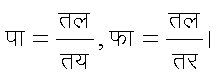 ।
।
संबंध (१७) समीकरण (१८) का पूर्ण अनुकल कहलाता है।
इस प्रकार यदि
व (श, ष) =० (१९)
जहाँ श, ष स्वतंत्र चल य, र, ल के ज्ञात फलन हैं और व चलों श, ष का कोई स्वेच्छ फलन है और यदि (१९) का य, र के अनुसार क्रमश: आंशिक अवकलन करके तव/तश, तव/तष का लोप करें तो प्राप्त आंशिक अवकल समीकरण का रूप
पी पा+फी फा=ब (२०)
हो जाता है जहाँ पी, फी, और ब चलों य, र, ल के फलन हैं।
(१९) को (२०) का पूर्ण अनुकल कहते हैं। क, ख को विशेष मान देने से या व को विशेष रूप देने से प्राप्त संबंधों को विशिष्ट अनुकल कहते हैं।
यदि (१७) को लेखाचित्र खींचें तो तलों का एक परिवार मिलता है। इस तलपरिवार का अवगुंठन भी आंशिक अवकल समीकरण (१८) को संतुष्ट करता है। परंतु यह हल (१७) से प्राप्त नहीं होता। अत: इसे अपूर्व अनुकल कहते हैं।
यदि (१७) में ख को क का कोई स्वेच्छ फलन फ (क) मान लें तो हम देखते हैं कि
प [य, र, ल; क, फ (क)] =0
अब यदि हम इसका लेखाचित्र क के भिन्न मानों के लिए खींचे तो तलों का एक परिवार मिलता है। इस परिवार के आसन्न तलों के कटान वक्रों को लाक्षणिक (कैरेक्टरिस्टिक) कहते हैं। इन वक्रों का अवगुंठन भी अवकल समीकरण (१४) को संतुष्ट करता है। इस अनुकल को व्यापक अनुकल कहते हैं।
प्रयुक्त गणित, भौतिक विज्ञान तथा विज्ञान की अन्य शाखाओं में भौतिक राशियों को समय, स्थान, ताप इत्यादि स्वतंत्र चलों के फलनों में तुरंत प्रकट करना प्राय: कठिन हो जाता है। परंतु हम उनकी वृद्धि की दर तथा उसके अवकल गुणकों में कोई संबंध बहुधा बड़ी सुगमता से पा सकते हैं। इस प्रकार ऐसे अवकल समीकरण प्राप्त होते हैं जिन्हें पूर्वोक्त राशियाँ संतुष्ट करती हैं। इन्हें हल करना उन राशियों का ज्ञान प्राप्त करने के लिए आवश्यक होता है। इसलिए विज्ञान की उन्नति बहुत अंश तक अवकल समीकरण की प्रगति पर निर्भर है।
सं.ग्रं.-गोरखप्रसाद : प्रारंभिक अवकल समीकरण; मरे, प्यागो, फ़ोरसाइथ, बेटमैन, इंस इत्यादि के अवकल समीकरण। (झ.ला.श.)
श्