अवकल ज्यामिति (मापीय) अवकल ज्यामिति में उन तलों और बहुगुणों (मैनीफ़ोल्ड्स) के गुणों क अध्ययन किया जाता है जो अपने किसी अल्पांश (एलिमेंट) के समीप स्थित हों जैसे किसी वक्र अथवा तल के गुणों का अध्ययन , उसके किसी बिंदु के पड़ोस में। मापीय अवकल ज्यमिति का संबंध उन गुणों से है जिनमें नापने की क्रिया निहित हो।

हम किसी वक्र वा की इस प्रकार व्याख्या करते हैं कि वह एक ऐसे बिंदु का बिदुपथ है जिसके निर्देशांक एक ही प्राचल (पैरामीटर) के पदों में व्यक्त हो सकें। ऐसे वक्र के समीकरण इस प्रकार के होंगे:

जिनमें ट प्राचल है। इन समीकरणों से अवकलों (डिफ़रेंशियलों) ताय, ताल, तार, की गणना करके (१) में प्रतिस्थापित करने से इस प्रकार का संबंध प्राप्त होगा:

इसके अनुकूलन से वा के किसी भी चाप का मान निकाला जा सकता है।

जो कोण स्पर्शी और द्विलंब एक नियत दिशा से बनाते हैं उनके परिवर्तन की चाप-दरें (आर्क-रेट) वक्र वा की बिंदु पा पर क्रमानुसार वक्रता और कुटिलता (टॉर्शन) कहलाती हैं और उन्हें ड और ढ से निरूपित किया जाता है। किसी भी सरल रेखा की वक्रता और कुटिलता प्रत्येक बिंदु पर शुन्य होती है और किसी भी समतल वक्र की केवल कुटिलता प्रत्येक बिंदु पर शून्य होती है।

वक्र के किसी बिंदु पा पर की वक्रता ड उसके आश्लेषण वृत्त की त्रिज्या का व्युत्क्रम होती है। इसलिए उक्त वृत को बिदु पा का वक्रतावृत्त भी कहते हैं। रशियों ड,ढ ओर द का वक्र से घनिष्ठ संबंध होता है। यदि ड, ढ दिए हों तो वक्र केवल स्थिति और अनुन्यास (ओरियंटेशन) छोड़कर, पूर्ण रूप से निश्चित हो जाता है। जैसे, यदि वक्रता और कुटिलता दोनों प्रत्येक बिंदु पर शून्य हों तो वक्र एक ऋजु रेखा होगा। यदि वक्रता अचर और कुटिलता शून्य हो तो वक्र एक वृत्त होगा। यदि वक्रता और कुटिलता दोनों शून्येतर हो तो एक वर्तुल भ्रमी (सर्क्युलर हेलिक्स) होगा।

किसी तल पृ की परिभषा हम इस प्रकार दे सकते हैं कि वह एक ऐसे बिंदु परिवार का बिंदुपथ होता है जिसमें दो प्राचल हों। यदि प्राचल ष, स हों तो तल के प्राचलीय समीकरण इस प्रकार के होंगे:

इनको वक्रीय निर्देशांक (कर्विलिनियर कोआर्डिनेट्स)भी कहते हैं। किसी तल के इस प्रकार के निरूपण का ढंग पहले पहल गाउस ने निकाला था।

यदि कोई वक्र वा तल त पर स्थित है तो उसका समीकरण ऐसा होगा:

क्योंकि यदि हम इस समीकरण में से ष के पदों (टर्म्स) में स का मान निकालकर (४) में रख दें तो य, र, ल एक ही प्राचल ष के फलन बन जाएँगे। अत: बिंदु (य,र,ल) का बिंदुपथ एक वक्र हो जाऐगा। वक्र की दिशा ताष/तास पर निर्भर होगी।

यदि पा तल पृ पर कोई बिंदु है तो तल पर पा से होकर जितने भी वक्र खींचे जा सकते हैं, उन सबकी स्पर्शरेखाएँ एक तल पर स्थित होंगी जिसे बिंदु पा का स्पर्श समतल कहते हैं। जो रेखा पा से होकर उक्त समतल पर लंबवत् खींची जाए, वह पृ की, बिंदु पा पर, अभिलंब कहलाती है।

जिस तल का सृजन किसी ऋजुरेखा की गति से होता है, वह ऋजु रेखज तल (रूल्ड सरफ़ेस) कहलाता है। इस प्रकार उक्त तल पर जो अनंत ऋजु रेखाएँ स्थित होती हैं, तल के जनक (जेनेरेटर) कहलाती हैं। यदि तल का स्पर्श समतल एक ही प्राचल पर निर्भर हो तो तल को खोलकर एक समतल पर फैलाया जा सकता है। अत: उसे विकास्य तल (डेवेलपेबुल सरफ़ेस) कहते हैं। शंकु (कोन)और बेलन (सिलिंडर) ऐसे तलों के सरल उदाहरण हैं। वह ऋजुरेखज तल जो विकास्य न हो, विषमतली कहलाता है। जो ऋजुरेखज तल किसी विषमतली वक्र के मुख्य अभिलंबों अथवा द्विलंबों द्वारा होता है, वे विषमतीय होते हैं।

यदि (४) से अवकलों ताय, तार, ताल के मान निकालकर (१) में रख दिए जाएँ तो इस प्रकार का संबंध प्राप्त होगा :

इस समीकरण के दाहिने पक्ष में अवकलों का जो वर्ग व्यंजक है, पृ का प्रथम मूलभूत रूप (फ़ंडामेंटल फ़ार्म) कहलाता है और गुणांक चा, छा, जा तल के प्रथम क्रम (ऑर्डर) के मूलभूत परिमाण (फ़ंडामेंटल मैग्निटयूड्स) कहलाते हैं। इनमें ष, स के प्रति य, र, ल के केवल प्रथम आंशिक अवकलजों (डेरिवेटिव्ज) का समावेश होता है। पृ पर स्थित वक्रों की चाप लंबाइयां, वक्रों के मध्यस्थ कोण और पृ के विभिन्न भागों के क्षेत्रफल, इन सब में केवल चा, छा, जा का ही समावेश होता है।

यदि तल पृ का, पा के अभिलंब से होकर किसी दिशा में खींचे गए समतल द्वारा, काट (सेक्शन) लिया जाए तो उसे अभिलंब काट (नॉर्मल सेक्शन) कहते हैं और यदि इस अभिलंब काट की वक्रता निकाली जाए, तो वह उस दिशा में पा की अभिलंबवक्रता कहलाती है।

ताष/तास की दिशा में बिंदु (ष, स) की अभिलंबवक्रता का सूत्र यह है:

जिसमें दक्षिण पक्ष के व्यंजक के अंश को पृ का द्वितीय मूलभूत रूप कहते हैं और टा, ठा, डा तल के द्वितीय क्रम के मूलभूत परिमाण कहलाते हैं। इनमें य, र, ल के, ष, स के प्रति, द्वितीय क्रम के अवकलजों का समावेश होता है। छह गुणांको चा, छा, जा, टा, ठा, डा में परस्पर तीन स्वतंत्र संबंध होते हैं जिन्हें गाउस और मैनार्डी कोडाज़ी समीकरण कहते हैं। तल सिद्धांत में इन छह गुणांको का उतना ही महत्व है जितना वक्र सिद्धांत में वक्रता और कुटिलता का। यदि ये छह गुणांक ष, स के फलनों के रूप में दिए हों तो स्थिति और अनुन्यास को छोड़कर, तल पूर्ण रूप से निश्चित हो जाता है। वह तल जिसके प्रत्येक बिंदु पर टा, ठा, डा शून्य हों, समतल होता है। वह तल जिसके लिए

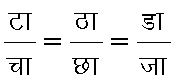
या तो गोला होगा या समतल। किसी बिंदु की अभिलंब-वक्रता ताष/तास पर निर्भर रहती है। यदि यह किसी बिंदु की प्रत्येक दिशा में एक समान हो तो बिंदु को नाभिज (अंबिलिक) कहते हैं। यदि किसी तल का प्रत्येक बिंदु नाभिज हो तो तल पर एक गोला होगा। यदि किसी तल का कोई बिंदु पा नाभिज न हो तो पा पर दो परस्पर लंब दिशाएँ ऐसी होगी जिनकी अभिलंबवक्रताएँ चरम (एक्स्ट्रीमम) होंगी। ये दिशाएँ मुख्य दिशाएँ, और इन दिशाओं की अभिलंबवक्रताएँ मुख्य वक्रताएँ कहलाती हैं। किसी बिंदु की मुख्य वक्रताओं का जोड़ माध्य वक्रता (मीन कर्वेचर) कहलाता है और उसे जा से निरुपित करते है। इसी प्रकार, मुख्य वक्रताओं का गुणनफल गाउसी वक्रता कहलाता है और झा से निरूपित होता है। यदि किसी तल के प्रत्येक बिंदु की माध्य वक्रता शून्य हो तो उसे लघुतमी तल (मिनिमल सर्फ़ेस) कहते हैं। रज्जुज (कैटेनॉयड) और लांबिक सर्पिलज (राइट हेलिकॉयड) लघुतमी तलों के उदाहरण हैं। ऋजुरेखज लघुतमी तल केवल लांबिक सर्पिलज ही होता है और लघुतमी परिक्रमण तल केवल रज्जुज ही होता है। यदि किसी तल के प्रत्येक बिंदु की गाउसी वक्रता शून्य हो तो तल एक छद्मगोला (सूडो-स्फ़ियर) होगा। गाउसी वक्रता की ज्यमितीय परिभाषा इस प्रकार भी दी जा सकती है:

मान लीजिए, पृ का एक छोटा सा भाग प्री है जिसका पर्यत वक्र वा है। एक एकक (यूनिट) त्रिज्या का एक गोला लेकर केंद्र से वा के बिंदुओं पर पृ के अभिलंबों के समांतर रेखाएँ खींचे। ये रेखाएँ गोले के तल को जिन बिंदुओं पर काटती हैं, मान लीजिए, ये वक्र वी का सृजन होता है। जब क्षेत्र प्री सिकुड़कर बिंदु पा से अभिन्न हो जाता है तब अनुपात

वी से समावृत क्षेत्र

वी से समावृत क्षेत्र

की सीमा को बिंदु पा पर पृ की गाउसी वक्रता कहते हैं जिसका सूत्र यह है:

पृ पर स्थित वे वक्र, प्रत्येक बिंदु पर जिनकी दिशाएँ मुख्य दिशाएँ होती हैं, पृ की वक्रतारेखाएँ कहलाती हैं। गोले और समतल को छोड़कर शेष प्रत्येक तल पर वक्रतारेखाओं के दो परिवार होते हैं जो परस्पर लंबवत् काटते हैं। किसी परिक्रमण तल की वक्रतारेखाएँ अक्षांश (लैटीटयूड) रेखाएँ और देशांतर (लांजीट्यूड) रेखाएँ होती हैं। किसी सकेंद्र द्विघाती तल की वक्रतारेखाएँ वे वक्र होती हैं जिनमें वे अपने संनाकियों (कॉन-फ़ोकल्स) को काटती हैं।

यदि पृ पर कोई वक्र वा ऐसा हो कि प्रत्येक बिंदु पर वा की दिशा में अभिलंबवक्रता शून्य हो तो वा को पृ की अनंतस्पर्शी रेखा (ऐसिंटोटिक लाइन) कहते हैं। साधारणतया, प्रत्येक तल पर अनंतस्पर्शी रेखाओं के दो परिवार होते हैं जिनका समीकरण यह होता है:

लांबिक सर्पिलज की अनंतस्पर्शी रेखाएँ उसके जनक और भ्रमी होती हैं। किसी लघुतमी तल पर उसकी अनंतस्पर्शी रेखाएँ एक समकोणीय जाल बनाती है। अनंतस्पर्शी रेखाओं का अध्ययन हम एक अन्य दृष्टिकोण से भी कर सकते हैं। मान लीजिए कि पा, फा तल पृ पर दो समीपस्थ बिंदु हैं। मान लीजिए कि पा से होती हुई, पा और फा के स्पर्श समतलों की प्रतिच्छेंद रेखा के समातंर, रेखा पा बा खींची गई है। जब फा,पा की ओर अग्रसर होता है,तब पा फा और पा बा की दिशाएँ परस्पर संयुग्मी (कॉजुगेट) कहलाती हैं। वक्रों के दो कुलक (सेट्स) जो त पर स्थित हों और जिनके किसी भी बिंदु पर खींचे गए स्पर्शी संयुग्मी हों, एक संयुग्मी जाल का निर्माण करते हैं। जो वक्र संयुग्मी (सेल्फ़-कॉअजुगेट) हो, अनंतस्पर्शी रेखा कहलाता है। यह सिद्ध किया जा सकता है कि वा के किसी भी बिंदु की अनंतस्पर्शी रेखा पृ के उसी बिंदु के द्विलंब से अभिन्न होती है और किसी अनंतस्पर्शी रेखा के किसी बिंदु पर खींची गई स्पर्शी की दिशा वही होती है जो तल के उसी बिंदु पर खींची गई दो नतिपरिवर्तन स्पर्शियों (इनफ़्लेक्शनल टैनजेंट्स) में से एक होती है।

पृ पर, अनंतस्पर्शी रेखाओं और वक्रतारेखाओं के अतिक्ति, एक अन्य महत्वपूर्ण वक्र होता है जिसे अल्पांतरी (जिओडेसिक) कहते हैं। पृ के प्रत्येक बिंदु पा से होकर, और प्रत्येक दिशा में, एक वक्र ऐसा होता है जिसका पा वाला आश्लेषण समतल, पृ के बिंदु पा पर खींचे गए अभिलंब, से होकर जाता है। अत: उक्त वक्र के प्रत्येक बिंदु का मुख्य अभिलंब, उस बिंदु पर खींचे गए पृ के अभिलंब से अभिन्न होता है। ऐसे वक्र को अल्पांतरी कहते हैं। अल्पांतरी तल के किन्हीं दो बिंदुओं के मध्ययस्थ सबसे छोटा मार्ग अल्पांतरी होता है। किसी तल के अल्पांतरियों के अवकल समीकरण में केवल चा, छा, जा और इनके प्रथम आंशिक अवकलजों का समावेश होता है। किसी गोले के अल्पांतरी बृहत् वृत्त (ग्रेट सर्किल्स) होते हैं। यदि पा, वक्र वा का कोई बिंदु है तो पा का वह अल्पांतरी जो वा के पा पर खींचे गए स्पर्शी की दिशा में खींचा जाए, वक्र वा का, बिंदु पा पर, अल्पांतरी स्पर्शी (जिओडेसिक टैनजेंट) कहलाता है। किसी वक्र के किसी बिंदु पर के अल्पांतरी स्पर्शी की संगत वक्रता को उस विंदु की अल्पांतरी वक्रता कहते हैं। यह सिद्ध किया जा सकता है कि वक्र वा के किसी बिंदु पर पा की अलपांतरी वक्रता बिंदु के उस वक्रता सदिश (कर्वेचर वेक्टर) का विघटित भाग (रिज़ॉल्व्ड पार्ट) होती है जो उस बिंदु के स्पर्शी समतल में स्थित हो। किसी अल्पांतरी की अल्पांतरी वक्रता उसके प्रत्येक बिंदु पर शून्य होती है। विलोमत: यदि किसी वक्र के प्रत्येक बिंदु पर उसकी अल्पांतरी वक्रता शून्य हो तो वक्र स्वयं एक अल्पांतरी होगा।

वक्र वा के किसी बिंदु पा के अल्पांतरी स्पर्शी की कुटिलता उस बिंदु पर वक्र की कुटिलता कहलाती है। जितने वक्र एक दूसरे को पा पर स्पर्श करते हैं, उन सबकी अल्पांतरी कुटिलता एक सी होती है। किसी भी तल पृ के प्रत्येक बिंदु पा पर दो दिशाएँ होती हैं जिनमें अल्पांतरी कुटिलता चरम होती है। पृ पर स्थित वे वक्र अल्पांतरी कुटिलता रेखाएँ (लाइन्स ऑव जिओडेसिक टॉर्शन) कहलाते हैं। जिनके प्रत्येक बिंदु पर खींचा गया स्पर्शी चरम अल्पांतरी कुटिलता की दिशा में होता है। किसी बिंदु पर अल्पांतरी कुटिलता रेखा की दिशा में दो मुख्य वक्रताएँ होती हैं, जिनके माध्य को उस बिंदु की अभिलंब वक्रता (नॉर्मल कर्वेचर) कहते हैं। पृ पर वे वक्र लक्षण रेखाएँ (कैरिक्टरस्टिक लाइन्स) कहलाते हैं जिनके प्रत्येक बिंदु का स्पर्शी उस दिशा में होता है जिस दिशा में अल्पांपरी कुटिलता और अभिलंब वक्रता का अनुपात चरम हो। किसी तल पर स्थित वे वक्र जिनका समीकरण

हो, मोघ रेखाएँ (नल लाइन्स) कहलाती हैं। किसी तल पर स्थित वक्रों के ये पांच परिवार--मोघ रेखाएँ, अनंतस्पर्शी रेखाएँ, वक्रता रेखाएँ, अल्पांतरी कुटिलता रेखाएँ और लक्षण रेखाएँ-एक बंद संहति (क्लोज्ड सिस्टम) का निर्माण करते हैं। इसका अर्थ यह है कि यदि कोई भी दो समीकरण इस रूप में लिए जाएँ:

और इनके जैकोबियनों को शून्य के बराबर रखा जाए तो उपर्युक्त पाँच संहतियों के अतिरिक्त और कोई संहति प्राप्त नहीं होगी।

किंतु शास्त्रीय अवकल ज्यामिति की भाँति यह मानना आवश्यक नहीं है कि कोई तल यूक्लिडीय अवकाश में ही स्थित होगा।

आधुनिक दृष्टिकोण में किसी बिंदु को स संख्याओं

का क्रमित कुलक (आर्डर्ड सेट) माना जाता है। इस बिंदु से इसके समीपस्थ बिंदु

की दूरी ताद के लिए सूत्र यह है:

में निन्मलिखित मापज प्राप्त होता है:

रीमानीय ज्यामिति का अध्ययन प्रदिश कलन (टेन्सर कैल्क्युलस) की सहायता के किया जाता है। पिछले कतिपय दशकों में रीमानीय ज्यामिति के कई सार्वीकरण (जेनरलाइज़ेशन) निकल आए हैं। इनमें से एक महत्वपूर्ण सार्वीकरण फ़िन्स्लर ज्यामिति अथवा सार्वमापज ज्यामिति (ज्योमेट्री ऑव दि जेनरल मेट्रिक) है जिसमें रीमानीय मापज का स्थान निर्देशांकों और अवकलों का एक अधिक सार्विक फलन फा (य,ताय) ले लेता है।

श्