अनंत श्रेणियाँ एक ऐसी श्रेणी, जिसके पदों की संख्या परिमित न हो, अनंत श्रेणी (इनफिनिट सीरीज) कहलाती है। जैसे-
![]()
एक अनंत श्रेणी है। अनंत श्रेणियाँ परिमित संख्याओं के बराबर होती हैं कि नहीं, और यदि होती है तो अनंत श्रेणियों के साथ जोड़ने, घटाने, गुणन तथा विभाजन आदि की क्रियाएँ किस प्रकार की जा सकती है और अनंत श्रेणियों का क्या महत्व एवं उपयोग है, इन प्रश्नों के समूचित उत्तर देने के लिए हमें गणित के कुछ संकेतों तथा विशेष धारणाओं की आवश्यकता होगी। इनका पहले उल्लेख कर देना ठीक है।
अनुक्रम-गिनती गिनने के क्रम में जो संख्याएँ आती हैं, जैसे १,२,३,..., उनको प्राकृतिक संख्याएँ कहते हैं। प्राकृतिक संख्याओं के समुदाय में कोई अंतिम अथवा सबसे बड़ी संख्या नहीं है, क्योकि किसी भी प्राकृतिक संख्या में १ जोड़ने से पहली से बड़ी एक दूसरी प्राकृतिक संख्या प्राप्त की जा सकती है। अत: प्राकृतिक संख्याओं की संख्या परिमित नहीं है; दूसरे शब्दों में, उनकी संख्या अनंत है। गिनने के क्रम में क्रमागत संख्याओं का परिमाण भी पूर्वागत संख्याओं के परिमाण से अधिक होता जाता है और उनके परिमाण के इस प्रकार बढ़ने के प्रक्रम का कहीं अंत नहीं है। इस परिस्थिति को यह कहकर व्यक्त किया जाता है कि 'प्राकृतिक संख्याओं का परिमाण अनंत की ओर बढ़ता जाता है।' अनंत का प्रतीक ¥ है। एक अनिर्धारित प्राकृतिक संख्या को हम अक्षर प से व्यक्त करेंगे। यदि प का मान इस तरह परिवर्तित हो रहा हो तो कि वह किसी भी प्राकृतिक संख्या से अधिक हो सकता है तो हम कहते हैं कि 'प अनंत की ओर अग्रसर है।' प्रतीकों में इसे प®¥ से व्यक्त करते हैं (द्र. सीमा तथा अनंत)। |प| से किसी भी संख्या प का निरपेक्ष मान व्यक्त किया जाता है जैसे |-२|=|२| =|२|। यदि प का मान इस तरह परिवर्तित हो रहा हो कि वह किसी भी ऋण संख्या से कम हो सकता है तो हम कहते हैं कि प®- ¥।-- ¥<ल<¥ का अर्थ है कि ल एक परिमित संख्या है।
यदि संख्याओं (वास्तविक या संकर) का एक समूह इस प्रकार नियोजित हो कि प्रत्येक प्राकृतिक संख्या उस समूह की एक, और एक ही, संख्या की संगति में लगाई जा सके तो संख्याओं के उस समूह को संख्या-अनुक्रम या केवल अनुक्रम (सीक्वेंस) कहते हैं जैसे १,१/२,१/३.., १/प,... एक अनुक्रम है। इस अनुक्रम का पवाँ पद १/प है। क१,क२,क३,...,क,... एक समान्य अनुक्रम है जिसका पवाँ पद क प है। संक्षेप में, इसको संकेत {क}१¥ अथवा {कप} या केवल कप से व्यक्त करते हैं। अनुक्रम के लिए यह आवश्यक नहीं है कि उसका पवाँ पद सूत्र रूप में लिखा जा सके; पर यह आवश्यक है कि उसका प्रत्येक पद ज्ञेय हो। अभाज्य संख्याओं से एक अनुक्रम बनता है, किंतु पवीं अभाज्य संख्या को सूत्र रूप में नहीं लिखा जा सकता। अनुक्रम में एक ही संख्या बार-बार भी आ सकती है; जैसे, १, २, १, २, १, २,... एक अनुक्रम है। कप®० का अर्थ है कि कप ्ह्रासमान है, तथ जब प®¥ तो इसकी सीमा ० है।
अनंत श्रेणियाँ, उनका अभिसरण तथा अपसरण-यदि क१,...क२....,क३... कोई अनुक्रम हो तो, जैसा ऊपर बताया गया है, क१+क२+...+कप+... को अनंत श्रेणी कहते हैं। इस अनंत श्रेणी का सामान्य पद अथवा पवाँ पद कपहै। संक्षेप में इस श्रेणी को इस प्रकार लिखते है:
![]()
यदि कुछ दी हुई संख्याओं की संख्या परिमित हो तो उनका योगफल भी एक परिमित संख्या होती है, पर अनंत श्रेणियों के योगफल का क्या अर्थ है? कुछ अनंत श्रेणियों का भी योगफल अवश्य होता है और उनके योगफल निकालने की विधि इस प्रकार है। यदि किसी अनंत श्रेणी के प्रथम प पदों का योगफल जप से व्यक्त करें, अर्थात्
जप=क१+क२+...+कप
![]()
तो ज१, ज२,... जप,... एक अनुक्रम बन जाता है। यदि प के ¥ की ओर अग्रसर होने पर अनुक्रम जप की सीमा एक परिमित संख्या ज है, अर्थात् यदि
![]()
तो ऐसी अनंत श्रेणी को अभिसारी श्रेणी (कॉनवर्जेट सीरीज) कहते हैं और उसका योगफल संख्या ज के बराबर माना जाता है। ऐसी श्रेणियाँ जो अभिसारी नहीं होतीं अनभिसारी अथवा अपसारी (नॉन-कॉनवर्जेट) होती हैं। जैसे
अपसारी श्रेणियाँ दो प्रकार की होती हैं। यदि जप,®±¥, तो श्रेणी पूणर् अपसारी होती है और यदि जप का मान दो संख्याओं (परिमित अथवा अनंत) के बीच दोलित होता रहता है तो श्रेणी प्रदोली (ऑसिलेटरों) कहलाती है। १-१+१-१+१-... प्रदोली श्रेणी है।
जैसा हम आगे चलकर देखेंगे, अभिसारी श्रेणियों के साथ ही गणित की प्रधान क्रियाएँ संभव हैं। अत: किसी दी हुई अनंत श्रेणी के संबंध में सर्वप्रथम यह जानना आवश्यक हो जाता है कि वह अभिसारी है या नहीं। इसके लिए एक आवश्यक और पर्याप्त प्रतिबंध यह है कि सीमा (जप- जफ)=०, जब एक दूसरे से स्वतंत्र रहकर प®¥, फ®¥,यह प्रतिबंध व्यवहार में बहुत लाभकर नहीं सिद्ध होता, किंतु इसके आधार पर कई उपयोगी निष्कर्ष निकाले जा सकते हैं; जैसे प्रत्येक अभिसारी श्रेणी के लिए यह आवश्यक है कि कप®०। इस परीक्षा के अनुसार S कोज्या (१/प) अभिसारी श्रेणी नहीं है।
धन श्रेणियाँ--ऐसी श्रेणी जिसके सभी पद धन संख्याएँ हों धन श्रेणी कहलाती है। यदि न एक से बड़ी कोई संख्या है तो श्रेणी
![]()
अभिसारी
होती है और
यदि न£१
तो श्रेणी अपसारी
होती है। इस प्रकार
![]() श्रेणी
अभिसारी है। इसका
योगफल
=१/६p2
जहाँ
p = ३.१४...।
श्रेणी
अभिसारी है। इसका
योगफल
=१/६p2
जहाँ
p = ३.१४...। ![]() अपसारी
है। धन श्रेणियों
के अभिसरण तथा
अपसरण की कुछ
परीक्षाएँ नीचे
दी जाती हैं। जिन
श्रेणियों का उल्लेख
यहाँ होगा वे
सभी धन श्रेणियाँ
हैं।
अपसारी
है। धन श्रेणियों
के अभिसरण तथा
अपसरण की कुछ
परीक्षाएँ नीचे
दी जाती हैं। जिन
श्रेणियों का उल्लेख
यहाँ होगा वे
सभी धन श्रेणियाँ
हैं।
१. यदि कप£गप और Sगप अभिसारी है, तो Sकप भी अभिसारी है। यदि कप³गप और Sगप अपसारी है ता Sकप भी अपसारी है।
२. तुलना परीक्षा-यदि सीमा कप/गप= ल, ०< ल<¥ तो Sकप और Sगप साथ-साथ ही अभिसारी अथवा अपसारी होंगी।
३. अनुपात परीक्षा (दलाँबेर की)-मान लें कि सीमा कप/कप+१= ल। यदि ल>१ तोे Sकप अभिसारी होगी और यदि ल<१ तो अपसारी होगी। यदि ल=१ तो कुछ नहीं कहा जा सकता और नीचे की परीक्षा का प्रयोग करना चाहिए।
४. राबे की परीक्षा-यदि सीमा प (कप/कप=१-१)= ल और ल>१, तो श्रेणी अभिसारी है और यदि ल<१ तो अपसारी है। यदि ल =१ तो नीचे की परीक्षा का उपयोग करना चाहिए।
५. मान लें, जब प®¥, तब
यदि ल>१, तो श्रेणी अभिसारी होगी और यदि ल<१, तो अपसारी होगी।
६. कोशी की मूल परीक्षा-मान लें (कप)१/प®ल। यदि ल<१, तो श्रेणी अभिसारी होगी और यदि ल तो, अपसारी होगी। मूल परीक्षा सिद्धांतत: अनुपातपरीक्षा से अधिक शक्तिपूर्ण है, किंतु व्यवहार में अनुपात परीक्षा अधिक उपयोगी है।
७. समाकल परीक्षा (मैक्लारिन की)-यदि मप ्ह्रासमान हो और कपफº(प), तो
![]()
की सीमा एक संख्या होती है और परिणामस्वरूप समाकल
![]()
एक साथ ही अभिसारी तथा अपसारी होती हैं। इस परीक्षा से यह भी निष्कर्ष निकलता है कि
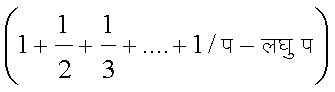
की सीमा एक परिमित संख्या है। इस संख्या को ऑयलर का अचर कहते हैं और इसका मान ०.५७७२१५६६... है।
इनके अतिरिक्त कोशी की संघननपरीक्षा आदि भी हैं। स्थानाभाव से उनका उल्लेख नहीं किया जा रहा है (द्र. संदर्भ ग्रंथ)।
सामान्य श्रेणियाँ और परम अभिसरण-ऐसी श्रेणी कोई दो क्रमिक पद भिन्न के हों (एक+और दूसरा-), एकांतर श्रेणी कहलाती है। यदि कप ®० तो श्रेणी क१-क२+क३-क४... अभिसारी होती है। जैसे १-१/२+1/3-1/4+....अभिसारी है; इसका योग लघु २ है।
यदि धन और ऋण दोनों प्रकार के पदोंवाली श्रेणी S|कप| ऐसी हो कि श्रेणी अभिसारी है, तो यह कहा जाता है कि श्रेणी Sकप परम अभिसारी है। जैसे
१-१/४+1/9-1/16+....परम अभिसारी है; किंतु १-१/२+1/3-1/4+....परम अभिसारी नहीं है। प्रत्येक परम अभिसारी श्रेणी अवश्यमेव अभिसारी होती है, किंतु प्रत्येक अभिसारी श्रेणी परम अभिसारी नहीं होती। १-१/२+1/3-1/4+....अभिसारी है, किंतु परम अभिसारी नहीं है। ऐसी श्रेणी को सप्रतिबंध अभिसारी (कंडिशनली कॉनवर्जेट) कहते हैं। स्पष्ट है कि प्रत्येक अभिसारी धन श्रेणी परम अभिसारी होती है। परम अभिसारी श्रेणी के पदों के क्रम में किसी भी प्रकार का परविर्तन करने से श्रेणी के योगफल में अंतर नहीं पड़ता और वह परम अभिसारी बनी रहती है। इसके विपरीत, सप्रतिबंध अभिसारी श्रेणी के पदों के क्रम में हेर-फेर करने से श्रेणी के आचरण और उसके योग दोनों में अंतर पड़ सकता है। जैस १-१/२+1/3-1/4+....= लघु २, किंतु १-१/२+1/3-1/4+....=लघु २।
जर्मन गणितज्ञ रीमान (१८२६-१८६६) ने यह सिद्ध किया है कि किसी सप्रतिबंध अभिसारी श्रेणी के पदों के क्रम में उचित हेर-फेर करके उसका योग किसी भी संख्या के बराबर किया जा सकता है अथवा उसको हर प्रकार की अपसारी श्रेणी का रूप दिया जा सकता है। परम अभिसारी श्रेणियों तथा सप्रतिबंध अभिसारी श्रेणियों के आचरण के इस मौलिक अंतर का मूल कारण यह है कि परम अभिसारी श्रेणी के धन पदों और ऋण पदों द्वारा अलग-अलग दो अभिसारी श्रेणियाँ बनती हैं तथा इसके विपरी सप्रतिबंध अभिसारी श्रेणी के धनपदों और ऋण-पदों द्वारा अलग-अलग दो अपसारी श्रेणियाँ बनती हैं।
अनंत श्रेणियाँ और प्रधान क्रियाएँ-यदि क=Sकप और ग=Sगप दो अभिसारी श्रेणियाँ हों, तो S(कप±गप) भी अभिसारी होती है और इसका योग = क ±ग, अर्थात् दो अभिसारी श्रेणियाँ के संगत पद जोड़ने और घटाने से बनी श्रेणियाँ भी अभिसारी होती हैं, किंतु गुणनफल के संबंध में वह बात सर्वथा ठीक नहीं है। दो श्रेणियों Sकप और Sकप का गुणनफल श्रेणी

से व्यक्त किया जाता है। परम अभिसरण की धारणा का महत्व दो श्रेणियों के गुणनफल के संबं
ा में अत्यंत स्पष्ट हो जाता है। यदि क=Sकप और ग=Sगप परम अभिसारी हों, तो Sकपगप प्रत्येक दशा में परम अभिसारी होती है तथा इसका योग कग होता है। श्रेणियों Sकप और Sगप का एक विशेष गुणनफल, जिसको कोशी गुणनफल कहते हैं, श्रेणी Sखप से व्यक्त किया जाता है, जिसमें खप= क१गप+क२गप-१+...+कपगप । कोशी गुणनफल के संबंध में कुछ महत्वपूर्ण प्रमेय निम्नलिखित हैं:
१. कोशी प्रमेय-यदि क=Sकप तथा ग=Sगप दो परम अभिसारी श्रेणियाँ हों तो श्रेणी Sखप भी परम अभिसारी होगी और इसका योग कग होगा।
२. मर्टन प्रमेय-यदि क=Sकप परम अभिसारी हो तथा ग=Sगप केवल अभिसारी हो, तो Sखप भी अभिसारी होगी और इसका योग कग होगा।
३. आबेल प्रमेय-यदि क=Sकप और ग=Sगप ये दोनों श्रेणियाँ केवल अभिसारी हों और Sखप भी अभिसारी हो, तो Sखप=कग।
एक समान अभिसरण-अभी तक हमने अचर पदोंवाली श्रेणियों की ही चर्चा की है। मान लीजिए कि श्रेणी
![]()
जिसका प्रत्येक पद कप (य)अंतराल (त,थ) में चर य का फलन है, य के प्रत्येक मान के लिए अभिसारी है। श्रेणी का योगफल क (य) भी य का एक फलन होगा। यदि घ कोई स्वेच्छ धन अचर हो और य१,प२,य३,... अंतराल (त,थ) की संख्याएँ हों, तो इनसे संगत क्रमश: प१,प२,प३,... ऐसी ऐसी प्राकृतिक संख्याएँ होंगी कि |कप (य१)-क (य) S<घ, जहाँ प>प१;|क१ (य२)-क (य२)|<घ, जहाँ प>प२; आदि। यदि य के सभी मानों के लिए एक ही प्राकृतिक संख्या म ऐसी हो कि |क (य)|-क (य) |<घ जब प³म, तो हम कहते हैं कि श्रेणी Sकप (य) अंतराल (त,थ) में एकसमानत: अभिसारी (यूनिफॉर्मली कॉनवर्जेंट) है। स्पष्ट है कि एकसमानत: अभिसारी श्रेणी अवश्यमेव अभिसारी होती है।
एकसमान अभिसरण के लिए कई परीक्षाएँ हैं, किंतु उनमें सबसे सरल और अत्यंत उपयोगी परीक्षा, जिसको जर्मन गणितज्ञ वायर्स्ट्रास ने सिद्ध किया था, इस प्रकार है: यदि Sमप धन अचर पदों की एक ऐसी अभिसारी श्रेणी हो कि य के सभी मानों के लिए कम (य)|£मप, प=१,२,..., तो श्रेणी Sकप (य) एकसमानत अभिसारी होगी। जैसे, श्रेणी १+य+ य२+... अंतराल (०, ग), ०£ग <१, में एकसमानत: अभिसारी है। श्रेणी
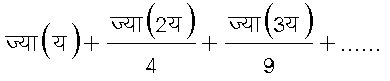
य के सभी मानों के लिए एकसमानत: अभिसारी है। एकसमान अभिसरण का महत्व नीचे के प्रमेयों से स्पष्ट हो जाता है :
१. यदि किसी एकसमानत: अभिसारी श्रेणी का प्रत्येक पर य का सतत फलन हो, तो एक समान अभिसरण के अंतराल में उस श्रेणी का योगफल भी य का सतत फलन होगा।
२. यदि Sकप (य) अंतराल (त,थ)में एकसमानत: अभिसारी हो तथा उसका योग ज (य) हो, तो
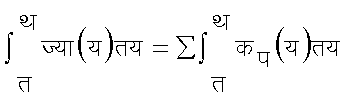
३. यदि ज (य) =Sकप (य) एकसमानत: अभिसारी हो और अवकलित श्रेणी Sकप (य) भी सतत पदों की एकसमानत: अभिसारी श्रेणी हो, तो ज' (य) =Sकप (य)। यहाँ प्रास अवकलन का द्योतक है।
संमिश्रण श्रेणियाँ-ऐसी श्रेणी Sकप जिसका प्रत्येक पद कप=गप+श्रदप, श्र=Ö(-१) (द्र. संमिश्र संख्याएँ), एक संमिश्र संख्या हो, संमिश्र श्रेणी कहलाती है। श्रेणी Sकप तब, और केवल तब, अभिसारी कही जाती है जब दोनों श्रेणियाँ ग=Sगप और द =Sदप अभिसारी हों। Sकप का ग+श्रद योग माना जाता है। यदि
SकqºSÖ(गq२+दq२)
भी अभिसारी हो, तो कहा जाता है कि Sकप परम अभिसारी है। Sकप के परम अभिसरण के लिए यह आवश्यक और पर्याप्त है कि प्रत्येक श्रेणी Sगप और Sदप परम अभिसारी हों। इस प्रकार संमिश्र श्रेणियों का अध्ययन वास्तविक श्रेणियों के अध्ययन में रूपांतरित किया जा सकता है, किंतु स्वतंत्र रूप में उनका अध्ययन पर्याप्त सरल और शिक्षाप्रद होता है।
घात श्रेणियाँ-श्रेणी
जिसमें कप तथा त अचर हैं, और य चर (वास्तविक अथवा संमिश्र), घात श्रेणी कहलाती है। यदि त को शून्य मान लें तो श्रेणी का रूप होगा Sकप यप। घात श्रेणियों से परम अभिसरण तथा एकसमान अभिसरण के बहुत सुंदर उदाहरण मिल सकते हैं। प्रत्येक घात श्रेणी Sकप यप के लिए एक ऐसी अद्वितीय वास्तविक धनसंख्या श्र होती है, ०£श्र£¥, कि य के ऐस सभी मानों के लिए जिनके |य| >त्र, लिए श्रेणी अभिसारी होती है; और उन मानों के लिए श्रेणी अपसारी होती है जिनके लिये |य| >त्र । त्र को श्रेणी की अभिसरण त्रिज्या कहते हैं और वृत्त (अथवा अंतराल) |य|< त्र को श्रेणी का अभिसरण वृत्त (अथवा अंतराल) कहते हैं।
प्रत्येक घात श्रेणी के लिये
त्र = (सीमा |क|१ प)-१।
यदि सीमा |क| ¤ |क१+३| एक निश्यित संख्या है तो त्र का मान उसके बराब हाता है। श्रणियों
१+य+२२य२+३३य३+..., १+य+य२+...,
तथा 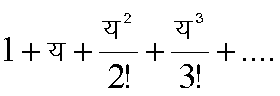
की अभिकरण त्रिज्याएँ क्रमश: ०, १ ओर ¥ हैं। प्रत्येक घात श्रेणी अभिसरण वृत्त के भीतर परम अभिसारी तथा एक समानत: अभिसरी होती है, और उसका योग अभिसरण वृत्त के भीतर एक वैश्लेषिक फलन होता है (द. फलन तथा टेलर श्रेणी)।
अनंत श्रेणियों की संकलनीयता-कुछ ऐसी विधियाँ है जिनकी सहायता से कतिपय अपसारी श्रोणियों के साथ भी योगफल की धारणा का संनिवेश किया जा सकता है। १८ वीं शाताब्दी के जर्मन गणितज्ञ ऑयलर ने अपसारी श्रेणी १-१+१-१+... का योग १/२ माना था और इसका सफलतापूर्वक उपयोग भी किया था। किंतु अपसारी श्रेणियों के उपयोग से प्राय: परस्पर विरोधी निष्कर्ष निकलने लगे। इसलिये कोशी, आबेल आदि ने उपपत्तियों में अपसारी श्रोणियों के प्रयोग को अनुचित बताया। १९वीं शताब्दी में चेज़ारों, बोरेल आदि ने संकलन की ऐसी विधियाँ निकालीं जिनके द्वारा संकलनीय अपसारीे श्रेणियों को भी वही प्रतिष्ठा मिली जो अभिसारी श्रेणियों को मिली थी। स्थानपाभाव से यहाँ केवल चेज़ारों की एक विधि का उल्लेख किया जाता है। यदि जप श्रेणी Sकप के प पदों का जोड़ है तो मान लें
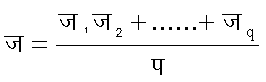
यदि सीमा सप एक निश्चित परिमित संख्या स के बराबर है तो यह कहा जाता है कि श्रेणी Sेंकप चेज़ारी की विधि से संकलनीय है और उसका योगफल स है। इस प्रकार १-१+१-१+...संकलनीय है और इसका योगफल है। प्रत्येक अभिसारी श्रेणी इस विधि से संकलनीय होती है और उसका योगफल बदलता नहीं।
सं. ग्रं.-ब्रॉमविच : ऐन इंट्रोडक्शन टु दि थ्योरी ऑव इनफ़िनिट सीरीज़; क्लॉप : थ्योरी ऐंड ऐप्लिकेशन ऑव इनफ़िनिट सीरीज़; हार्डी : डाइवर्जेट सीरीज़। (उ.ना.सिं.)